Box 3 – Derivation: Formula For Volumetric Flow Rate Through A Flow ...

Trang chủ » Volumetric Flow Formula » Box 3 – Derivation: Formula For Volumetric Flow Rate Through A Flow ...

Có thể bạn quan tâm

Volumetric flow rate (discharge) is the volume of water flowing through a system per unit of time. It is reported in a dimension of volume, or length cubed, over time (for example, liters per minute, or cubic meters per second).

Flow through a homogeneous sand with a hydraulic conductivity of 0.4 cm/s in a rectangular tank is used to derive the formula for volumetric flow rate through a flow net. A diagram of the rectangular tank is shown in Figure Box 3-1. Within the tank, sand fills the volume of a box, with all sides impermeable except where water enters and exits along the dashed black lines through a screen that contains the sand. The box is 33 cm tall, 66 cm long and 50 cm wide (that is, it extends 50 cm “into” the picture). Any cross-section cutting through the box from left to right is identical to every other left-right cross-section, so only one cross section of the box is shown Figure Box 3-1. The water level on the left side is maintained at 50 cm and the water level on the right side is maintained at 44 cm. Flow is from left to right.

Figure showing a rectangular box filled with sand with constant head reservoirs on each side

Figure Box 3-1 – A rectangular box filled with sand with constant head reservoirs on each side.

For this rectangular tank, we do not need to construct a flow net and then apply a formula to determine the volumetric flow rate. Given the simple geometry of this flow tank, the volumetric flow rate can be determined directly by substituting values into Darcy’s Law (Equation Box 3-1) as follows:

Q = −KiA (Box 3-1)

where:

Q = volumetric flow rate (L3/T)
i = hydraulic gradient (dimensionless)
A = area perpendicular to the direction of flow (L2)

\displaystyle Q=-\left ( 0.4\ \frac{\textup{cm}}{\textup{s}} \right )\left ( \frac{44\ \textup{cm}-50\ \textup{cm}}{66\ \textup{cm}} \right )(33\ \textup{cm})(50\ \textup{cm}) = \displaystyle 60\ \frac{\textup{cm}^3}{\textup{s}}

\displaystyle Q=\left (60\ \frac{\textup{cm}^3}{\textup{s}} \right )\left ( 60\ \frac{\textup{s}}{\textup{min}} \right )\left ( \frac{\textup{liter}}{1000\ \textup{cm}^3} \right ) = \displaystyle 3.6\ \frac{\textup{liters}}{\textup{min}}

Although it is easy to use Darcy’s Law to calculate the volumetric flow rate for a simple flow geometry, it is not easy for flow with complex geometry. To determine the volumetric flow rate for the case of complex geometry, it is necessary to either (1) graphically construct a flow net and then apply a formula to calculate the flow rate, or (2) use a numerical computer model to calculate the flow rate. This box addresses the first method and derives the necessary formula. The flow tank is used as an example, but the derived formula is valid for complex cases.

To develop the formula for the flow tank, a graphical flow net is constructed as is shown in Figure Box 3-2. For this simple flow geometry, the equipotential lines are straight and vertical, while the flow lines are straight and horizontal. The two sets of lines intersect at right angles to form squares. Every flow tube carries the same volumetric flow rate. Darcy’s Law can be used to calculate the volumetric flow in an individual flow tube by calculating flow across the width y for a square in the flow net (for example, the one highlighted in black in Figure Box 3-2).

Diagram for deriving equation to determine volumetric flow rate of a flow net

Figure Box 3-2 – Diagram for deriving equation to determine volumetric flow rate of a flow net per unit width into the diagram through one square of a flow net.

The head difference between the equipotential lines in a flow net (Equation Box 3-2) is determined as the quotient of the total head drop across the flow net, H (H = 6 cm in this case), and the number of head drops, nd (nd = 6 in this case, as shown in Figure Box 3-3).

\displaystyle h_{diff}=\textup{contour interval}=\frac{H}{n_{d}} (Box 3-2)

where:

contour interval = head difference between adjacent equipotential lines (L)
H = total head drop across the flow net domain (L)
nd = number of head drops in the flow net (dimensionless)
Figure showing the number of head drops in a flow net

Figure Box 3-3 – Number of head drops in the example flow net.

For this flow net, hdiff = ((6 cm) / (6 head drops)), or 1 cm as is already indicated by the contour line labels in Figure Box 3-2 and Figure Box 3-3.

The volumetric flow rate through one flow tube per unit width normal to the diagram is determined using Darcy’s Law as the product of hydraulic conductivity (K), the gradient (hdiff /x) and the width of the flow tube in the plane of the flow net (Equation Box 3-3).

\displaystyle Q'_{tube}=K\frac{h_{diff}}{x}y (Box 3-3)

where:

Q’tube = volumetric flow rate through one flow tube per unit width perpendicular to the diagram (L2/T)
x = distance between the equipotential lines (L)
y = width of the flow tube in the plane of the flow net (L)

For a square in the flow net (such as the one highlighted in black in Figure Box 3-2), x=y, and the equation can be simplified by canceling y with x, leaving the formula for the flow through a flow tube per unit width into the diagram as shown in Equation Box 3-4.

\displaystyle Q'_{tube}=K\ h_{diff}=K\frac{H}{n_{d}} (Box 3-4 )

For flow nets with more complex geometry, the equipotential lines and flow lines intersect to form curvilinear squares rather than exact squares. In this case, the ratio of x to y can be considered an aspect ratio. For a curvilinear square, the aspect ratio is 1, so that the simplification from Equation Box 3-3 to Equation Box 3-4 is still valid.

Because Q’tube is the same for all flow tubes, the volumetric flow rate through the entire system per unit width perpendicular to the diagram can be obtained by multiplying Q’tube by the number of flow tubes as in Equation Box 3-5.

\displaystyle Q'=Q'_{tube}n_{f}=K\frac{H}{n_{d}}n_{f} (Box 3-5)

where:

nf = number of flow tubes in the flow net
Q’ = volumetric flow rate through the entire system per unit width perpendicular to the diagram (L2/T)

This flow net has 6 head drops (nd = 6) and 3 flow tubes (nf = 3) as shown in Figure Box 3-4.

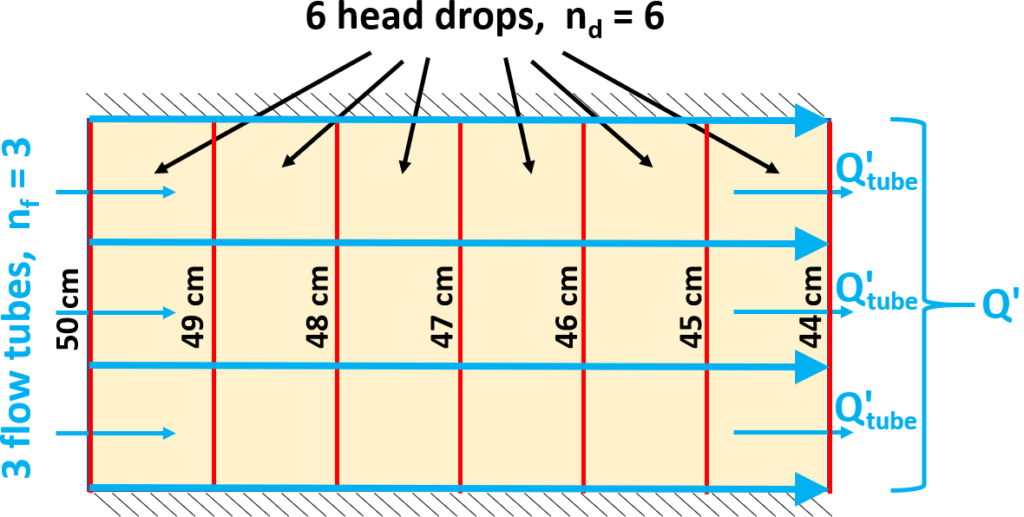
Figure Box 3-4 – Number of flow tubes and head drops in the example flow net.

The parameter Q’ has a dimension of length squared over time, L2/T, because it represents the volumetric discharge rate for one unit-width into the diagram (Equation Box 3-6).

\displaystyle Q'=K\frac{H}{n_{d}}n_{f}=KH\frac{n_{f}}{n_{d}}     :    \displaystyle \frac{\textup{L}}{\textup{T}}\textup{L}\frac{-}{-}    :    \displaystyle \frac{\textup{L}^2}{\textup{T}} (Box 3-6)

where:

− = Indicates a parameter is dimensionless

To calculate the total volumetric flow rate through the box, Qtotal, we multiply Q’ by the distance the box extends “into” the figure, producing a dimension of length cubed over time, L3/T as in Equation Box 3-7.

\displaystyle Q_{total}=K\frac{H}{n_{d}}n_{f}w : \displaystyle \frac{\textup{L}^3}{\textup{T}} (Box 3-7)

where:

w = distance that the flow net domain extends in the direction normal to the plane of the diagram (L)

The formula can be used to calculate volumetric flow through graphically constructed flow nets with complex geometry. The formula for determining the volumetric flow through a flow net does not involve the absolute dimensions of the length and height of the system. It uses only relative values of the length and height of the box, so the drawing must be to scale. That is, the relative length and width of the drawing must be correct. Also, the distance that the system extends normal to the diagram must be known to determine the total flow through the system.

By substituting the appropriate values of nf, nd, H, K and w for the rectangular box into the equation for volumetric discharge through a flow net, the calculated flow equals that calculated by Darcy’s Law at the beginning of this box.

\displaystyle Q_{total}=\left (0.4\ \frac{\textup{cm}}{\textup{s}} \right )(6\ \textup{cm})\left (\frac{3}{6} \right )(50 \textup{cm}) = \displaystyle 60\ \frac{\textup{cm}^3}{\textup{s}}

Return to where text links to Box 3

Từ khóa » Volumetric Flow Formula