Các Bài Toán Về Véc Tơ Trong Không Gian

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ Các bài toán về véc tơ trong không gian Toán lớp 11, tài liệu bao gồm 0 trang, tuyển chọn Các bài toán về véc tơ trong không gian đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Các bài toán về véc tơ trong không gian gồm các nội dung chính sau:

A. Lý thuyết

- Tóm tắt lý thuyết ngắn gọn Các bài toán về véc tơ trong không gian.

B. Các dạng toán về véc tơ trong không gian

- Gồm 10 ví dụ minh họa đa dạng của Các bài toán về véc tơ trong không gian có đáp án và lời giải chi tiết.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

DẠNG 1. CÁC BÀI TOÁN VỀ VÉC TƠ TRONG KHÔNG GIAN

A. LÝ THUYẾT

Cho các véc tơ tùy ý a→,b→,c→ và k,l∈ℝ.

1. Cộngvéctơ:

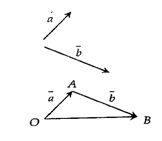
Lấy điểm O tùy ý trong không gian, vẽ OA→=a→,AB→=b→, thì OB→=a→+b→

Quy tắc ba điểm: Cho ba điểm M,N,K bất kỳ thì MN→=MK→+KN→

2. Trừ véc tơ: a→−b→=a→+(−b→)

Quy tắc ba điểm: MN→=KN→−KM→.

Quy tắc hình bình hành: Cho hình bình hành ABCD ta có: AC→=AB→+AD→.

Quy tắc hình hộp: Cho hình hộp ABCD.A'B'C'D' ta có AC'→=AB→+AD→+→.

3. Tích véc tơ:

Tích của véc tơ a→ với một số thực k là một véc tơ. Kí hiệu là k.a→

+) Cùng hướng với a→ nếu k>0.

+) Ngược hướng với a→ nếu k<0.

+) k.a→=k.a→.

Hệ quả: Nếu I là trung điểm của A,B,O tùy ý thì OA→+OB→=2OI→.

4. Tích vô hướng của hai véc tơ.

+) Định nghĩa: a→.b→=a→.b→.cosa→,b→.

+) Hệ quả: a→⊥b→⇔a→.b→=0.

+) a→2=a→.a→=a→2.

+) Với ba điểm A,B,C ta có AB.AC=AB2+AC2−BC22.

+) Quy tắc hình chiếu: Cho hai véc tơ a→,b→. Gọi a'→ là hình chiếu vuông góc của a'→ trên đường thẳng chứa b→ thì: a→.b→=a'→.b→.

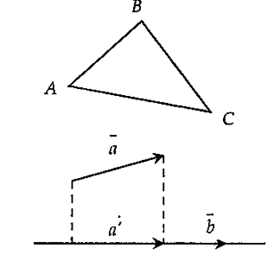
5. Định nghĩa: Ba véc tơ a→,b→,c→ gọi là đồng phẳng nếu giá của chúng cùng song song hoặc nằm trên một mặt phẳng.

6. Các định lý:

a) Cho a→,b→ không cùng phương: a→,b→,c→ đồng phẳng ⇔∃m,n∈ℝ:c→=ma→+nb→ ( với m,n xác định duy nhất).

b) Nếu ba véc tơ a→,b→,c→ không đồng phẳng thì mọi véc tơ đều được biểu diễn dưới dạng: x→=ma→+nb→+kc→ với m,n,k xác định duy nhất.

B. CÁC DẠNG TOÁN VỀ VÉC TƠ TRONG KHÔNG GIAN.

Ví dụ 1. Cho tứ diện đều ABCD, M là trung điểm của cạnh AB và G là trộng tâm cảu tam giác BCD. Đặt AB→=b→,AC→=c→,AD→=d→. Phân tích véc tơ MG→ theo d→,b→,c→ .

A. MG→=−16b→+13c→+13d→. B. MG→=16b→+13c→+13d→.

C. MG→=−16b→−13c→+13d→ . D. MG→=−16b→−13c→−13d→.

Xem thêm