Các Dạng Bài Tập Về định Lý Viet Lớp 9 Cơ Bản Và Nâng Cao - Icongchuc

Các dạng bài tập về định lý Viet lớp 9 cơ bản và nâng cao. Định lý Viet là một kiến thức quan trọng ở bậc THCS mà bạn cần phải nhớ khi muốn học tốt toán. Không chỉ có trong bài kiểm tra, thi học kì mà còn xuất hiện nhiều trong đề thi học sinh giỏi, thi vào 10. 

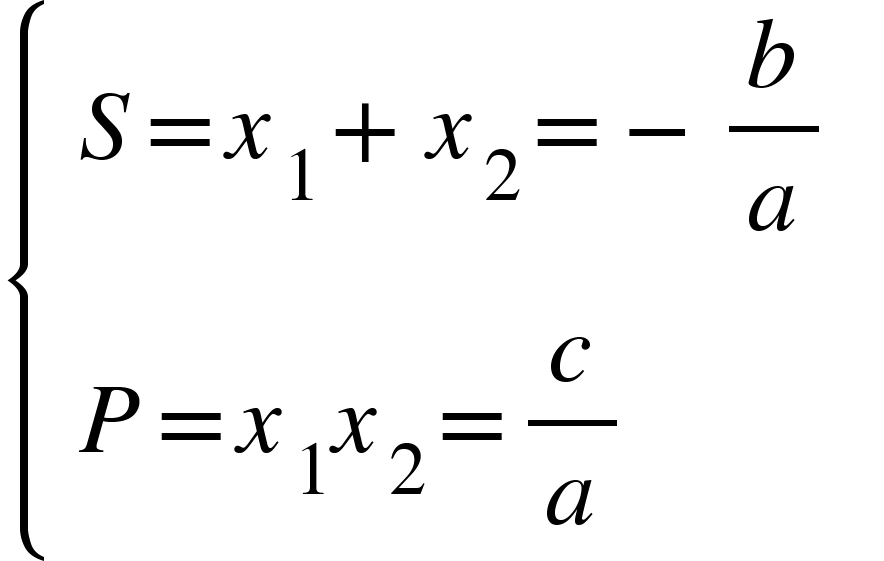
Nội dung chính:

Toggle

• Bài tập về định lý Viet lớp 9 – Bài tập vi et lớp 9
  • Dạng 1. Dựa định lý Viet để tính nhẩm nghiệm
  • Dạng 2. Tính giá trị của biểu thức giữa các nghiệm
  • Dạng 3. Tìm hai số khi biết tổng và tích
  • Dạng 4. Phân tích tam thức bâc hai thành nhân tử
  • Dạng 5. Tìm điều kiện của tham số để phương trình bậc 2 có một nghiệm x = x1 cho trước. Tìm nghiệm thứ hai
  • Dạng 6. Xác định tham số để các nghiệm của phương trình bậc 2 thỏa mãn hệ một điều kiện cho trước.
  • Dạng 7. Lập phương trình bậc trình bậc hai một ẩn khi biết hai nghiệm của nó hoặc hai nghiệm có liên quan tới hai nghiệm của một phương trình đã cho
  • Dạng 8. Tìm hệ thức liên hệ giữa hai nghiệm của phương trình bậc hai không phụ thuộc vào tham số
  • Dạng 9. Chứng minh hệ thức giữa các nghiệm của phương trình bậc 2 hoặc hai phương trình bậc 2
  • Dạng 10. xét dấu các nghiêm của phương trình bậc 2, so sánh nghiệm của phương trình bậc 2 với một số cho trước
  • Dạng 11. Nghiệm chung của hai hay nhiều phương trình, hai phương trình tương đương
  • Dạng 12. Ứng dụng của định lý vi-ét vào giải các bài toán số học
• Bài tập định lý viet lớp 9

Bài tập về định lý Viet lớp 9 – Bài tập vi et lớp 9

Dạng 1. Dựa định lý Viet để tính nhẩm nghiệm

Thường thì khi gặp bài toán giải phương trình bậc 2, nhiều bạn dùng ngay biệt thức Δ để suy ra các nghiệm x1, x2 (nếu có). Tuy nhiên dựa vào hệ thức Viet ta có một cách tính nhẩm nhanh hơn

Dạng 2. Tính giá trị của biểu thức giữa các nghiệm

Nếu \[a{x^2} + bx + c = 0\] ( với a ≠ 0) có hai nghiệm x1, x2 thì ta có thể biểu thị các biểu thức đối xứng giữa các nghiệm theo \[S = {x_1} + {x_2}\] và \[P = {x_1}.{x_2}\]       Chú ý: Khi tính giá trị của một biểu thức giữa các nghiệm thông thường ta biến đổi sao cho trong biểu thức đó xuất hiện tổng và tích các nghiệm rồi áp dụng định lý Vi-ét để giải.

Dạng 3. Tìm hai số khi biết tổng và tích

Dạng 4. Phân tích tam thức bâc hai thành nhân tử

Giả sử \[a{x^2} + bx + c = 0\] ( với a ≠ 0) có Δ ≥ 0 Ví dụ: Phân tích \[3{x^2} + 5x – 8\] thành nhân tử   Giải   Nhận xét: \[3{x^2} + 5x – 8 = 0\] có a + b + c = 3 + 5 – 8 = 0 => có 2 nghiệm là \[{x_1} = 1{\rm{ ; }}{x_2} = \frac{{ – 8}}{3}\] Khi này tam thức \[3{x^2} + 5x – 8 = \left( {x – 1} \right)\left( {3x + 8} \right)\]  

Dạng 5. Tìm điều kiện của tham số để phương trình bậc 2 có một nghiệm x = x1 cho trước. Tìm nghiệm thứ hai

Cách 1: Bước 1: Tìm điều kiện để phương trình có hai nghiệm Δ ≥ 0 (Δ ≥ 0 ) (*) Bước 2: Thay x = x1 vào phương trình đã cho tìm giá trị của tham số Bước 3: Đối chiếu giá trị vừa tìm được với điều kiện (*) để kết luận   Cách 2: Bước 1. Thay x = x1 vào phương trình đã cho tìm được giá trị của tham số. Bước 2. Thay giá trị tìm được của tham số vào phương trình và giải phương trình Nếu sau khi thay giá trị của tham số vào phương trình đã cho mà có Δ < 0 thì kết luận không có giá trị nào của tham số để phương trình có nghiệm x1 cho trước.   Để tìm nghiệm thứ hai ta có thể làm như sau   Cách 1: Thay giá trị của tham số tìm được vào phương trình rồi giải phương trình. Cách 2: Thay giá trị của tham số tìm được vào công thức tổng 2 nghiệm để tìm nghiệm thứ hai. Cách 3: Thay giá trị của tham số tìm được vào công thức tích hai nghiệm để tìm nghiệm thứ hai.   Ví dụ: Với giá trị nào của k thì:   a) Phương trình \[2{x^2} + kx – 10 = 0\] có một nghiệm x = 2. Tìm nghiệm kia   b) Phương trình \[\left( {k – 5} \right){x^2} – \left( {k – 2} \right)x + 2k = 0\] có một nghiệm x = – 2. Tìm nghiệm kia   c) Phương trình \[k{x^2} – kx – 72\] có một nghiệm x = – 3. Tìm nghiệm kia?   Lời giải  

Dạng 6. Xác định tham số để các nghiệm của phương trình bậc 2 thỏa mãn hệ một điều kiện cho trước.

  Chú ý: Sau khi tìm được tham số ta phải đối chiếu với điều kiện phương trình có nghiệm.   Ví dụ: Cho phương trình: \[{x^2} – 6x + m = 0\]. Tính giá trị của m biết phương trình có hai nghiệm x1, x2 thỏa mãn điều kiện: \[{x_1} – {x_2} = 4\]    

Dạng 7. Lập phương trình bậc trình bậc hai một ẩn khi biết hai nghiệm của nó hoặc hai nghiệm có liên quan tới hai nghiệm của một phương trình đã cho

Để lập phương trình bậc hai khi biết hai nghiệm là α và β ta cần phải tính α + β và α.β, áp dụng định lý vi-ét đảo ta có phương trình cần lập là: \[{x^2} – \left( {\alpha + \beta } \right)x + \alpha .\beta = 0\]   Ví dụ: Gọi x1, x2 là hai nghiệm của phương trình \[{x^2} – 7x + 3 = 0\].Hãy lập phương trình bậc hai có hai nghiệm là \[2{x_1} – {x_2}\] và \[2{x_2} – {x_1}\].   Giải:

Dạng 8. Tìm hệ thức liên hệ giữa hai nghiệm của phương trình bậc hai không phụ thuộc vào tham số

Ví dụ: Cho phương trình \[8{x^2} – 4\left( {m – 2} \right)x + m\left( {m – 4} \right) = 0\]. Định m để phương trình có hai nghiệm x1, x2. Tìm hệ thức giữa hai nghiệm độc lập với m, suy ra vị trí của các nghiệm với hai số – 1 và 1.   Lời giải   Phương trình đã cho là phương trình bậc 2 có

Dạng 9. Chứng minh hệ thức giữa các nghiệm của phương trình bậc 2 hoặc hai phương trình bậc 2

Dạng 10. xét dấu các nghiêm của phương trình bậc 2, so sánh nghiệm của phương trình bậc 2 với một số cho trước

  Ví dụ: Cho phương trình \[{x^2} – \left( {2m + 3} \right)x + {m^2} + 3m + 2 = 0\]. Tìm m để phương trình có hai nghiệm đối nhau   Lời giải

Dạng 11. Nghiệm chung của hai hay nhiều phương trình, hai phương trình tương đương

 

Dạng 12. Ứng dụng của định lý vi-ét vào giải các bài toán số học

Ví dụ: Tìm các số nguyên dương x, y thỏa mãn phương trình \[{x^3} + {y^3} + = 3xy\]   Lời giải  

Bài tập định lý viet lớp 9

Download [70.82 KB]

Xem thêm Phiếu bài tập phương trình bậc hai lớp 9 nâng cao