Các Dạng Bài Tập Về Tỉ Số Lượng Giác Của Góc Nhọn - Toán Lớp 9
Có thể bạn quan tâm
Bài viết này chúng ta cùng hệ thống lại một số công thức về tỉ số lượng giác của góc nhọn và đặc biệt vận dụng các công thức này để giải các bài tập liên quan để rèn kỹ năng giải toán vận dụng công thức.
1. Tỉ số lượng giác của góc nhọn
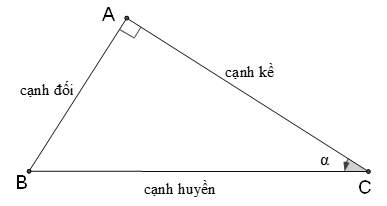 • sinα = cạnh đối/cạnh huyền
• sinα = cạnh đối/cạnh huyền 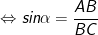
• cosα = cạnh kề/cạnh huyền 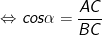
• tanα = cạnh đối/cạnh kề 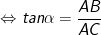
• cotα = cạnh kề/cạnh đối 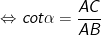
* Cách nhớ gợi ý: Sin = Đối/Huyền; Cos = Kề/Huyền; Tan = Đối/Kề; Cot - Kề/Đối nên cách nhớ như sau: Sin Đi Học, Cos Không Hư, Tan Đoàn Kết, Cot Kết Đoàn.
Ngoài ra khi giải các bài tập về tỉ số lượng giác của góc nhọn các em cũng sẽ vận dụng các công thức hệ thức lượng trong tam giác vuông.
2. Các dạng bài tập tỉ số lượng giác của góc nhọn
° Dạng 1: Tính các tỉ số lượng giác của góc
* Ví dụ 1 (Bài 15 trang 77 SGK Toán 9 Tập 1): Cho tam giác ABC vuông tại A. Biết cosB = 0,8, hãy tính các tỉ số lượng giác của góc C.
* Lời giải:
- Ta có: Góc B và góc C là 2 góc phụ nhau, tức là:
∠B + ∠C = 90o nên sinC = cosB = 0,8
- Từ công thức sin2C + cos2C = 1 ta suy ra:
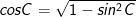 (do góc C nhọn nên sinC, cosC >0).
(do góc C nhọn nên sinC, cosC >0).
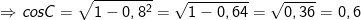
- Lại có: 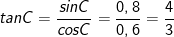
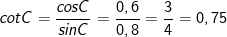
- Vật sinC = 0,8; cosC = 0,6; tanC = 4/3; cotC = 0,75.
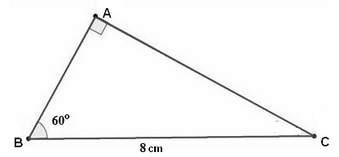
* Ví dụ 2 (Bài 16 trang 77 SGK Toán 9 Tập 1): Cho tam giác vuông có một góc 60o và cạnh huyền có độ dài là 8. Hãy tìm độ dài của cạnh đối diện với góc 60o.
 * Lời giải:
* Lời giải:
- Như minh họa hình trên, cạnh đối diện với góc 600 là AC, ta có:
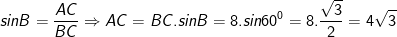
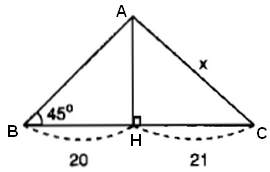
* Ví dụ (Bài 17 trang 77 SGK Toán 9 Tập 1): Tìm x trong hình:
 * Lời giải:
* Lời giải:
- Ta ký hiệu như hình trên.
- Vì ∠B = 45o nên ∠HAB = 90o - 45o = 45o (góc B, và góc HAB phụ nhau trong tam giác vuông ABH)
Suy ra tam giác ABH là tam giác vuông cân tại H, nên AH = HB = 20
- Áp dụng định lí Pitago trong tam giác vuông AHC có:
x2 = AH2 + HC2 = 202 + 212 = 841
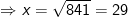
° Dạng 2: Chứng minh các đẳng thức
* Ví dụ 1: Chứng minh các đẳng thức sau:
a) cos4α - sin4α = cos2α - sin2α
b) sin4α + cos2α.sin2α + sin2α = 2sin2α
* Lời giải:
a) cos4α - sin4α = cos2α - sin2α
- Ta biến đổi vế phải của đẳng thức:
VP = cos4α - sin4α = (cos2α)2 - (sin2α)2
= (cos2α - sin2α)(sin2α + cos2α)
=(cos2α - sin2α).1 = cos2α - sin2α = VT
→ Vậy đẳng thức được chứng minh.
b) sin4α + cos2α.sin2α + sin2α = 2sin2α
- Ta có:
VP = sin4α + cos2α.sin2α + sin2α
= sin2α.(sin2α + cos2α + 1)
= sin2α.(1 + 1) = 2.sin2α = VT
→ Vậy đẳng thức được chứng minh.
* Ví dụ 2: Tam giác nhọn ABC có diện tích S, đường cao AH = h. Cho biết S = h2, Chứng minh rằng cotB + cotC = 2.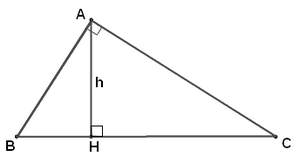 * Lời giải:
* Lời giải:
- Theo công thức tính diện tích tam giác thì: 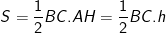
- Theo bài ra thì SABC = h2 nên ta có: 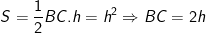
- Mà 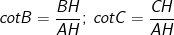
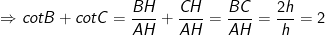
→ Vậy ta có điều phải chứng minh.
° Dạng 3: Tính giá trị của biểu thức
* Ví dụ : Tính giá trị của các biểu thức sau mà không dùng bảng số hoặc máy tính
a) A = sin2150 + sin2250 + sin2350 + sin2450 + sin2550 + sin2650 + sin2750
b) B = 4cos2α - 3sin2α với cosα = 4/7.
* Lời giải:
a) A = sin2150 + sin2250 + sin2350 + sin2450 + sin2550 + sin2650 + sin2750
=(sin2150 + sin2750) + (sin2250 + sin2650 ) + (sin2350 + sin2550) + sin2450
= (sin2150 + cos2150) + (sin2250 + cos2250 ) + (sin2350 + cos2350 ) + sin2450
= 1 + 1 + 1 + 1/2 = 7/2
b) B = 4cos2α - 3sin2α với cosα = 4/7
- Ta có: sin2α + cos2α = 1
⇔ sin2α = 1 - cos2α = 1 - (4/7)2 = 33/49
- Suy ra: B = 4cos2α - 3sin2α = 4.(16/49) - 3.(33/49) = -5/7.
° Dạng 4: Chứng minh biểu thức không phụ thuộc giá trị của góc nhọn
* Ví dụ: Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trị của các góc nhọn α, β
a) cos2α.cos2β + cos2α.sin2β + sin2 α
b) 2(sinα - cosα)2 - (sinα + cosα)2 + 6sinα.cosα
c) (tanα - cotα)2 - (tanα + cotα)2
* Lời giải:
a) cos2α.cos2β + cos2 α.sin2β + sin2α
= cos2α(cos2β + sin2β) + sin2α
= cos2α.1 + sin2α = 1
b) 2(sinα - cosα)2 - (sinα + cosα)2 + 6 sinα.cosα
= 2(sin2α + cos2α - 2sinα.cosα) - (sin2α + cos2α + 2sinα.cosα) + 6sinα.cosα
= 2(1 - 2sinα.cosα) - (1 + 2sinα.cosα) + 6sinα.cosα
= 1 - 6sinα.cosα + 6sinα.cosα = 1
c) (tanα - cotα)2 - (tanα + cotα)2
= (tan2α - 2.tanα.cotα + cot2α) - (tan2α + 2tanα.cotα + cot2α)
= -4 tanα.cotα = -4.1 = -4
+ Nếu không khai triển dạng hẳng đẳng thức dạng (A-B)2 và (A+B)2 như trên, các em có thể sử dụng dạng A2 - B2 = (A - B)(A + B), khi đó:
(tanα - cotα)2 - (tanα + cotα)2
= [(tanα - cotα) - (tanα + cotα)][(tanα - cotα) + (tanα + cotα)]
= (-2cotα).(2tanα) = -4.cotα.tanα = -4.1 = -4.
Từ khóa » Các Dạng Toán Lượng Giác 9
-
Bài Tập Tỉ Số Lượng Giác – Hình Học 9- đầy đủ Các Dạng Toán
-
Bài Tập Tỉ Số Lượng Giác Của Góc Nhọn Chọn Lọc, Có Lời Giải - Toán Lớp 9
-
Công Thức Lượng Giác Lớp 9 Hay Nhất - TopLoigiai
-
Cách Giải Bài Dạng: Tính Tỉ Số Lượng Giác Của Một Góc Nhọn Toán Lớp 9
-
50 Bài Tập Về Các Bài Toán Về Tỉ Số Lượng Giác Của Góc Nhọn (có đáp ...
-
Toán 9: Tỉ Số Lượng Giác Của Góc Nhọn- Lý Thuyết Và Bài Tập
-
Tổng Hợp Tất Tần Tất Công Thức Lượng Giác Lớp 9 Cần Nhớ
-
Toán 9 - Chuyên đề: Tỷ Số Lượng Giác - TaiLieu.VN
-
Các Dạng Bài Tập Lượng Giác Lớp 9 Hay Nhất, Toán 9
-
Sin Cos Tan Lớp 9 Và Các Dạng Bài Tập áp Dụng Chi Tiết - VIP VIỆT
-
[Top Bình Chọn] - Bài Tập Lượng Giác Lớp 9 - Trần Gia Hưng
-
Tỉ Số Lượng Giác Của Góc Nhọn Và Các Dạng Toán Thường Gặp
-
Chuyên đề Tỉ Số Lượng Giác Của Góc Nhọn, Hệ Thức Về Cạnh Và Góc ...
-
Bài Tập Tỉ Số Lượng Giác Của Góc Nhọn - Hình Học 9 Chương I