Cách Bấm Máy Tính đạo Hàm

Trang chủ » Cách Bấm Máy Tìm Hàm Số Liên Tục » Cách Bấm Máy Tính đạo Hàm

Có thể bạn quan tâm

Cách bấm máy tính đạo hàm Bấm máy tính đạo hàm Toán 11 Tải về Lớp: Lớp 11 Môn: Toán Loại File: Word + PDF Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Cách tính đạo hàm bằng máy tính Casio Toán 11

  • A. Cách bấm máy tính đạo hàm cấp 1
  • B. Cách bấm máy tính đạo hàm cấp 2
  • C. Tính đạo hàm của hàm số bằng máy tính cầm tay
  • D. Bài tập tính đạo hàm bằng máy tính casio

Bấm máy tính Casio tính đạo hàm Toán lớp 11 vừa được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi bài viết dưới đây nhé.

- Trong giải tích toán học, đạo hàm là một hàm mô tả sự biến thiên tại một điểm. Nói cách khác, đạo hàm là tỷ số giữa số gia và hàm số tại một điểm x0. Độ lớn của biến thể và hướng của biến thể đại diện cho giá trị của đạo hàm. Tuy nhiên, theo một định nghĩa khác của Wikipedia thì đạo hàm được hiểu là sự biến thiên lên xuống của hàm số tại điểm thay đổi. Ngoài ra trong Vật lý đạo hàm được coi là vận tốc tức thời khi một vật đang chuyển động.

A. Cách bấm máy tính đạo hàm cấp 1

Bấm máy tính cầm tay tính đạo hàm cấp 1

  • Bước 1: Bấm tổ hợp phím Cách bấm máy tính đạo hàm + Cách bấm máy tính đạo hàm
  • Bước 2: Nhập hàm số tại điểm x0 và ẩn bằng.

Ví dụ 1: Cho hàm số y = \sqrt {4x - 1}\(y = \sqrt {4x - 1}\). Tính đạo hàm của hàm số tại x = 2

Hướng dẫn giải

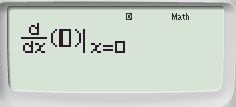
Bước 1: Bấm tổ hợp phím  Cách bấm máy tính đạo hàm+Cách bấm máy tính đạo hàm  ta được: Cách bấm máy tính đạo hàm

Bước 2: Nhập hàm số y = \sqrt {4x - 1}\(y = \sqrt {4x - 1}\) và x = 2 ta được 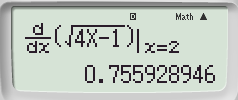Cách bấm máy tính đạo hàm

Nhấn “=” ta được kết quả cần tìm: 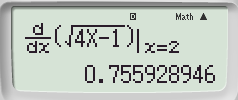Cách bấm máy tính đạo hàm

B. Cách bấm máy tính đạo hàm cấp 2

Công thức tính đạo hàm cấp 2:

Từ khóa » Cách Bấm Máy Tìm Hàm Số Liên Tục