Cách Bấm Máy Tính Lim - Giới Hạn Hàm Số
Có thể bạn quan tâm
Giới hạn của hàm số
- A. Giới hạn hàm lượng giác
- B. Giới hạn hàm siêu việt
- C. Cách tính lim bằng máy tính
- D. Tính lim bằng máy tính
Tính giới hạn Lim đưa ra phương pháp và các ví dụ cụ thể, giúp các bạn học sinh THPT ôn tập và củng cố kiến thức về dạng toán tính giới hạn 11 và lớp 12. Tài liệu bao gồmcách bấm máy tính giới hạn các bài tập ví dụ minh họa có lời giải và bài tập rèn luyện giúp các bạn bao quát nhiều dạng bài chuyên đề giới hạn hàm số. Chúc các bạn học tập hiệu quả!
A. Giới hạn hàm lượng giác
B. Giới hạn hàm siêu việt
C. Cách tính lim bằng máy tính
Bước 1: Nhập hàm số
Bước 2: Sử dụng hàm CALC để tính giới hạn
Quy ước tính giới hạn vô định như sau:

Chú ý: Vì đây là thủ thuật để tính giới hạn nên kết quả máy tính đưa ra chỉ sấp xỉ đáp án, nên ta sẽ chọn đáp án gần nhất.
D. Tính lim bằng máy tính
Ví dụ 1: Tính giới hạn của hàm số  khi x tiến tới 0.
khi x tiến tới 0.
A. 1 | B. 8 | C. 2 | D. 4 |
Hướng dẫn giải
Quan sát hàm số ta có ![]()
Sử dụng máy tính Casio để tính giới hạn như sau:
Bước 1: Nhập hàm số vào máy tính ta được:

Bước 2: Nhấn phím CALC ➟ 0 + 10^(-6) ➟ Nhấn dấu “=” ta được
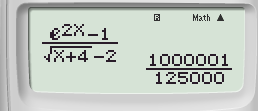
Bước 3: Nhấn phím ![]() ta được kết quả:
ta được kết quả:
Kết quả gần nhất là 8
Vậy chọn đáp án B
Ví dụ 2: Tính ![]()
A. | B. 1 | C. | D. |
Hướng dẫn giải
Quan sát hàm số ta thấy đề bài không đề cập đến giá trị n tiến tới bao nhiêu thì ta sẽ hiểu rằng ![]()
Sử dụng máy tính Casio để tính giới hạn như sau:
Bước 1: Nhập hàm số vào máy tính ta được:
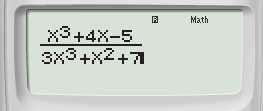
Bước 2: Nhấn phím CALC ➟ 10^(9) ➟ Nhấn dấu “=” ta được
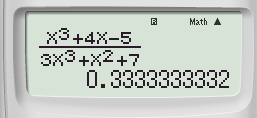
Kết quả gần nhất là ![]()
Vậy chọn đáp án A
Ví dụ 3: Giới hạn ![]() bằng bao nhiêu?
bằng bao nhiêu?
A. | B. | C. 0 | D. -1 |
Hướng dẫn giải
Quan sát hàm số ta thấy đề bài không đề cập đến giá trị n tiến tới bao nhiêu thì ta sẽ hiểu rằng ![]()
Tuy nhiên chú ý, bài này liên quan đ ến hàm lũy thừa (số mũ) mà máy tính chỉ tính được số mũ tối đa là 100 nên ta chọn x = 100
Sử dụng máy tính Casio để tính giới hạn như sau:
Bước 1: Nhập hàm số vào máy tính ta được:
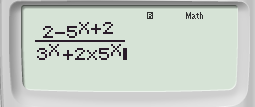
Bước 2: Nhấn phím CALC ➟ 100 ➟ Nhấn dấu “=” ta được
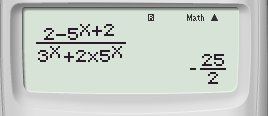
Vậy chọn đáp án A
Ví dụ 4: Tính giới hạn ![]()
A. 3 | B. 1 | C. 0 | D. 2 |
Hướng dẫn giải
Đối với dãy số như thế này chúng ta không thể nhập vào máy tính cả biểu thức được
Bước 1: Tiến hành rút gọn biểu thức như sau:

Sau khi rút gọn ra thực hiện bấm máy tính tương tự những ví dụ trên.
Quan sát hàm số ta thấy đề bài không đề cập đến giá trị n tiến tới bao nhiêu thì ta sẽ hiểu rằng ![]()
Sử dụng máy tính Casio để tính giới hạn như sau:
Bước 2: Nhập hàm số vào máy tính ta được:
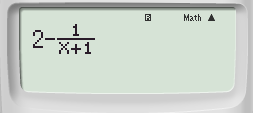
Bước 3: Nhấn phím CALC ➟ 1➟ Nhấn dấu “=” ta được
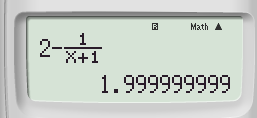
Kết quả nhận được gần 2 nhất
Chọn đáp án D
-----------------------------------------------------------
Hi vọng Chuyên đề Giới hạn của hàm số là tài liệu hữu ích cho các bạn ôn tập kiểm tra năng lực, bổ trợ cho quá trình học tập trong chương trình THPT cũng như ôn luyện cho kì thi THPT Quốc gia. Chúc các bạn học tốt!
Từ khóa » Tính Lim
-
Công Thức Tính Lim - Gia Sư Tâm Tài Đức
-
Cách Tính Lim Bằng Tay Của Hàm Số, Bằng Phương Pháp Thủ Công ...
-
7 Cách Tính Lim Cực Kỳ đơn Giản Và Chính Xác 100% [VD Minh Họa]
-
Cách Bấm Máy Tính Lim, Tích Phân, đạo Hàm, Nguyên Hàm Thi Trắc ...
-
Giới Hạn Hàm Số Lớp 11: Lý Thuyết, Công Thức, Bài Tập - Boxthuthuat
-
Toán 11 - Giới Hạn Của Hàm Số, Cách Tính Và Bài Tập áp Dụng
-
Giới Hạn Dãy Số Tính Lim - Toán 11 - Thầy Nguyễn Quốc Chí
-
Giải Tích Các Ví Dụ - Mathway
-
Tính Giới Hạn Của Hàm Số Khi X Dần Tới Vô Cực
-
Máy Tính Giới Hạn Với Các Bước - Trực Tuyến & Miễn Phí!
-
Hướng Dẫn Cách Bấm Máy Tính Lim Mới Nhất - ReviewEdu
-
Tính Giới Hạn Hàm đa Thức, Hàm Phân Thức Và Giới Hạn Một Bên
-
Cách Tính Lim, Thủ Thuật Tính Giới Hạn Dãy Số Nhanh Nhất
-
Công Thức Tính Lim - TBDN