Cách Chứng Minh Các điểm (4 điểm) Cùng Thuộc Một đường Tròn

• Trang chủ
• Tin tức mới
• Kiến thức THCS
• Trung học CS lớp 9
• Môn Toán 9
• Cách chứng minh các điểm (4 điểm) cùng thuộc một đường tròn - Toán 9 chuyên đề

Cách chứng minh các điểm (4 điểm) cùng thuộc một đường tròn - Toán 9 chuyên đề 16:49:4716/05/2022

Chứng minh các điểm cùng nằm trên một đường tròn là một dạng bài tập hình học phổ biến và quan trọng trong chương trình Toán 9. Để giải quyết dạng toán này, bạn cần nắm vững các phương pháp cơ bản và linh hoạt áp dụng vào từng trường hợp cụ thể.

Phương pháp chứng minh 4 điểm thuộc một đường tròn

Có hai phương pháp chính để chứng minh nhiều điểm cùng thuộc một đường tròn:

1. Sử dụng định nghĩa: Chứng minh rằng các điểm đó cùng cách đều một điểm O cố định. Điểm O này chính là tâm của đường tròn.

2. Sử dụng tính chất của tứ giác nội tiếp: Chứng minh rằng một tứ giác có các đỉnh là 4 điểm cần chứng minh là một tứ giác nội tiếp. Một số dấu hiệu nhận biết tứ giác nội tiếp phổ biến là:

   • Tứ giác có tổng hai góc đối bằng 180o.

   • Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh dưới một góc bằng nhau.

   • Tứ giác có bốn đỉnh cùng cách đều một điểm.

 

Mở rộng: Chẳng hạn để chứng minh 5 điểm A, B, C, D, E cùng thuộc một đường tròn ta chứng minh 4 điểm ABCD và 4 điểm ABCE là các tứ giác nội tiếp cùng một đường tròn tâm O.

Dưới đây là một số ví dụ minh họa chi tiết.

Ví dụ 1: Cho tam giác ABC vuông tại A, đường cao AH. Từ M là điểm bất kì trên cạnh BC kẻ MD ⊥ AB, ME ⊥ AC. Chứng minh 5 điểm A, D, M, H, E cùng nằm trên một đường tròn.

Lời giải:

- Theo bài ra, có có hình sau: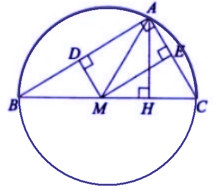

Xét tam giác vuông ADM có cạnh huyền AM

Xét tam giác vuông AEM có cạnh huyền AM

Và tam giác vuông AHM có cạnh huyền AM

Các tam giác này đều có chung cạnh huyền AM nên 3 đỉnh góc vuông nằm trên đường tròn đường kính AM có tâm là trung điểm của AM.

Vậy 5 điểm A, D, M, H, E cùng nằm trên một đường tròn.

Ví dụ 2: Cho tam giác ABC vuông tại A gọi D là điểm đối xứng với A qua cạnh BC. Chứng minh 4 điểm A, B, C, D cùng thuộc một đường tròn.

Lời giải:

- Ta có hình vẽ như sau:

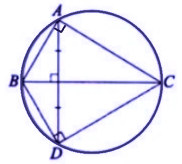
Vì D đối xứng với  A qua BC, B đối xứng với B qua BC, C đối xứng với C qua BC nên 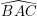 đối xứng với góc  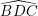qua BC.

Suy ra ∠BDC = ∠BAC = 900

Xét tam giác vuông BAC và BDC có chung cạnh huyền BC nên hai đỉnh góc vuông A, D nằm trên đường tròn đường kính BC, có tâm là trung điểm của cạnh huyền BC.

Vậy 4 điểm A, B, C, D cùng nằm trên một đường tròn.

Ví dụ 3: Cho tam giác ABC vuông tại A. Trên AC lấy điểm D. Hình chiếu của D lên BC là E, điểm đối xứng của E qua BD là F. Chứng minh 5 điểm A, B, E, D, F cùng nằm trên một đường tròn. Xác định tâm O của đường tròn đó.

Lời giải:

- Ta có hình vẽ như sau:

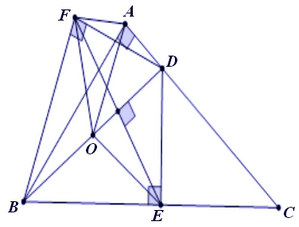- Theo giả thuyết, DE ⊥ BC nên ∠BEB = 900

- Vì E và F đối xứng với nhau qua BD nên BD là đường trung trực của đoạn thẳng EF nên suy ra:

 BF = BE và DF = DE

Suy ra: ΔBFD = ΔBED (c-c-c)

Suy ra: ∠BFD = ∠BEB = 900

- Gọi O là trung điểm của BD.

- Xét tam giác vuông ABD vuông tại A có AO là trung tuyến nên:

 AO = ½BD = OB = OD   (1)

- Xét tam giác vuông BDE vuông tại E có OE là trung tuyến nên:

 EO = ½BD = OB = OD   (2)

- Xét tam giác vuông BFD vuông tại F có OF là trung tuyến nên:

 FO = ½BD = OB = OD   (3)

Từ (1), (2) và (3) suy ra: OA = OB = OD = OE = OF.

Vậy 5 điểm A, B, E, D, F cùng nằm trên một đường tròn tâm O với O là trung điểm của BC.

Ví dụ 4: Cho hình thang cân ABCD (với AD//BC) có AB = 12cm, AC = 16cm, BC = 20 cm. Chứng minh 4 điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

Lời giải:

- Ta có hình minh họa như sau:

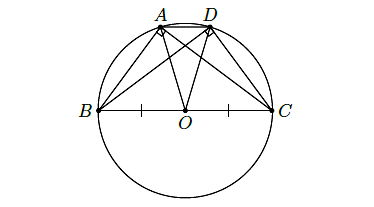Vì ABCD là hình thang cân với 2 đáy AD, BC nên AB = CD = 12 cm và BD = AC = 16 cm

Gọi O là trung điểm của BC,

Xét ΔABC có:

AB2 + AC2 = 122 + 162 = 202 = BC2

Vậy ΔABC vuông tại A. Vì vậy 3 đỉnh của tam giác ABC cùng thuộc đường tròn tâm O.

Tượng tự, ta cũng có ΔBCD vuông tại D. Vì vậy 3 đỉnh của tam giác BCD cùng thuộc đường tròn tâm O.

Vậy 4 điểm A, B, C, D cùng thuộc đường tròn (O) bán kính R = BC/2 = 20/2 = 10 (cm).

Ví dụ 5: Cho tứ giác ABCD có 

a) Chứng minh 4 điểm A, B, C, D cùng thuộc một đường tròn

b) Nếu AC = BD thì tứ giác ABCD là hình gì?

Lời giải:

Ta có hình minh họa như sau:

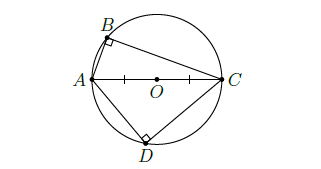
a) Gọi O là trung điểm của AC

Vì tam giác ABC vuông tại B nên ba đỉnh A, B, C cùng thuộc đường tròn (O)

Vì tam giác ACD vuông tại D nên ba đỉnh A, C, D cùng thuộc đường tròn (O)

Vậy 4 điểm A, B, C, D cùng thuộc đường tròn (O) đường kính AC

b) Nếu BD = AC thì BD là đường kính của (O)

Suy ra 

Vậy tứ giác ABCD có  

Nên ABCD là hình chữ nhật.

Các phương pháp chứng minh 4 điểm cùng thuộc một đường tròn đều dựa trên việc tìm ra một điểm cố định (tâm đường tròn) cách đều 4 điểm đó, hoặc chứng minh 4 điểm đó tạo thành một tứ giác nội tiếp. Việc nắm vững các dấu hiệu này sẽ giúp bạn giải quyết các bài toán hình học một cách tự tin và chính xác.

Tweet

Đánh giá & nhận xét

Gửi an hay Trả lời - 22/12/2023 - 20:38 Gửi charm cho em hỏi vd3 có chứng minh được B,E,D,F thuộc đường tròn bk là trung điểm BD, tam giác ABD thuộc đtron bk là trung điểm BD không ạ em cảm ơn Trả lời - 05/03/2023 - 16:03 sybau dc nhe 09/11/2025 - 23:02 Gửi duonghongnhung hello Trả lời - 25/11/2022 - 19:36 Gửi Xem thêm bình luận 3 trong số 3 Tin liên quan

• Bài 4.27 trang 81 Toán 9 tập 1 Kết nối tri thức
• Bài 4.26 trang 81 Toán 9 tập 1 Kết nối tri thức
• Bài 4.25 trang 81 Toán 9 tập 1 Kết nối tri thức
• Bài 4.24 trang 81 Toán 9 tập 1 Kết nối tri thức
• Bài 4.23 trang 81 Toán 9 tập 1 Kết nối tri thức
• Bài 4.22 trang 81 Toán 9 tập 1 Kết nối tri thức
• Bài 4.21 trang 81 Toán 9 tập 1 Kết nối tri thức
• Bài 18 trang 58 Toán 9 tập 1 Chân trời sáng tạo
• Bài 17 trang 58 Toán 9 tập 1 Chân trời sáng tạo
• Bài 16 trang 58 Toán 9 tập 1 Chân trời sáng tạo
• Bài 15 trang 58 Toán 9 tập 1 Chân trời sáng tạo
• Bài 14 trang 58 Toán 9 tập 1 Chân trời sáng tạo
• Bài 13 trang 58 Toán 9 tập 1 Chân trời sáng tạo
• Bài 12 trang 58 Toán 9 tập 1 Chân trời sáng tạo
• Bài 11 trang 58 Toán 9 tập 1 Chân trời sáng tạo
• Bài 10 trang 57 Toán 9 tập 1 Chân trời sáng tạo
• Bài 9 trang 57 Toán 9 tập 1 Chân trời sáng tạo
• Bài 8 trang 57 Toán 9 tập 1 Chân trời sáng tạo
• Bài 7 trang 57 Toán 9 tập 1 Chân trời sáng tạo
• Bài 6 trang 57 Toán 9 tập 1 Chân trời sáng tạo
• Bài 5 trang 57 Toán 9 tập 1 Chân trời sáng tạo
• Bài 4 trang 57 Toán 9 tập 1 Chân trời sáng tạo
• Bài 3 trang 57 Toán 9 tập 1 Chân trời sáng tạo
• Bài 2 trang 57 Toán 9 tập 1 Chân trời sáng tạo
• Bài 1 trang 57 Toán 9 tập 1 Chân trời sáng tạo
• Bài 8 trang 56 Toán 9 tập 1 Chân trời sáng tạo
• Bài 7 trang 56 Toán 9 tập 1 Chân trời sáng tạo
• Bài 6 trang 56 Toán 9 tập 1 Chân trời sáng tạo
• Bài 5 trang 56 Toán 9 tập 1 Chân trời sáng tạo
• Bài 4 trang 56 Toán 9 tập 1 Chân trời sáng tạo
• Bài 3 trang 56 Toán 9 tập 1 Chân trời sáng tạo
• Bài 2 trang 56 Toán 9 tập 1 Chân trời sáng tạo
• Bài 1 trang 56 Toán 9 tập 1 Chân trời sáng tạo
• Bài 6 trang 10 Toán 9 tập 2 Chân trời sáng tạo
• Bài 5 trang 10 Toán 9 tập 2 Chân trời sáng tạo
• Bài 4 trang 10 Toán 9 tập 2 Chân trời sáng tạo
• Bài 3 trang 10 Toán 9 tập 2 Chân trời sáng tạo
• Bài 2 trang 10 Toán 9 tập 2 Chân trời sáng tạo
• Bài 1 trang 10 Toán 9 tập 2 Chân trời sáng tạo

Xem thêm

» Giải Toán 6 SGK Cánh Diều tập 2 » Giải Toán 6 SGK Chân trời tập 2 » Giải Toán 6 SGK Kết nối tập 2

» Giải Toán 7 SGK Cánh Diều tập 2 » Giải Toán 7 SGK Chân trời tập 2 » Giải Toán 7 SGK Kết nối tập 2

» Giải Toán 8 SGK Cánh Diều tập 2 » Giải Toán 8 SGK Chân trời tập 2 » Giải Toán 8 SGK Kết nối tập 2

» Giải Toán 10 SGK Cánh Diều tập 2 » Giải Toán 10 SGK Chân trời tập 2 » Giải Toán 10 SGK Kết nối tập 2

» Giải Toán 11 SGK Cánh Diều tập 2 » Giải Toán 11 SGK Chân trời tập 2 » Giải Toán 11 SGK Kết nối tập 2

» Giải Bài tập Vật Lí 10 SGK Chân trời sáng tạo » Lý thuyết Vật Lí 10 SGK Chân trời sáng tạo

» Giải Bài tập Hóa học 10 SGK Chân trời sáng tạo » Lý thuyết Hóa học 10 SGK Chân trời sáng tạo

Facebook

Tin mới Bài 18 trang 58 Toán 9 tập 1 Chân trời sáng tạo Bài 17 trang 58 Toán 9 tập 1 Chân trời sáng tạo Bài 16 trang 58 Toán 9 tập 1 Chân trời sáng tạo Bài 15 trang 58 Toán 9 tập 1 Chân trời sáng tạo Bài 14 trang 58 Toán 9 tập 1 Chân trời sáng tạo Tin cùng chuyên mục Giải bài 7 trang 46 SGK Toán 9 tập 1 Giải bài 6 trang 45 SGK Toán 9 tập 1 Giải bài 5 trang 45 SGK Toán 9 tập 1 Giải bài 4 trang 45 SGK Toán 9 tập 1 Giải bài 3 trang 45 SGK Toán 9 tập 1 Tin xem nhiều nhất Các dạng toán về phương trình đường thẳng trong mặt phẳng, bài tập vận dụng - Toán lớp 10 Cách tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của biểu thức - Toán lớp 9 Toán 11 - Giới hạn của hàm số, cách tính và bài tập áp dụng Chuyển động tròn đều, Công thức tính Tốc độ góc, Tốc độ dài và Gia tốc hướng tâm - Vật lý 10 bài 5 Các dạng toán về phương trình đường thẳng trong không gian oxyz và bài tập - Toán lớp 12 Tuyển sinh Phổ điểm khối D07 (D7) 2025 thi tốt nghiệp THPT Ngày 15/7 Bộ Giáo dục và Đào tạo công bố phổ điểm... Phổ điểm khối C03 (C3) 2025 thi tốt nghiệp THPT Phổ điểm khối C01 (C1) 2025 thi tốt nghiệp THPT Xem thêm Kiến thức THPT Bài 7.15 trang 43 Toán 11 tập 2 Kết nối tri thức Bài tập 7.15, trang 43 SGK Toán 11 Tập 2 (Kết nối tri... Bài 7.14 trang 43 Toán 11 tập 2 Kết nối tri thức Bài 7.13 trang 43 Toán 11 tập 2 Kết nối tri thức Xem thêm Kiến thức THCS Bài 7.2 trang 24 Toán 7 Tập 2 Kết nối tri thức Bài tập 7.2, trang 24 SGK Toán 7 Tập 2 (Kết nối tri... Bài 7.1 trang 24 Toán 7 Tập 2 Kết nối tri thức Bài 7.17 trang 33 Toán 7 Tập 2 Kết nối tri thức Xem thêm Trắc nghiệm online Toán 6 - Luỹ thừa Toán 7 - số hữu tỉ Toán THPT QG 2017 Xem thêm Tin học Cách so sánh 2 file Word nhanh bằng lệnh Compare để tìm sự khác biệt giữa 2 văn bản Nếu đã làm việc với máy tính, có lẽ việc soạn... Cách sử dụng hàm index và match - how to use index and match in... Cách sử dụng hàm IF nhiều điều kiện - How to use IF function... Xem thêm Ngoại ngữ Cách dùng say và tell trong câu gián tiếp, Sự khác nhau giữa tell và say trong câu gián tiếp Trong tiếng Anh, việc sử dụng đúng các động từ thể... Cách dùng thì hiện tại đơn, công thức và bài tập áp... Cách dùng thì hiện tại tiếp diễn, công thức và bài tập... Xem thêm Hướng nghiệp Trí Tuệ Nhân Tạo (AI) – Ngành Học Triển Vọng Trong Kỷ Nguyên Số AI (Artificial Intelligence) là ngành khoa học phát triển... Ngành Công Nghệ Thông Tin – Học Gì? Làm Gì? Cơ Hội Nghề... Ưu và nhược điểm của 5 ngành học Hot hiện nay Xem thêm Góc chia sẻ - giải trí 16 Best Places to visit in Ho Chi Minh City in 3 days Ho Chi Minh City is one of the most dynamic spots in Vietnam. There... Mục lục Ngữ Văn 11 Cánh Diều Tập 2 SGK Mục lục Ngữ Văn 11 Cánh Diều Tập 1 SGK Xem thêm Video Xem thêm