Cách Giải Hệ Phương Trình Có Chứa Tham Số M - Toán 9 Chuyên đề
Có thể bạn quan tâm
Bài tập hệ phương trình chứa tham số m thường có một số dạng như: Giải và biện luận số nghiệm của hệ phương trình theo tham số m (biện luận số nghiệm của hệ phương trình theo tham số m); Tìm m để hệ phương trình có nghiệm duy nhất; Tìm mối liên hệ giữa x và y không phụ thuộc vào m,...
» Đừng bỏ lỡ: Hai cách giải hệ phương trình bậc nhất 2 ẩn cực dễ hiểu
• Dạng 1: Giải hệ phương trình theo tham số m cho trước
* Phương pháp giải:
+ Bước 1: Thay giá trị của m vào hệ phương trình đã cho.
+ Bước 2: Giải hệ phương trình vừa nhận được theo các phương pháp đã biết.
+ Bước 3: Kết luận nghiệm của hệ phương trình
* Ví dụ 1: Cho hệ phương trình: 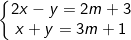
Giải hệ phương trình với m = 1.
* Lời giải:
- Với m = 1 ta có hệ: 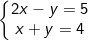
Cộng vế với vế pt(1) và pt(2) của hệ, ta được:
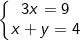
3x = 9 ⇔ x = 3 ⇒ y = 4 - 3 = 1.
Vậy với m = 1 hệ phương trình có nghiệm (x;y) = (3;1).
* Ví dụ 2: Cho hệ phương trình: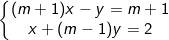
Giải hệ phương trình trên với m = 2.
* Lời giải:
- Khi m = 2 hệ phương trình có dạng: 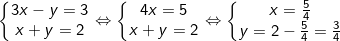
Vậy với m = 2 hệ phương trình có nghiệm 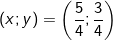

• Dạng 2: Giải và biện luận hệ phương trình theo tham số m (biện luận số nghiệm của hệ phương trình theo tham số).
* Phương pháp giải:
+ Bước 1: Đựa hệ phương trình về phương trình dạng bậc nhất dạng ax + b = 0. (sử dụng phương pháp thế, phương pháp cộng đại số,...)
+ Bước 2: Xét phương trình bậc nhất: ax + b = 0, (với a, b là hằng số) (*).
- TH1: Nếu a ≠ 0 thì phương trình (*) có nghiệm duy nhất x = -b/a. từ đó tìm được y.
- TH2: Nếu a = 0, b ≠ 0 thì phương trình (*) vô nghiệm.
- TH3: Nếu a = 0, b = 0 thì phương trình (*) có vô số nghiệm.
+ Bước 3: Kết luận nghiệm của hệ phương trình.
* Ví dụ: Cho hệ phương trình: 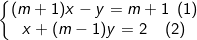
Giải và biện luận hệ phương trình bậc nhất hai ẩn trên theo tham số m.
* Lời giải:
- Từ PT (1) của hệ ta có: y = (m + 1)x - (m + 1); (3)
thế vào PT 2) ta được:
x + (m - 1)[(m + 1)x - (m + 1)] = 2
⇔ x + (m2 - 1)x - (m2 - 1) = 2
⇔ m2x = m2 + 1. (4).
- TH1: Nếu m ≠ 0 thì PT (4) có nghiệm duy nhất: 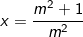 thay vào (3) ta có:
thay vào (3) ta có:
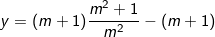
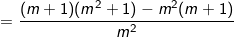
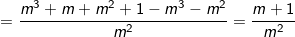
⇒ Hệ phương trình có nghiệm duy nhất 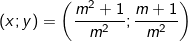
- TH2: Nếu m = 0 thì PT (4) trở thành 0x = 1 nên vô nghiệm.
⇒ Hệ phương trình đã cho vô nghiệm.
- Kết luận:
Với m ≠ 0 hệ phương trình có nghiệm duy nhất 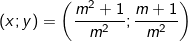 .
.
Với m = 0 hệ phương trình đã cho vô nghiệm.
• Dạng 3: Tìm m để hệ phương trình có nghiệm (x;y) thỏa điều kiện cho trước.
* Phương pháp giải:
+ Bước 1: Giải hệ phương trình tìm nghiệm(x; y) theo tham số m;
+ Bước 2: Thế nghiệm (x; y) vào biểu thức điều kiện cho trước rồi giải tìm m;
+ Bước 3: Kết luận giá trị m.
* Ví dụ 1: Cho hệ phương trình: 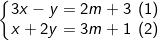
Tìm m để hệ phương trình có nghiệm (x;y) thỏa mãn x2 + y2 = 5.
* Lời giải:
- Nhân PT (1) với 2 và PT (2) với 1, ta được:
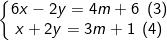
Cộng vế với vế của PT (3) và PT (4), ta được:
7x = 7m + 7 ⇔ x = m + 1
⇒ 2y = 3m + 1 - x = 3m + 1 - (m + 1) = 2m.
⇒ y = m.
Thế x = m + 1 và y = m vào điều kiện yêu cầu được: (m + 1)2 + (m)2 = 5
⇔ m2 + 2m + 1 + m2 = 5 ⇔ 2m2 + 2m - 4 = 0
⇔ m2 + m - 2 = 0 ⇔ m = 1 hoặc m = -2 (nhẩm theo Vi-ét, thấy phương trình bậc 2 theo m có a - b + c = 0).
- Kết luận: Vậy với m = 1 hoặc m = - 2 thì phương trình có nghiệm (x;y) thỏa mãn x2 + y2 = 5.
Khi đó có thể thấy cặp nghiệm tương ứng của hệ là (x;y) = (2;1) hoặc (x;y) = (-1;-2)
* Ví dụ 2: Cho hệ phương trình: 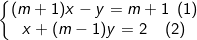
Tìm m để nghiệm của hệ phương trình thỏa mã (x + y) đạt giá trị nhỏ nhất:
* Lời giải:
- Theo lời giải của phần ví dụ ở dạng 2 ta đã giải hệ trên có nghiệm duy nhất khi m ≠ 0 là: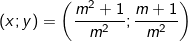
Ta có: 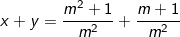
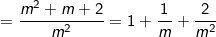
Đặt 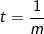 ta được:
ta được:
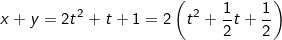
![\small =2\left [ \left (t+\frac{1}{4} \right )^2+\frac{7}{16} \right ]=2 \left ( t+\frac{1}{4} \right )^2+\frac{7}{8}\geq \frac{7}{8}](https://hayhochoi.vn/uploads/news/wyswyg/2021_07/1626224811fm36xazpkr.gif)
- Dấu "=" xảy ra khi và chỉ khi:
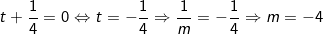
- Kết luận: Vậy với m = -4 thì hệ phương trình đã cho có nghiệm thỏa mãn x + y đạt GTNN bằng 7/8.
• Dạng 4: Tìm mối liên hệ giữa x và y không phụ thuộc vào tham số m.
* Phương pháp giải:
+ Bước 1: Giải hệ phương trình tìm nghiệm (x, y) theo tham số m;
+ Bước 2: Dùng phương pháp cộng đại số hoặc phương pháp thế làm mất tham số m;
+ Bước 3: Kết luận.
* Ví dụ: Cho hệ phương trình: 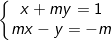
a) Chứng minh hệ luôn có nghiệm duy nhất (x;y) với mọi giá trị của m.
b) Tìm hệ thức liên hệ giữa x và y không phụ thuộc vào giá trị của m.
* Lời giải:
a) Ta có: 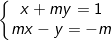
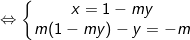
Từ PT: m(1-my) - y = - m
⇔ m -m2y - y = -m ⇔ 2m = y(m2 + 1)
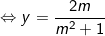
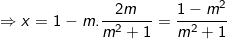
Vậy hệ phương trình luôn có nghiệm duy nhất: 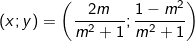
b) Ta thấy:
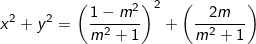
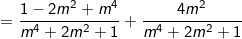
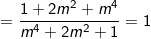
- Kết luận: Vậy x2 + y2 = 1 không phụ thuộc vào giá trị của m.
• Bài tập về hệ phương trình chứa tham số (tự giải)
* Bài tập 1: Cho hệ phương trình (a là tham số): 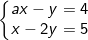
a) Giải hệ phương trình với a = 2.
b) Tìm a để hệ phương trình có nghiệm duy nhất thỏa x.y<0
c) Tìm a để hệ phương trình có nghiệp duy nhất thỏa x =|y|.
* Bài tập 2: Cho hệ phương trình (m là tham số):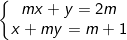
a) Giải hệ phương trình khi m = 3
b) Tìm m để hệ có nghiệm duy nhất (x;y) thỏa mãn x≥2 và y≥1.
* Bài tập 3: Cho hệ phương trình (a là tham số): 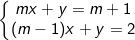
a) Giải hệ phương trình khi a = 2.
b) Chứng minh rằng với mọi giá trị của a thì hệ PT luôn có nghiệm duy nhất (x;y) thỏa mãn: 2x + y ≤ 3.
Từ khóa » Hệ Phương Trình Bậc Nhất Hai ẩn Chứa Tham Số
-
Cách Giải Hệ Phương Trình Bậc Nhất Hai ẩn Chứa Tham Số Cực Hay
-
Chuyên đề: Hệ Phương Trình Bậc Nhất Có Chứa Tham Số - Toán Cấp 2
-
Giải Và Biện Luận Hệ Hai Phương Trình Bậc Nhất Hai ẩn Có Chứa Tham ...
-
Hệ Phương Trình Bậc Nhất Chứa Tham Số - Abcdonline
-
108 Bài Toán Giải Và Biện Luận Hệ Phương Trình Bậc Nhất Chứa Tham Số
-
Chuyên đề Hệ Phương Trình Bậc Nhất Hai ẩn Số - Trường Quốc Học
-
Lý Thuyết Hệ Phương Trình Bậc Nhất Hai ẩn Chứa Tham Số Toán 9
-
Cách Giải Hệ Phương Trình Bậc Nhất Hai ẩn Chứa Tham Số Cực Hay
-
[Toán 9] Hệ Phương Trình Bậc Nhất 2 ẩn Chứa Tham Số | Thầy Đăng Hải
-
Hệ Hai Phương Trình Bậc Nhất Hai ẩn Chứa Tham Số - Toán 9 - YouTube
-
Biện Luận Hệ Phương Trình Bậc Nhất Chứa Tham Số - Học Toán 123
-
ĐS-Chuyên đề 15. HỆ PHƯƠNG TRÌNH CHỨA THAM SỐ.html
-
Lý Thuyết Hệ Hai Phương Trình Bậc Nhất Hai ẩn. | SGK Toán Lớp 9
-
Hệ Phương Trình Bậc Nhất Hai ẩn Chứa Tham Số-Toán 9 Có Lời Giải Chi ...