Cách Giải Phương Trình Bậc 3 Nhanh Chóng - Gia Sư Trí Tuệ Việt

Trang chủ » Giải Pt Bậc 3 Online » Cách Giải Phương Trình Bậc 3 Nhanh Chóng - Gia Sư Trí Tuệ Việt

Có thể bạn quan tâm

Để giải phương trình bậc 3 có hai phương pháp giải, việc thứ nhất là giải bằng máy tính  và giải tay tùy thuộc vào phương trình đó mà ta áp dụng, và tùy theo bậc lớp học được phép sử dụng hay không. Bài này gia sư TTV chia sẽ cho tất cả các cách giải phương trình bậc 3 chuẩn mực nhất, nghiệm lẻ, hay một ẩn, tổng quát … và là trên máy tính. Chúng ta bắng đầu nào

Phương trình bậc 3 có dạng chuẩn sau

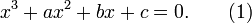
x^3 + ax^2 + bx +c = 0. \qquad (1)

Contents

  • 1 Phương pháp Cardano giải phương trình bậc 3
  • 2 Cách giải phương trình bậc 3 trên máy tính fx570es
  • 3 Cách giải phương trình bậc 3 tổng quát (mọi trường hợp)
    • 3.1 Cách giải phương trình bậc 2
    • 3.2 bộ tài liệu ôn thi đại học môn toán
    • 3.3 Công thức toán học trong word
    • 3.4 công thức lượng giác
    • 3.5 công thức diện tích tam giác
    • 3.6 công thức logarit
    • 3.7 công thức diện tích
    • 3.8 Quý phụ huynh có con em cần Gia Sư Dạy Kèm Tại Nhà xin liên hệ cho chúng tôi.
    • 3.9 Trung Tâm Chuyên Cung Cấp Gia Sư Dạy Kèm Tại Nhà Các Môn:
    • 3.10 TRUNG TÂM GIA SƯ TRÍ TUỆ VIỆT TP HCM

Phương pháp Cardano giải phương trình bậc 3

cach giai phuong trinh bac 3

cach giai phuong trinh bac 3

Chú ý rằng, có sáu giá trị u tìm được từ (4), vì có hai căn bậc ba ứng với hai dấu (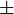\pm), và mỗi căn bậc ba có ba giá trị (một giá trị thực và hai tích của nó với 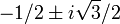-1/2 \pm i\sqrt{3}/2). Tuy nhiên, dấu của các căn phải chọn sao cho khi tính x, không gặp trường hợp chia cho không. Thứ nhất, nếu p = 0, thì chọn dấu của căn bậc hai sao cho u khác 0, i.e. u = \sqrt[3]{q}. Thứ hai, nếu p = q = 0, thì ta có x = −a/3.

Cách giải phương trình bậc 3 trên máy tính fx570es

cach giai phuong trinh bac 3 bang may tinh

Cách giải phương trình bậc 3 tổng quát (mọi trường hợp)

Đây là phần tóm tắt kết quả bài giải phương trình bậc ba: 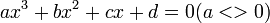 ax^3 + bx^2 + cx + d = 0 (a <>0)

Đặt các giá trị:

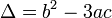
\Delta = b^2-3ac

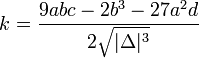
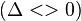
k = \frac{9abc-2b^3-27a^2d}{2\sqrt{|\Delta|^3}} (\Delta <> 0)

1) Nếu 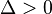\Delta > 0

1.1) |k| ≤ 1: Phương trình có ba nghiệm

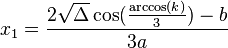
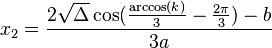
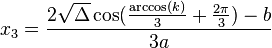
x_1 = \frac{2\sqrt{\Delta}\cos(\frac{\arccos(k)}{3})-b}{3a}x_2 = \frac{2\sqrt{\Delta}\cos(\frac{\arccos(k)}{3}-\frac{2\pi}{3})-b}{3a}x_3 = \frac{2\sqrt{\Delta}\cos(\frac{\arccos(k)}{3}+\frac{2\pi}{3})-b}{3a}

1.2) |k| > 1: Phương trình có một nghiệm duy nhất

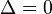x = \frac{\sqrt{\Delta}|k|}{3ak}\left(\sqrt[3]{|k|+\sqrt{k^2-1}}+\sqrt[3]{|k|-\sqrt{k^2-1}}\right)-\frac{b}{3a}2) Nếu \Delta = 0: Phương trình có một nghiệm bội

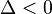x = \frac{-b+\sqrt[3]{b^3-27a^2d}}{3a}3) Nếu \Delta < 0 : Phương trình có một nghiệm duy nhất

x = \frac{\sqrt{|\Delta|}}{3a}\left(\sqrt[3]{k+\sqrt{k^2+1}}+\sqrt[3]{k-\sqrt{k^2+1}}\right)-\frac{b}{3a}

Trên là tất cả những gì liên quan đến cách giải phương trình bậc 3 để giúp các  gia sư môn Toán và cả học trò thống kê lại kiến thức tốt hơn, gần tết rồi day kem TTV xin chúc các bạn làm gia sư và học trò một năm mới an khang thịnh vượng

bài viết thuộc nguồn sở hữu của: Trung tâm gia sư TPHCM Trí Tuệ Việ

CÁC BÀI VIẾT LIÊN QUAN NHẤT CỦA CHÚNG TÔI

Cách giải phương trình bậc 2

bộ tài liệu ôn thi đại học môn toán

Công thức toán học trong word

công thức lượng giác

công thức diện tích tam giác

công thức logarit

công thức diện tích

Quý phụ huynh có con em cần Gia Sư Dạy Kèm Tại Nhà xin liên hệ cho chúng tôi.

Trung Tâm Chuyên Cung Cấp Gia Sư Dạy Kèm Tại Nhà Các Môn:

– Toán – Lý – Hóa – Sinh – Văn – Tiếng Anh…Từ Lớp 1 Đến 12, LTĐH – Anh Văn Giao Tiếp: Xuất Cảnh, Du Học, Buôn Bán………. – Luyện Thi: IELTS – TOELF – TOEIC… – Các thứ tiếng: Hoa(Trung) – Hàn – Nhật – Pháp… – Các môn năng khiếu: Vẽ – Đàn – Nhạc… – Tin học: Word, Excel, Eccess, PowerPoint… – Luyện viết chữ đẹp… – Tiếng việt cho người nước ngoài

Trung Tâm Dạy Kèm Tại Nhà các Quận 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 , Thủ Đức, Tân Bình, Tân Phú, Gò Vấp, Phú Nhuận, Bình Thạnh, Bình Tân, Nhà Bè, Hóc Môn.

Lưu ý: Trung Tâm sẽ cho gia sư dạy thử từ 1 – 2  buổi trước khi dạy chính thức để đảm bảo chất lượng gia sư của trung tâm.

Quý phụ huynh và các bạn gia sư có nhu cầu xin liên hệ:

TRUNG TÂM GIA SƯ TRÍ TUỆ VIỆT TP HCM

Điện Thoại : 0906 801 079 – 0932 622 625 (Thầy Huy – Cô Oanh)

Từ khóa » Giải Pt Bậc 3 Online