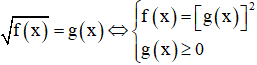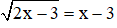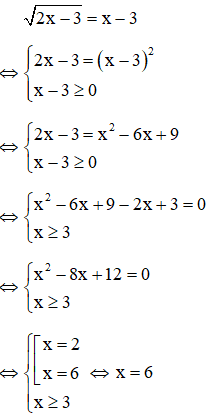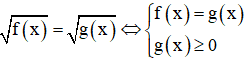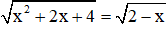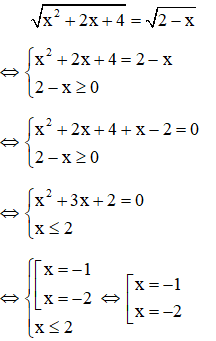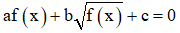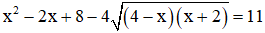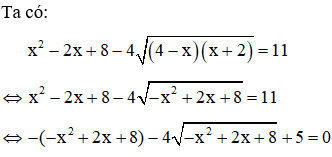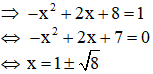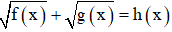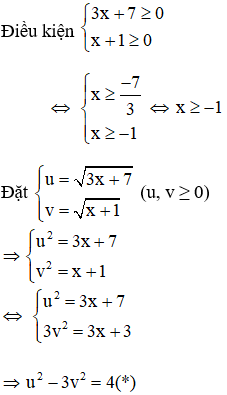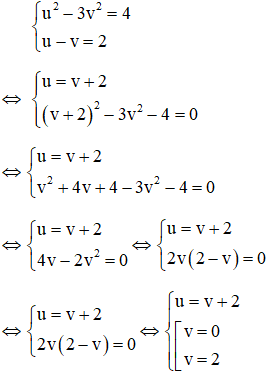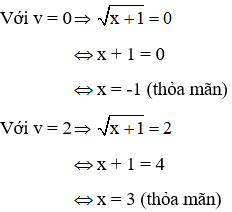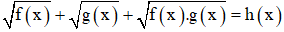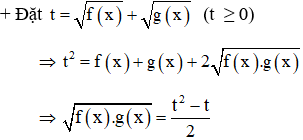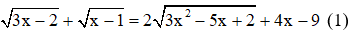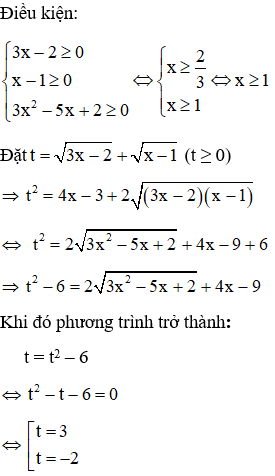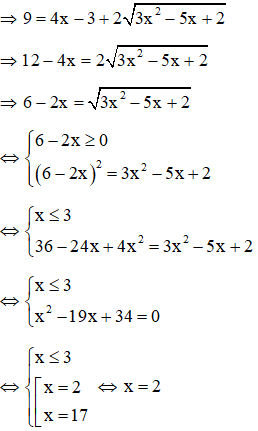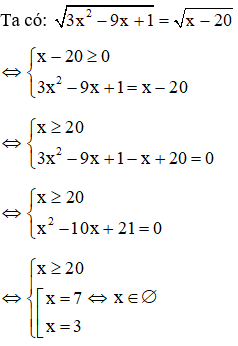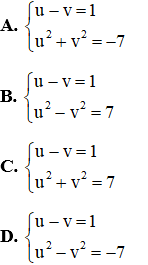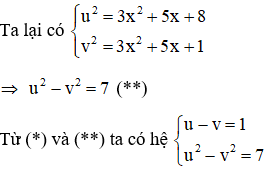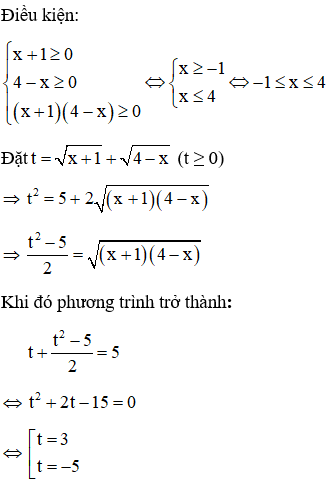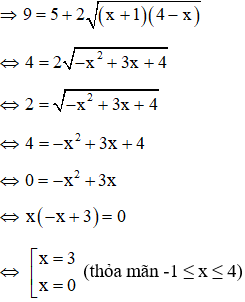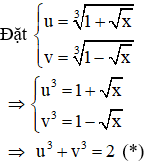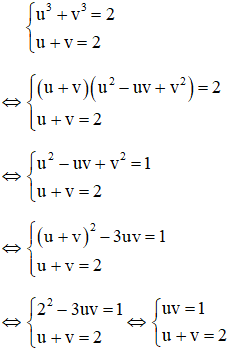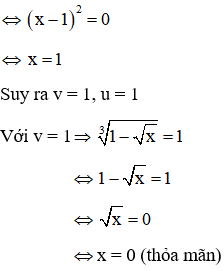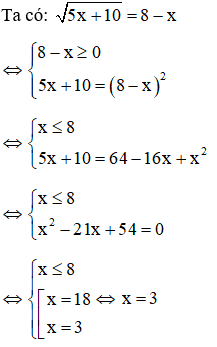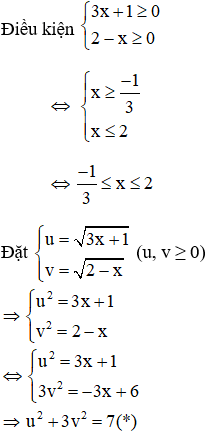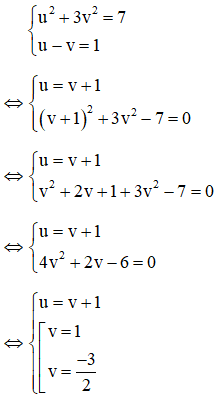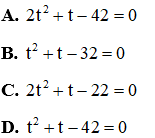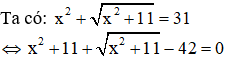Cách Giải Phương Trình Chứa Căn Thức Lớp 9 Cực Hay

Cách giải phương trình chứa căn thức lớp 9 cực hay

A. Phương pháp giải

Để giải phương trình chứa ẩn dưới dấu căn ta tìm cách khử dấu căn. Hai cách hay dùng là:

- Nâng hai vế của phương trình lên một lũy thừa

- Đặt ẩn phụ

Dạng 1:

Ví dụ:Giải phương trình

Giải

Vậy phương trình có một nghiệm x = 6

Dạng 2:

Chú ý: Điều kiện g(x) ≥ 0 có thể thay bởi f(x) ≥ 0

Ví dụ:Giải phương trình

Giải

Vậy phương trình có hai nghiệm x = -1, x = -2

Dạng 3:

Đặt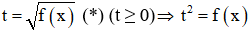. Khi đó phương trình đã cho trở thành: at2+ bt + c = 0

Giải phương trình trên tìm t thỏa mãn điều kiện t ≥ 0 rồi sau đó thay vào biểu thức (*) tìm x

Ví dụ:Giải phương trình

Giải

Đặt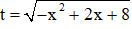 (*) (t ≥ 0) ⇒ t2= -x2+ 2x + 8. Khi đó phương trình đã cho trở thành: -t2- 4t + 5 = 0

Phương trình có a + b + c = -1 + (-4) +5 = 0 nên có 2 nghiệm

t = 1( thỏa mãn t ≥ 0); t = -5 ( không thỏa mãn t ≥ 0)

với t = 1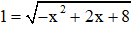 (ĐK: -x2+ 2x +8 ≥ 0)

Hai nghiệm tìm được thỏa mãn điều kiện

Vậy phương trình có hai nghiệm x = 1 ± √8

Dạng 4:

+ Đặt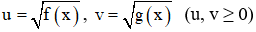 (u, v ≥ 0)

+ Đưa phương trình đã cho về hệ phương trình với hai ẩn là u, v

+ Giải hệ tìm u, v sau đó tìm x

Ví dụ:Giải phương trình 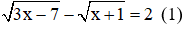(1)

Giải

Với việc đặt ẩn phụ như trên thì phương trình (1): u – v = 2(**)

Kết hợp (*) và (**) ta có hệ phương trình:

Ta có v = 0 và v = 2 đều thỏa mãn điều kiện v ≥ 0

Vậy phương trình có 2 nghiệm x =-1, x = 3

Dạng 5:

+ Đưa phương trình đã cho về hệ phương trình với ẩn là t

+ Giải phương trình tìm t, sau đó tìm x

Ví dụ:Giải phương trình

Giải

Với t = -2 (không thỏa mãn) ⇒ loại

Với t = 3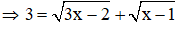(điều kiện x ≥ 1)

Ta thấy x = 2 thỏa mãn điều kiện x ≥1

Vậy phương trình có 1 nghiệm x = 2

B. Bài tập

Câu 1: Tổng các nghiệm của phương trình 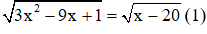(1) là

A.-3

B.2

C.10

D.không tồn tại

Giải

Vậy phương trình vô nghiệm

Đáp án là D

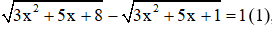
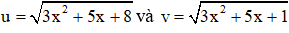
Câu 2: Cho phương trình (1), nếu đặtthì phương trình (1) trở thành hệ phương trình nào sau đây

Giải

Đặt(u, v ≥ 0)thì phương trình (1) trở thành: u – v = 1(*)

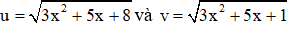
Đáp án đúng là B

Câu 3: Tích các nghiệm của phương trình 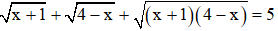(1) là

A.0

B.2

C.1

D.không tồn tại

Giải

Với t = -5 (không thỏa mãn)⇒ loại

Với t = 3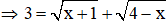(điều kiện -1≤ x ≤ 4)

Vậy phương trình có 2 nghiệm x = 0, x = 3

Suy ra tích các nghiệm bằng 0

Đáp án là A

Câu 4: Số nghiệm của phương trình 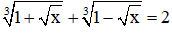(1) là

A.1

B.2

C.3

D.4

Giải

Điều kiện: x ≥ 0

Với việc đặt ẩn phụ như trên thì phương trình (1): u + v = 2(**)

Kết hợp (*) và (**) ta có hệ phương trình:

Theo vi-et ta có u, v là nghiệm của phương trình: x2– 2x + 1 = 0

Vậy phương trình có 1 nghiệm

Đáp án là A

Câu 5: Số nghiệm của phương trình 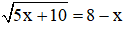là

A.0

B.1

C.2

D.3

Giải

Vậy phương trình có một nghiệm

Đáp án là B

Câu 6: Số nghiệm của phương trình 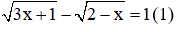là

A.1

B.2

C.3

D.4

Giải

Với việc đặt ẩn phụ như trên thì phương trình (1): u – v = 1(**)

Kết hợp (*) và (**) ta có hệ phương trình:

Ta có v = 1 thỏa mãn điều kiện v ≥ 0 nên nhận

Ta có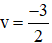 không thỏa mãn điều kiện v ≥ 0 nên loại

Với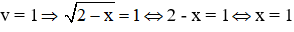(thỏa mãn)

Vậy phương trình có 1 nghiệm

Đáp án là A

Câu 7: Cho phương trình 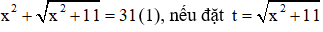thì phương trình (1) trở thành phương trình nào sau đây

Giải

Đặt. Khi đó phương trình đã cho trở thành: t2+ t - 42 = 0

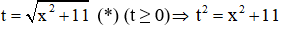
Đáp án đúng là D