Cách Giải Phương Trình Trùng Phương, Phương Trình Tích - Toán Lớp 9

1. Cách giải phương trình đưa về phương trình tích.

Phương pháp giải

• Bước 1: Biến đổi phương trình ban đầu bằng các phép biến đổi đại số (đặt nhân tử chung, sử dụng hằng đẳng thức, nhóm các hạng tử,...).

• Bước 2: Đưa phương trình về dạng phương trình tích A(x)⋅B(x)=0.

• Bước 3: Giải phương trình bằng cách cho từng nhân tử bằng 0, tức là A(x)=0 hoặc B(x)=0.

Ví dụ 1: Giải phương trình

a) (x - 3)(x2 - 3x + 2) = 0

b) x3 + 3x2 - 2x - 6 = 0

Lời giải:

a) (x - 3)(x2 - 3x + 2) = 0

⇔ x - 3 = 0 hoặc x2 - 3x + 2 = 0

+) x - 3 = 0 ⇔ x1 = 3

+) x2 - 3x + 2 = 0 ta thấy: a = 1; b = -3; c = 2 và a + b + c = 0 nên theo Vi-et ta có nghiệm x2 = 1; x3 = c/a = 2.

• Kết luận: Vậy phương trình đã cho có 3 nghiệm là: x1 = 3; x2 = 1; x3 = 2.

b) x3 + 3x2 - 2x - 6 = 0

⇔ x2(x + 3) - 2(x + 3) = 0

⇔ (x + 3)(x2 - 2) = 0

⇔ x + 3 = 0 hoặc x2 - 2 = 0

+) x + 3 = 0 ⇔ x1 = -3

+) x2 - 2 = 0 ⇔  ;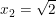 

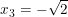
• Kết luận: Vậy phương trình đã cho có 3 nghiệm là: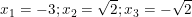

• Xem thêm: Cách giải phương trình chứa ẩn ở mẫu cực hay

* Ví dụ 2: Giải các phương trình

a) (3x2 – 5x + 1)(x2 – 4) = 0;

b) (2x2 + x – 4)2 – (2x – 1)2 = 0.

° Lời giải:

a) (3x2 – 5x + 1)(x2 – 4) = 0;

⇔ 3x2 – 5x + 1 = 0 hoặc x2 – 4 = 0

+)Giải: 3x2 – 5x + 1 = 0

- Có a = 3; b = -5; c = 1 ⇒ Δ = (-5)2 – 4.3 = 13 > 0

⇒ Phương trình có hai nghiệm: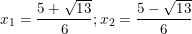 

+)Giải: x2 – 4 = 0

⇔ (x - 2)(x + 2) = 0

⇔ x = 2 hoặc x = -2.

• Kết luận: Vậy phương trình đã cho có 4 nghiệm là:

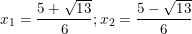 ; x3 = 2; x4 = -2

- Hay tập nghiệm của phương trình là: 

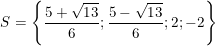
b) (2x2 + x – 4)2 – (2x – 1)2 = 0

⇔ (2x2 + x – 4 – 2x + 1)(2x2 + x – 4 + 2x – 1) = 0

⇔ (2x2 – x – 3)(2x2 + 3x – 5) = 0

⇔ 2x2 – x – 3 = 0 hoặc 2x2 + 3x – 5 = 0

+) Giải: 2x2 – x – 3 = 0

- Có a = 2; b = -1; c = -3 và thấy a – b + c = 0

⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 3/2.

+) Giải: 2x2 + 3x – 5 = 0

- Có a = 2; b = 3; c = -5 và thấy a + b + c = 0

⇒ Phương trình có hai nghiệm x = 1 và x = c/a = -5/2.

• Kết luận: Vậy phương trình đã cho có 4 nghiệm là: x1 = -1; x2 =  3/2; x3 = 1; x4 = -5/2.

- Hay tập nghiệm của phương trình là: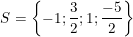 

• Xem thêm: Cách giải phương trình bâc 2 chứa ẩn ở mẫu cực hay 

2. Cách giải phương trình trùng phương ax4 +bx2 + c = 0 (a≠0).

Phương pháp giải 1: Đặt ẩn phụ

• Bước 1: Đặt ẩn phụ t=x2 với điều kiện t≥0.

• Bước 2: Thay t vào phương trình, ta được phương trình bậc hai theo t: at2+bt+c=0.

• Bước 3: Giải phương trình bậc hai theo t, sau đó đối chiếu với điều kiện t≥0.

  • Với mỗi nghiệm t thỏa mãn, ta giải phương trình x2=t để tìm nghiệm x.

• Bước 4: Kết luận số nghiệm của phương trình trùng phương.

Phương pháp giải 2: Giải trực tiếp bằng cách đưa về phương trình tích

• Biến đổi phương trình trùng phương bằng cách phân tích thành nhân tử để đưa về dạng A(x)⋅B(x)=0.

* Ví dụ 1: Giải các phương trình trùng phương:

a) x4 – 5x2 + 4 = 0

b) 2x4 – 3x2 – 2 = 0

c) 3x4 + 10x2 + 3 = 0

° Lời giải:

a) x4 – 5x2 + 4 = 0  (1)

- Đặt t = x2, điều kiện t ≥ 0.

- Khi đó (1) trở thành : t2 – 5t + 4 = 0 (2)

- Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0

⇒ Phương trình có hai nghiệm t1 = 1; t2 = c/a = 4

- Cả hai giá trị đều thỏa mãn điều kiện.

+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1;

+ Với t = 4 ⇒ x2 = 4 ⇒ x = 2 hoặc x = -2.

- Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.

b) 2x4 – 3x2 – 2 = 0; (1)

- Đặt t = x2, điều kiện t ≥ 0.

- Khi đó (1) trở thành : 2t2 – 3t – 2 = 0 (2)

- Giải (2) : Có a = 2 ; b = -3 ; c = -2 ⇒ Δ = (-3)2 - 4.2.(-2) = 25 > 0

⇒ Phương trình có hai nghiệm: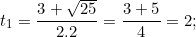  

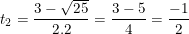
- Đối chiếu điều kiện t≥0 ta thấy chỉ có giá trị t1 = 2 thỏa mãn điều kiện.

+ Với t = 2 ⇒ x2 = 2 ⇒ x = √2 hoặc x = -√2;

- Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.

c) 3x4 + 10x2 + 3 = 0 (1)

- Đặt t = x2 , điều kiện t ≥ 0.

- Khi đó (1) trở thành : 3t2 + 10t + 3 = 0 (2)

- Giải (2): Có a = 3; b' = 5; c = 3 ⇒ Δ’ = 52 – 3.3 = 16 > 0

⇒ Phương trình có hai nghiệm phân biệt:

  

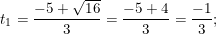
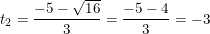
- Đối chiếu điều kiện t≥0 ta thấy cả 2 giá trị t1 = -1/3 <0 và t2 = -3<0 đều không thỏa điều kiện. Vậy phương trình (1) vô nghiệm.

* Ví dụ 2: Giải các phương trình trùng phương

a) 9x4 – 10x2 + 1 = 0 

b) 5x4 + 2x2 – 16 = 10 – x2

c) 0,3x4 + 1,8x2 + 1,5 = 0

d)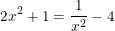 

° Lời giải:

a) 9x4 – 10x2 + 1 = 0 (1)

- Đặt t = x2, điều kiện t ≥ 0.

- Khi đó (1) trở thành : 9t2 – 10t + 1 = 0 (2)

+) Giải (2): Có a = 9 ; b = -10 ; c = 1; ta thấy a + b + c = 0

⇒ Phương trình (2) có nghiệm t1 = 1; t2 = c/a = 1/9.

- Cả hai nghiệm đều thỏa mãn điều kiện t≥0.

+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1.

+ Với t = 1/9 ⇒ x2 = 1/9 ⇒ x = 1/3 hoặc x = -1/3. 

• Kết luận: Vậy phương trình (1) có tập nghiệm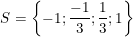 

b) 5x4 + 2x2 – 16 = 10 – x2

⇔ 5x4 + 2x2 – 16 – 10 + x2 = 0

⇔ 5x4 + 3x2 – 26 = 0 (1)

- Đặt t = x2 , điều kiện t ≥ 0.

- Khi đó (1) trở thành : 5t2 + 3t – 26 = 0 (2)

+ Giải (2): Có a = 5 ; b = 3 ; c = -26 ⇒ Δ = 32 – 4.5.(-26) = 529 > 0

⇒ Phương trình có hai nghiệm phân biệt:

 

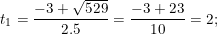
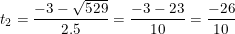
- Đối chiếu điều kiện chỉ có t1 thỏa điều kiện, nên:

+ Với t = 2 ⇒ x2 = 2 ⇒ x = √2 hoặc x = -√2.

⇒ Kết luận: Vậy phương trình (1) có tập nghiệm S = {-√2; √2}.

c) 0,3x4 + 1,8x2 + 1,5 = 0 (1)

- Đặt t = x2, điều kiện t ≥ 0.

- Khi đó, (1) trở thành : 0,3t2 + 1,8t + 1,5 = 0 (2)

+ Giải (2) : có a = 0,3 ; b = 1,8 ; c = 1,5; ta thấy a – b + c = 0

⇒ Phương trình có hai nghiệm t1 = -1 và t2 = -c/a = -5.

- Đối chiếu với điều kiện t ≥ 0 thấy cả hai nghiệm đều không thỏa.

⇒ Vậy phương trình (1) vô nghiệm.

d)  (*)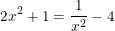

- Điều kiện xác định: x ≠ 0.

- Quy đồng, khử mẫu ta được:

(*) ⇔ 2x4 + x2 = 1 – 4x2

 ⇔ 2x4 + x2 + 4x2 – 1 = 0

 ⇔ 2x4 + 5x2 – 1 = 0 (1)

- Đặt t = x2, điều kiện t > 0 (do x ≠ 0).

- Khi đó (1) trở thành : 2t2 + 5t – 1 = 0 (2)

+ Giải (2): Có a = 2 ; b = 5 ; c = -1 ⇒ Δ = 52 – 4.2.(-1) = 33 > 0

⇒ Phương trình có hai nghiệm phân biệt:

  

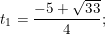
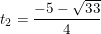
- Đối chiếu với điều kiện t >0 thấy có nghiệm t1 thỏa mãn, nên:

+ Với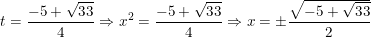 

• Kết luận: Vậy phương trình có tập nghiệm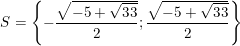

3. Bài tập vận dụng

* Bài 1: Giải các phương trình sau

a) x4 - 22x2 - 8x +77 = 0

b) x4 - 6x3 + 8x2 + 2x - 1 = 0

c) x4 + 2x3 - 5x2 + 6x - 3 = 0

* Bài 2: Giải các phương trình sau

a) 5x4 + 3x2 - 2 = 0

b) x4 - 5x2 + 6 = 0

c) 2x4 - 3x2 - 2 = 0