Cách Nhẩm Nghiệm Phương Trình Bậc Hai

• Trang chủ
• Công nghệ
  • Phần mềm toán học
  • Tin học văn phòng
• Giáo dục
  • Dạy và học toán
  • Nghiệp vụ sư phạm
  • Thi vectơ
    • Thông tin chi tiết
      • Thể lệ cuộc thi
      • Danh sách bài dự thi
      • Tài trợ cuộc thi
      • Quảng bá cuộc thi
      • Hỏi đáp về cuộc thi
    • Công tác chấm
      • Ngày chấm đầu tiên
      • Kết quả chấm
    • Công bố giải thưởng
    • Hình ảnh buổi lễ trao giải
    • Thư cảm ơn
      • của người giành Giải Nhất
      • của Ban tổ chức
    • Các lời giải tiêu biểu
  • Làm toán
• Thư viện
• Giới thiệu
  • Hợp tác
  • Liên hệ
• Tải xuống
• Sitemap

Home » Làm toán » Cách nhẩm nghiệm phương trình bậc hai Cách nhẩm nghiệm phương trình bậc hai

Vận dụng định lý Vi-et để nhẩm nghiệm phương trình bậc hai là một kĩ năng cần đạt đối với các bạn học sinh lớp 101. Trong nhiều trường hợp, thậm chí với hệ số chứa căn hay tham số, nếu biết nhẩm nghiệm thì học sinh sẽ nhanh chóng tìm được nghiệm mà không cần phải nháp hay sử dụng máy tính. Tuy nhiên, trong SGK Đại số 10 thì mục này chỉ được giới thiệu sơ lược và không có nhiều bài tập vận dụng cho việc tính nhẩm. Đó là lí do bài viết này ra đời. [latexpage]

1. Cơ sở tính nhẩm
2. Các dạng thường gặp
   • Loại 1: a = 1, b = tổng, c = tích
   • Loại 2: a + b + c = 0, a – b + c = 0
   • Loại 3: Hai nghiệm là nghịch đảo của nhau
   • Loại 4: Các loại khác
3. Một số ví dụ vận dụng
4. Bình luận

1. Cơ sở tính nhẩm

Cơ sở tính nhẩm xuất phát từ định lí Vi-ét quen thuộc sau:2

Định lí Vi-ét

Định lý gồm 2 phần, thuận và đảo:

* Nếu phương trình trình $ax^2 + bx + c = 0\ (a\ne 0)$ có hai nghiệm $x_1, x_2$ thì

$x_1 + x_2 = -\frac{b}{a}; x_1 x_2 = \frac{c}{a}$

* Ngược lại, nếu hai số $u$ và $v$ có tổng $u+v=S$ và tích $uv=P$ thì $u$ và $v$ là các nghiệm của phương trình

$x^2 – Sx + P = 0$

2. Các dạng tính nhẩm thường gặp

Từ phần đảo, dễ dàng suy ra các kết quả sau.

Loại 1: a = 1, b = tổng, c = tích

* Nếu phương trình có dạng $x^2 – (u+v)x + uv = 0$ thì phương trình đó có hai nhiệm $u$ và $v$.

* Nếu phương trình có dạng $x^2 + (u+v)x + uv = 0$ thì phương trình có hai nghiệm $-u$ và $-v$

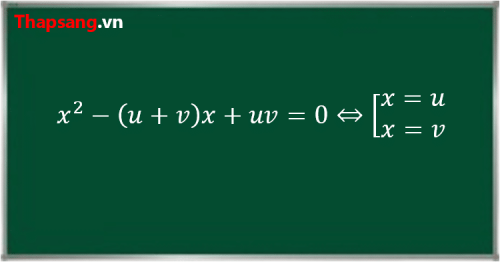
Nếu a bằng 1, -b là tổng hai số và c là tích hai số đó thì phương trình bậc hai nhận hai số đó làm nghiệm

Tóm lại:

$x^2 – (u+v)x + uv = 0\Rightarrow x_1 = u, x_2 = v\ (1)$

$x^2 + (u+v)x + uv = 0\Rightarrow x_1 = -u, x_2 = -v$

Như vậy, với loại này bạn cần thực hiện 2 phép nhẩm: “Phân tích hệ số $c$ thành tích và $b$ thành tổng”. Trong hai phép nhẩm đó, bạn nên nhẩm hệ số $c$ trước rồi kết hợp với $b$ để tìm ra hai số thỏa mãn tích bằng $c$ và tổng bằng $b$.

Khi tiến hành, bạn nhẩm trong đầu như sau:

Tích của hai nghiệm bằng $c$, mà tổng lại bằng $b$

Ví dụ phương trình

* $x^2 – 5x + 6 = 0$

Nhẩm: “Tích của hai nghiệm bằng 6, mà tổng lại bằng 5”. Hai số đó là: 2 và 3 vì 6 = 2.3 và 5 = 2 + 3. Vậy phương trình có hai nghiệm $x=2,x=3$

* $x^2 – 7x + 10 = 0$

Nhẩm: “Tích của hai nghiệm bằng 10, mà tổng lại bằng 7”. Hai số đó là: 2 và 5 vì 10 = 2.5 và 7 = 2 + 5. Vậy phương trình có hai nghiệm $x=2,x=5$

Loại 2: a + b + c = 0 và a – b + c = 0

* Nếu thay $v=1$ vào (1) thì bạn sẽ có trường hợp nhẩm nghiệm quen thuộc $a + b + c = 0$, với $a=1, b=-(u+1), c=u$.

* Nếu thay $v=-1$ vào (1) thì bạn sẽ có trường hợp nhẩm nghiệm $a – b + c = 0$, với $a=1, b=-(u-1), c=-u$.

Do loại này đã quá quen thuộc với bạn, nên bài viết không xét các ví dụ cho trường hợp này mà tập trung vào loại 1 và loại 3.

Loại 3: Hai nghiệm là nghịch đảo của nhau

Nếu $u\ne 0$ và $v=\frac{1}{u}$ thì phương trình (1) có dạng

$x^2 – (u+\frac{1}{u})x + u.\frac{1}{u} = 0\Leftrightarrow u.x^2 – (u^2 + 1)x + u = 0$

khi đó phương trình có hai nghiệm là nghịch đảo của nhau $x=u,x=\frac{1}{u}$. Đây cũng là trường hợp hay gặp khi giải toán. Ví dụ phương trình

* $2x^2 – 5x + 2 = 0$ có hai nghiệm $x=2,x=\frac{1}{2}$

* $3x^2 – 10x + 3 = 0$ có hai nghiệm $x=3,x=\frac{1}{3}$

Loại 4: Những trường hợp còn lại

Với một phương trình có hệ số $a\ne 1$ mà không phải loại 2, loại 3 thì bạn nên chia cả hai vế cho $a$, quy về loại 1 để nhẩm. Còn nếu vẫn không nhẩm được thì bạn biết phải làm gì rồi chứ 😀3

3. Một số ví dụ vận dụng

Ví dụ 1. Phương trình

* $x^2 – 8x + 12 = 0$ có hai nghiệm $x=2,x=6$ vì 12 = 2.6 và 8 = 2 + 6

* $x^2 – 7x + 12 = 0$ có hai nghiệm $x=3,x=4$ vì 12 = 3.4 và 7 = 3 + 4

* $x^2 – x – 12 = 0$ có hai nghiệm $x=-3,x=4$ vì -12 = (-3).4 và 1 = (-3) + 4

* $x^2 + x – 12 = 0$ có hai nghiệm $x=3,x=-4$ vì -12 = 3.(-4) và -1 = 3 + (-4)

* $x^2 – 4x – 12 = 0$ có hai nghiệm $x=-2,x=6$ vì -12 = (-2).6 và 4 = (-2) + 6

* $x^2 + 4x – 12 = 0$ có hai nghiệm $x=2,x=-6$ vì -12 = 2.(-6) và -4 = 2 + (-6)

Ví dụ 2. Phương trình

* $x^2 -(m+4)x+ 3m+3 = 0$4 có hai nghiệm $x=3,x=m+1$, vì nó có dạng

$x^2 -[(m+1)+3]x+ 3(m+1) = 0$

* $x^2 -(2m+1)x+m^2 + m = 0$ có hai nghiệm $x=m,x=m+1$, vì nó có dạng

$x^2 -[m+(m+1)]x+ m(m+1) = 0$

* $x^2 -2mx+m^2-1 = 0$ có hai nghiệm $x=m-1,x=m+1$, vì nó có dạng

$x^2 -[(m-1)+(m+1)]x+ (m-1)(m+1) = 0$

Ví dụ 3. Phương trình

* $\sqrt{2}x^2 – (2\sqrt{2}+1)x + 2 = 0$ có hai nghiệm $x=2,x=\frac{1}{\sqrt{2}}$5

* $x^2 – (\log{6})x + \log{2}.\log{3} = 0$ có hai nghiệm $x=\log{2},x=\log{3}$6

* $x^2-(3-2^x )x+2(1-2^x )=0\Leftrightarrow x=2,x=1-2^x$7

4. Bình luận

Khi mới làm quen với tính nhẩm, có thể bạn sẽ gặp một chút khó khăn, nhưng đừng vì thế mà ngại khó và bỏ cuộc. Hãy tưởng tượng thành quả mà tính nhẩm đem lại cho bạn là “không đếm được” so với những “trở ngại đếm được” mà bạn đang phải đối mặt. Bạn sẽ có thêm động lực tiến lên.

[tsquote mess=”Đừng cảm thấy tiếc vì bụi hoa hồng có gai mà hãy vui vì trong bụi gai có hoa hồng.” author=’Abraham Lincoln‘] Th11 30, 2013Thapsang.vn

Có thể bạn muốn xem

Câu 5 - hình học không gian, năm nay dễ hơn năm ngoái

Thiểu số theo đa số

Câu 4 - tính tích phân, năm ngoái khó hơn năm nay

Câu 8 - hình học tọa độ trong không gian, năm nay dễ quá

1. Theo Chuẩn kiến thức, kĩ năng môn Toán lớp 10, NXB Giáo dục Việt Nam, 2009, trang 36 [↩]
2. “Trong toán học, định lý Viète hay công thức Viète (phiên âm tiếng Việt là Vi-ét), do nhà toán học Pháp François Viète tìm ra, nêu lên mối quan hệ giữa các nghiệm của một phương trình đa thức (trong trường số phức) và các hệ số của nó” – Theo Wikipedia. [↩]
3. Lấy giấy nháp và máy tính ra chứ còn làm gì nữa [↩]
4. Bạn mà tính Delta để giải phương trình này thì sẽ có một sự mệt không hề nhẹ đấy! 😀 Vì phải xét dấu để khử dấu GTTĐ do Delta bằng |m – 4| [↩]
5. Khi học về phương trình lượng giác ở lớp 11, bạn sẽ hay gặp các phương trình bậc hai mà nghiệm của nó có chứa căn 2 hay căn 3 [↩]
6. Kí hiệu “log” đọc là logarit cơ số 10, bạn sẽ gặp nó khi học Giải tích lớp 12 [↩]
7. Bạn có thể giải phương trình này bằng phương pháp đặt ẩn phụ không hoàn toàn. Muốn ra đáp số cuối cùng, bạn phải học hết HK1 lớp 12 [↩]

Cách tính nhẩm số tổ hợpHỏi đáp: Cách tính một logarit theo các logarit đã choComments: 32

1. Minhnd Ngocminh12 years ago

   Trần Ngọc Minh đã đọc bài này.

   ReplyCancel
2. Nguyễn Thế Phúc12 years ago

   Nguyễn Thế Phúc đã đọc bài này :v

   ReplyCancel
3. Nguyễn Thế Phúc12 years ago

   Có một chi tiết khó hiểu về phần đảo của định lý Vi-ét được ghi trong Tài liệu hướng dẫn thực hiện chuẩn kiến thức, kĩ năng ở trang 37. Sau khi trình bày nội dung phần đảo, tài liệu này có bổ sung thêm: "(điều kiện: S^2 – 4P >= 0)"

   Điều kiện này là thừa, vì nếu đã tồn tại u và v sao cho u + v = S và u.v = P thì S^2 – 4P = (u + v)^2 – 4uv = (u – v)^2 >=0 rồi. Sao phải cần điều kiện gì nữa?

   ReplyCancel
   • ahuhu8 years ago

     thật ra mình sử dụng thêm cũng được thừa thì kệ đi

     ReplyCancel
4. Minhnd Ngocminh12 years ago

   Trần Ngọc Minh Like this idea 😀

   ReplyCancel
5. Nguyễn Thế Phúc11 years ago

   Hôm nay tận mắt thấy 3 cháu học sinh lớp 12 giải phương trình bậc hai $x^2-6x+9=0$ ra đáp số 2 nghiệm là $x=1,x=3$.

   Những điều trông thấy mà đau đớn lòng!! 🙁

   ReplyCancel
6. Minhnd Ngocminh11 years ago

   Chắc tại anh cấm trẻ sử dụng MTCT rồi?

   ReplyCancel
7. Nguyễn Thế Phúc11 years ago

   Minhnd Ngocminh Lớp 12 anh không cấm, thậm chí hướng dẫn chọn mua máy nào cho phù hợp.

   ReplyCancel
8. Tâm Lê11 years ago

   Thông thường e hay xài loại 2 để nhẩm một nghiệm 1 hoặc -1 và nghiệm còn lại.

   ReplyCancel
9. Nguyễn Thế Phúc11 years ago

   Loại 1 và 3 cũng rất hay gặp. Em thử thống kê mà xem, tần số gặp sẽ cao đấy.

   ReplyCancel
10. Nguyễn Thế Phúc11 years ago

    Một số phương trình bậc hai chứa 2 ẩn có thể đưa về tích dễ dàng mà không cần tính delta. Ví dụ, bạn sẽ đưa phương trình sau thành tích như thế nào?

    $(x+y)(2x-y)+4=-6x-3y$

    ReplyCancel
11. Tâm Lê11 years ago

    Cách nhóm đưa về tích phải không ạ.

    ReplyCancel
12. Nguyễn Thế Phúc11 years ago

    Tâm Lê Không, em suy nghĩ thêm nhé. Không dễ nhìn ra nhân tử chung để nhóm, nên nếu cứ thử biến đổi mà chưa định hướng được nhân tử chung thì thành ra là mò mẫm. 🙂

    ReplyCancel
13. Nguyễn Thế Phúc11 years ago

    Hôm trước mình có nói rằng có thể đưa phương trình bậc 2 hai ẩn: $(x+y)(2x-y)+4=-6x-3y$ thành tích. Bây giờ, nếu bạn thay 2 ẩn $x,y$ trong phương trình lần lượt bằng các hàm bậc nhất của cùng 1 đối số chẳng hạn $sin x, cos x$ thì bạn sẽ thu được một phương trình lượng giác có thể đưa về tích:

    $(sin x + cos x)(2sin x – cos x) + 4 = -6sin x – 3sin x$

    Bạn đã biết thêm một "sáng tạo" các phương trình lượng giác 😀

    ReplyCancel
14. Anh Nguyễn10 years ago

    cho em hỏi ngu xíu: phươg trìh $ x^2 – (log6)x + log2.log3 = 0 $ có nghiệm log2 và log3. từ đâu ra hai nghiệm đó vậy? :3

    ReplyCancel
15. Nguyễn Thế Phúc10 years ago

    Vì log 2 + log 3 = log 6 nên phương trình có thể viết dưới dạng:

    $x^2 – (log 2 + log 3)x + log2.log3 = 0$ do đó pt có hai nghiệm log2 và log3.

    PS: Đừng ngại hỏi, hãy luôn đặt câu hỏi.

    ReplyCancel
16. Thái Nguyễn10 years ago

    bài viết quá hay về giải phương trình

    ReplyCancel
17. tội phạm đặc biệt10 years ago

    cho em hỏi phương trình này làm thế nào vậy ạ: 2x^2=2x-8=0

    ReplyCancel
18. Nguyễn Thế Phúc10 years ago

    Phương trình của em thừa 1 dấu bằng?

    ReplyCancel
19. Dũng Lê10 years ago

    Toàn mấy quảng cáo chẳng ra gì!!! Làm ơn bớt giùm!!! Ngừng đi

    ReplyCancel
20. Nguyễn Thế Phúc10 years ago

    Xin lỗi vì các quảng cáo đã làm bạn khó chịu.

    Cảm ơn bạn đã click vào các quảng cáo, mỗi click đó của bạn đều rất ý nghĩa với chúng tôi. Số tiền chúng tôi nhận được từ mỗi click của bạn có thể rất rất nhỏ (0,01-0,02$), nhưng chúng giúp chúng tôi tiếp tục duy trì website này hoạt động và giữ được các bài viết đến được với nhiều người hơn.

    Một lần nữa, cảm ơn bạn!

    ReplyCancel
21. Phan Thị Thanh Huệ10 years ago

    Lưu Thị Thu Hà có cái này thì thứ tư ok

    ReplyCancel
22. Phan Thị Thanh Huệ10 years ago

    Lưu Thị Thu Hà đọc thì nhớ rep

    ReplyCancel
23. Den Uoc Mo Ngon9 years ago

    VERY GOOD

    ReplyCancel
24. Den Uoc Mo Ngon9 years ago

    that tiet khi sai mot cai o dang 3

    ReplyCancel
25. Cứ Đợi Đi Em9 years ago

    con nữa không thầy ít quá thầy ạ

    ReplyCancel
26. Cứ Đợi Đi Em9 years ago

    mà thầy ơi tải về ở trỗ lào vậy thầy

    ReplyCancel
27. Nguyễn Thế Phúc9 years ago

    Hiện tại blog của thầy chưa hỗ trợ tính năng tải về em ạ.

    PS: Dù là bình luận vui, nhưng vẫn phải viết đúng chính tả nhé. "Chỗ nào", not "trỗ lào" 🙂

    ReplyCancel
28. Mỹ Hà Võ Thị9 years ago

    Thầy ơi ghi rõ loại 2 a+b+c=0 đi thầy.. lâu rồi nên quên cách tính

    ReplyCancel
29. vy4 years ago

    để nhẩm nghiệm cho 1 phương trình có căn + căn= đa thức thì sao ạ

    ReplyCancel
    • Thapsang.vn4 years ago

      Thông thường sẽ có dạng tổng quát hoặc thử nghiệm nguyên (hoặc đặc biệt, dễ thấy).

      ReplyCancel
30. kn3 years ago

    thầy ơi nhẩm no loại 3 khó hiểu quá ạ:((

    ReplyCancel

Để lại một bình luận Hủy

Thapsang.vn

Chào bạn, Thapsang.vn – nơi chia sẻ các thông tin, kiến thức bổ ích về giáo dục và công nghệ, hoạt động từ 10/2012 đến nay. Hi vọng bài viết này có ích cho bạn và mong nhận được nhiều phản hồi của bạn. Cảm ơn bạn đã đọc bài viết!

12 years ago 32 Comments Làm toánLớp 10, Cách tính nhẩm, Phương trình bậc hai142,998

Series nổi bật

• _Tool for Teaching Logbook
• _Tool for Google Admin
• _Tool for Google Forms 1905
• Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
• Cách tính logarit
• Cuộc thi giải toán vectơ bằng nhiều cách

Bài viết gần đây

• Điều 15 của TT 19 có thể khiến giáo viên “vô cảm” và nhà trường “bất lực” 28/09/2025
• Tạo file pdf thân thiện trên thiết bị di động từ file word 08/09/2025
• Ngừng tư vấn tuyển sinh vào lớp 10 29/05/2025

Bình luận gần đây

• Khách trong Cách tính nhẩm số tổ hợp
• Vũ trong Cách xác định hướng của tích vectơ (Tích có hướng)
• An trong Tính chất của ba số hạng liên tiếp trong một cấp số
• Khách trong Cách xác định hướng của tích vectơ (Tích có hướng)

Chuyên mục

• Công nghệ (27)
• Dạy và học toán (32)
• Giáo dục (19)
• Google Workspace (13)
• Làm toán (13)
• Lập trình (3)
• Nghiệp vụ sư phạm (4)
• Phần mềm toán học (5)
• Thi giải toán vectơ (12)
• Thi vào 10 (3)
• Tin học văn phòng (13)
• Tool for Google Admin (3)
• Tool for Google Forms 1905 (3)

Tags

Lớp 12Google Apps ScriptMS WordCách phân tíchMS Word 2010Khẩu quyếtThi THPT Quốc Gia 2019Tình huống có vấn đềLogaritSai lầm thường gặpLớp 11ChromeChuyển đổi sốKhối AMôn ToánGmailPhổ điểm thiSo sánh đề thi 2013 với 2012Google classroomThi THPT Quốc Gia 2018Luyện thi Đại học - Cao đẳngwindowsSMASPhương trình mũGTNNLũy thừaTại saoCách gõ công thức toánQuy tắc tính logaritGTLNShutdown TimerGgAdmin1Cách vẽ hìnhTop điểm 10Kỹ thuật mở bàiLogarit hóacppGợi động cơCách vận dụngMicrosoft ExcelCách vào bàiMục tiêu giáo dụcCách tính nhẩmDẫn nhậpGVCN

Tra cứu

Tra cứu Chọn tháng Tháng 9 2025 (2) Tháng 5 2025 (3) Tháng 4 2025 (1) Tháng 8 2024 (1) Tháng mười một 2023 (1) Tháng 5 2023 (1) Tháng 4 2023 (1) Tháng 2 2023 (2) Tháng 1 2023 (1) Tháng mười một 2022 (1) Tháng 7 2022 (2) Tháng 6 2022 (5) Tháng 12 2021 (1) Tháng 10 2021 (10) Tháng 9 2021 (4) Tháng 8 2021 (1) Tháng 7 2021 (2) Tháng 6 2021 (3) Tháng 1 2021 (2) Tháng 9 2020 (1) Tháng 2 2020 (1) Tháng 10 2019 (3) Tháng 9 2019 (1) Tháng 8 2019 (1) Tháng 7 2019 (7) Tháng mười một 2018 (1) Tháng 10 2018 (1) Tháng 8 2018 (3) Tháng 7 2018 (1) Tháng 1 2018 (1) Tháng mười một 2017 (1) Tháng 10 2017 (2) Tháng 9 2017 (3) Tháng 8 2017 (1) Tháng mười một 2016 (3) Tháng 4 2016 (3) Tháng 3 2016 (2) Tháng 5 2015 (1) Tháng 1 2015 (2) Tháng 12 2014 (1) Tháng 10 2014 (4) Tháng 9 2014 (2) Tháng 8 2014 (3) Tháng 6 2014 (2) Tháng 5 2014 (3) Tháng 4 2014 (2) Tháng 1 2014 (2) Tháng 12 2013 (2) Tháng mười một 2013 (6) Tháng 10 2013 (4) Tháng 9 2013 (12) Tháng 8 2013 (8) Tháng 7 2013 (7) Tháng 6 2013 (4) Tháng 5 2013 (2) Tháng 10 2012 (3)

Quyên góp

Thapsang.vn cần sự ủng hộ của bạn để hoạt động. Cảm ơn bạn!