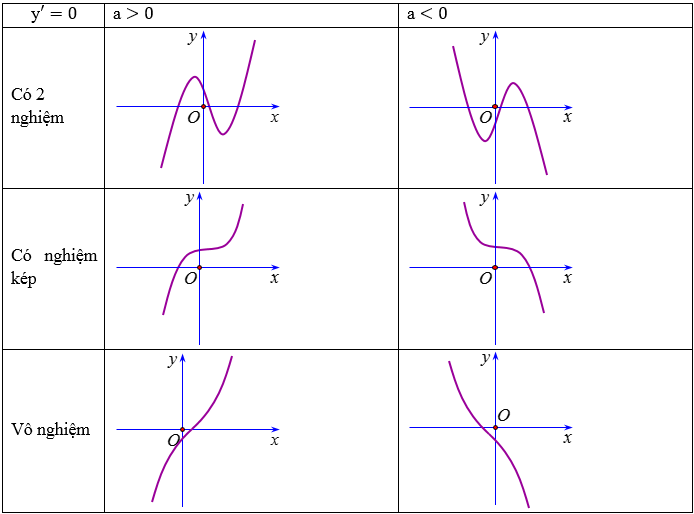Cách Nhận Dạng đồ Thị Hàm Số Bậc 3 Chi Tiết

Cách nhận dạng đồ thị hàm số bậc 3

A. Phương pháp giải & Ví dụ

Các dạng đồ thị của hàm số bậc 3 y = ax3 + bx2 + cx + d (a ≠ 0)

Đồ thị hàm số có 2 điểm cực trị nằm 2 phía so với trục Oy khi ac < 0

Đồ thị hàm số bậc ba luôn nhận điểm uốn làm tâm đối xứng

Ví dụ minh họa

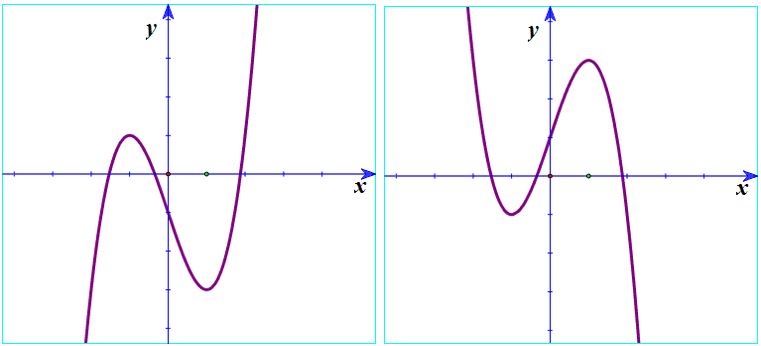
Ví dụ 1: Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. y = x3 - 3x + 1.

B. y = -x3 + 3x2 + 1.

C. y = x3 - 3x2 + 3x + 1.

D. y = -x3 - 3x2 - 1.

Hướng dẫn

Nhìn dạng đồ thị thấy a > 0 , suy ra loại B, D.

Mặt khác hàm số không có cực trị nên loại A.

Chọn C.

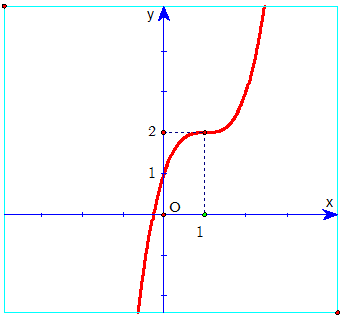
Ví dụ 2: Cho hàm số bậc 3 có dạng: y = f(x) = ax3 + bx2 + cx + d.

Hãy chọn đáp án đúng?

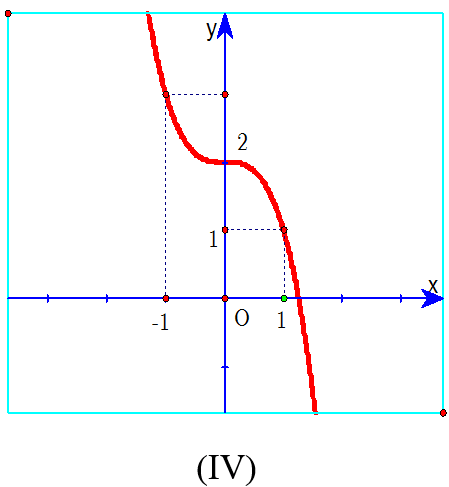
A. Đồ thị (IV) xảy ra khi a > 0 và f'(x) = 0 có nghiệm kép.

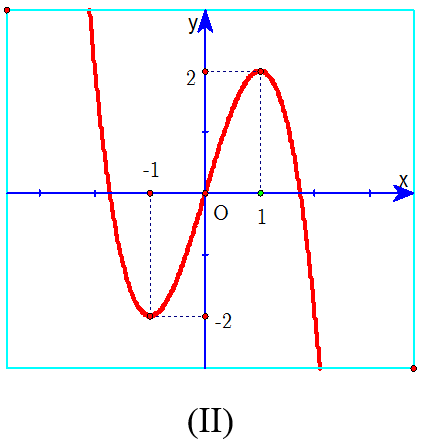
B. Đồ thị (II) xảy ra khi a ≠ 0 và f'(x) = 0 có hai nghiệm phân biệt.

C. Đồ thị (I) xảy ra khi a < 0 và f'(x) = 0 có hai nghiệm phân biệt.

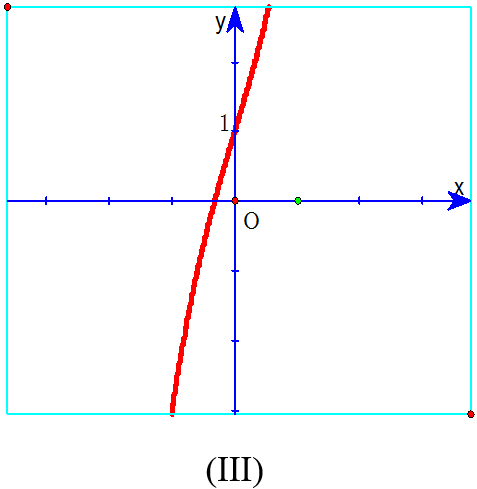
D. Đồ thị (III) xảy ra khi a > 0 và f'(x) = 0 vô nghiệm.

Hướng dẫn

Hàm số của đồ thị (II) có a < 0 nên điều kiện a ≠ 0 chưa đảm bảo. Do đó loại phương án B.

Hàm số của đồ thị (I) có a > 0 nên loại luôn phương án C.

Hàm số của đồ thị (IV) có a < 0 nên loại luôn phương án A.

Chọn D.

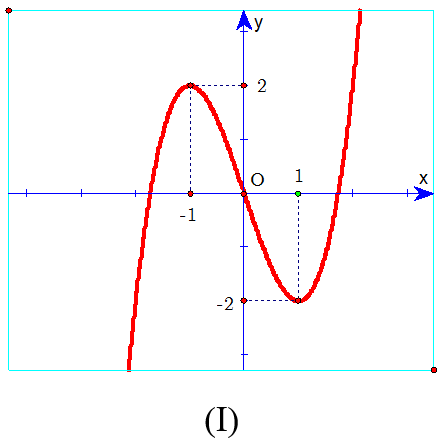
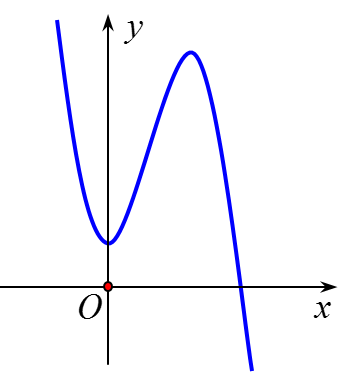
Ví dụ 3: Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ bên.

Mệnh đề nào dưới đây đúng?

A. a < 0,b > 0,c > 0,d > 0.

B. a < 0,b < 0,c = 0,d > 0.

C. a > 0,b < 0,c > 0,d > 0.

D. a < 0,b > 0,c = 0,d > 0.

Hướng dẫn

Từ hình dáng đồ thị ta suy ra hệ số a < 0,d > 0 loại đáp án C.

Ta có: y' = 3ax2 + 2bx + c

Vì hàm số đạt cực tiểu tại điểm x = 0 nên y'(0) = 0 ⇒ c = 0 loại đáp án A.

Khi đó: y' = 0 ⇔ 3ax2 + 2bx = 0 ⇔ x = 0 hoặc x = -2b/3a

Do hoành độ điểm cực đại dương nên -2b/3a > 0, mà a < 0 ⇒ b > 0.

Chọn D.