Cách Tìm Cực Trị Có điều Kiện - Học 3 Giây

Trong bài viết này mình sẽ nói về cách để tìm cực trị của một hàm số, nhưng không phải như bình thường mà ta cần tìm và phải suy xét điều kiện thêm kèm. Đó là hướng của bài ngày hôm chúng ta sẽ nắm bắt. Bây giờ mời các bạn xem ngay phần hướng dẫn chi tiết cách thực hiện bên dưới.

Cách tìm cực trị có điều kiện

Công thức đạo hàm sẽ sử dụng: (x^a)’=(a-1)x^(a-1), a’ = 0, x’=1.

Nhắc lại đạo hàm riêng: f(x,y)=f’x(x,y) và f’y(x,y) (cấp 1); f”xx(x,y), f”xy(x,y), f”yy(x,y) (cấp 2).

Ký hiệu toán học sử dụng trong bài: λ (Lambda).

Nối đến tìm cực trị ta phải nghĩ ngay đến tìm min và max dịch sang tiếng việt là số nhỏ nhất và lớn nhất. Rồi cách tìm cực trị như sau:

Mỗi bài toán về tìm cực trị nó sẽ chức 2 thông tin quan trọng để làm bài này. Thông tin thức nhất là một cái hàm cho trước và thông tin thứ hai là điều kiện.

Bước 1: Đặt 2 hàm g(x,y) và L(x,y) mà ở đó hàm g(x,y) chính là phương trình điều kiện còn hàm L(x,y) được viết dựa vào công thức sau L(x,y)=f(x,y) + λ(g(x,y)). Sau đó ta tiến hành đạo hàm riêng hàm L(x,y), chỉ cần đạo hàm cấp 1, cấp 2 ta tới bước 3 thì mới tính đạo hàm tiếp.

Bước 2: Tìm P thỏa (*) 3 điều: f’x=0, f’y=0, g=0. Nhờ 3 điều này ta sẽ rút ra được x,y và λ, tới lúc đó ta tiến hành viết tọa độ điểm P1(x1,y1), P2(x2,y2) tùy thuộc vào số lượng x và y tìm được. Theo mình thấy mỗi bài toán tìm cực trị có điều kiện như dạng này thì thường cho tối đa 2 điểm x và 2 điểm y là cùng. Nếu bạn chỉ nhận được 1 điểm x và 1 điểm y thì ta viết 1 điểm P(x,y) thôi.

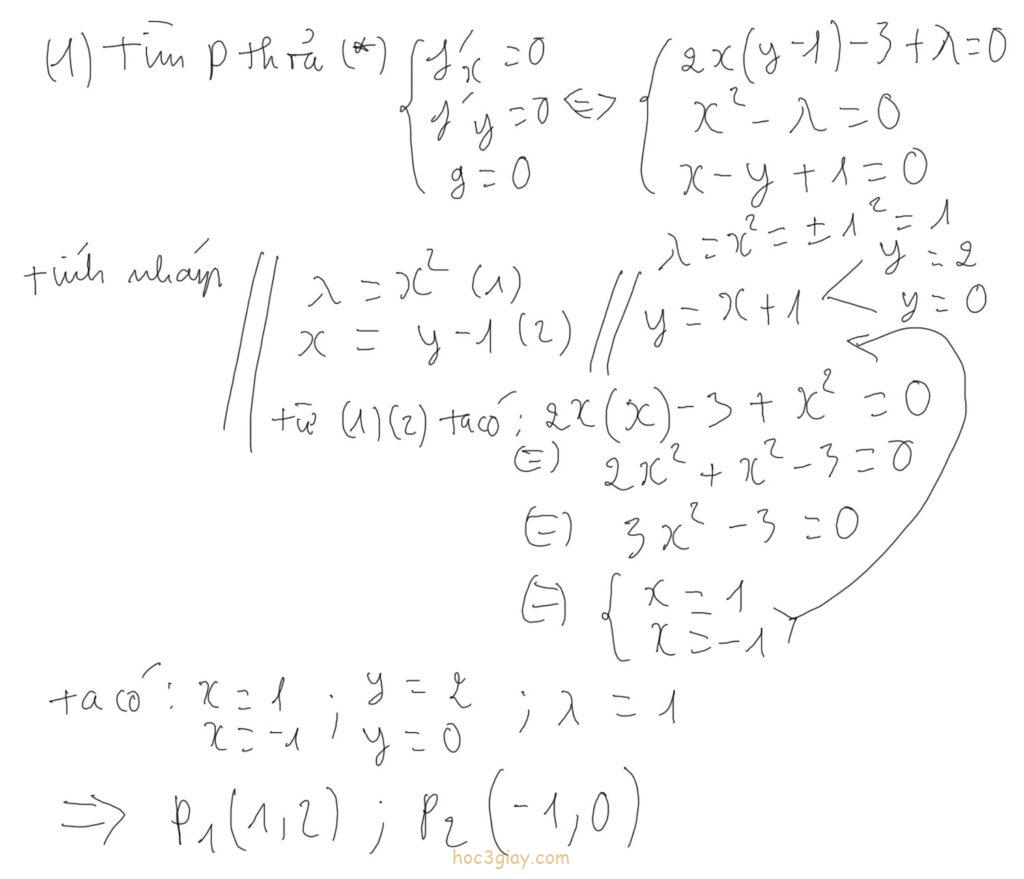
Bước 3: Xét d^2 L(x,y)=f”xxdx^2 + 2f”xydxdy + f”yydy^2 và kiểm tra 2 điều kiện nữa là dg(p)=0 (dg(p)=f’xdx + f’ydy), dx^2 + dy^2 ≠ 0 nếu điều kiện đúng thì ta tiếp tục, sai thì dừng. Cuối cùng ta thế các điểm trong P1, P2 đã tìm được ở bước 2 vào d^2 L(P1) và d^2 L(P2), nếu kết quả > 0 thì ta kết luận điểm P là điểm cực tiểu của f thỏa g=0 và ngược lại kết quả < 0 thì ta kết luận là điểm P là điểm cực đại của f thỏa g=0.

Lưu ý: Các đạo hàm riêng cấp 2 trong công thức d^2 L(x,y), ta sẽ trình bày nó ở bước 1 và hàm dg(p) cũng vậy ta trình bây nó ở chỗ bước đặt điều kiện ở bước 1.

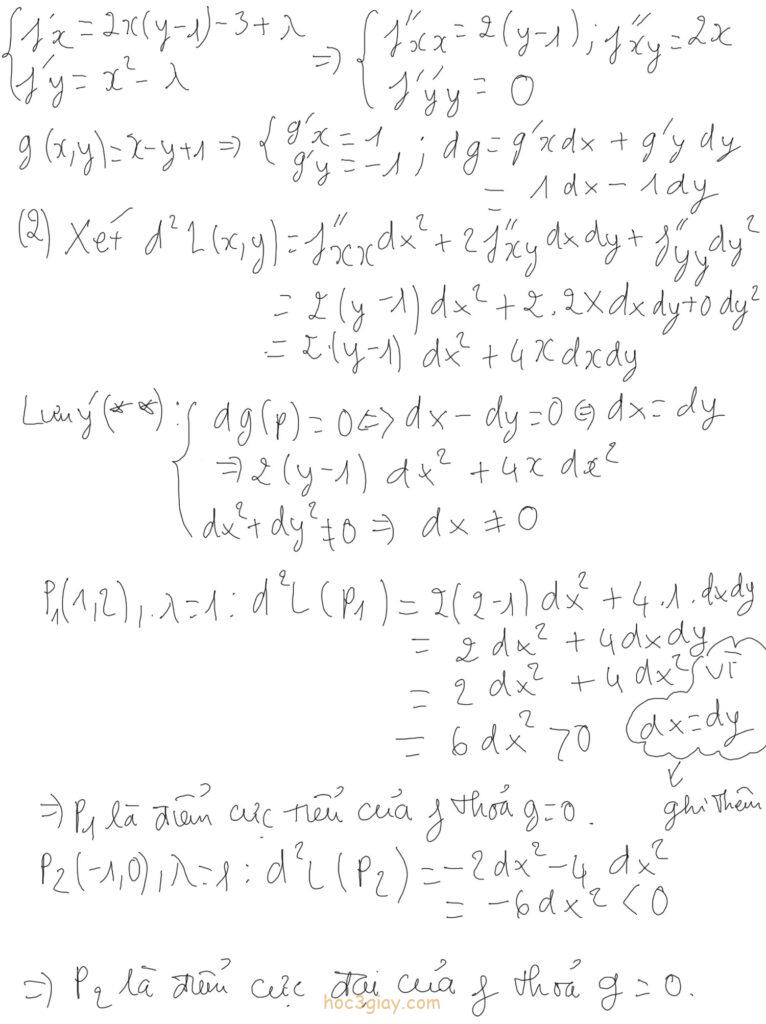
Lời kết

Chúc các bạn học tập vui vẻ và có được nhiều kinh nghiệm nhé. Hẹn gặp các bạn ở các bạn viết tiếp theo!