Cách Tìm Cực Trị Của Hàm Số Bậc 4 Hàm Trùng Phương (tìm Cực đại ...

Trang chủ » Cực Trị Của Hàm Số Bậc 4 Trùng Phương » Cách Tìm Cực Trị Của Hàm Số Bậc 4 Hàm Trùng Phương (tìm Cực đại ...

Có thể bạn quan tâm

Vậy cách tìm cực trị của hàm số bậc 4 hàm trùng phương (tìm cực đại, cực tiểu của hàm số bậc 4) như thế nào? Chúng ta hãy cùng tìm hiểu qua bài viết dưới đây. Đồng thời, qua bài viết này các em dễ dàng trả lời được các câu hỏi như: Hàm số bậc 4 có mấy cực trị? Hàm bậc 4 có 3 cực trị khi nào?...

° Cách tìm cực trị của hàm số bậc 4 hàm trùng phương (tìm cực đại, cực tiểu của hàm số bậc 4)

* Xét hàm số bậc bốn: y = f(x) = ax4 + bx2 + c (a≠0)

Cách 1:

- Bước 1: TXĐ: D = R

- Bước 2: Tính y' = 4ax3 + 2bx, cho y'=0 (hoặc y' không xác định)

- Bước 3: Lập bảng biến thiên

- Bước 4: Từ bảng biến thiên suy ra các điểm cực trị

Cách 2:

- Bước 1: Tìm tập xác định

- Bước 2: Tính f'(x), giải phương trình f'(x)=0 và ký hiệu xi (i=1;2;...) là nghiệm

- Bước 3: Tính f''(x) và f''(xi)

- Bước 4: Dựa vào dấu của f''(xi) suy ra tính chất cực trị của điểm xi.

* Ví dụ 1: Tìm điểm cực trị của hàm số bậc 3 sau: f(x) = x4 + 2x2 - 3

* Lời giải:

- TXĐ: D = R

- Ta có: y'= 4x3 + 4x = 4x(x2 + 1)

 y' = 0 ⇔ 4x(x2 + 1) = 0

 ⇔ x = 0 (do x2 + 1 > 0 với mọi x)

- Bảng biến thiên: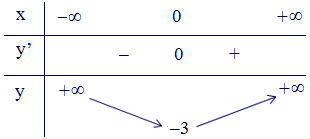Bảng biến thiên hàm số bậc 4 trùng phương Toán 12 tìm cực trị vd1

- Từ bảng biến thiên, ta thấy:

Hàm số đạt cực tiểu tại x = 0; yCT = -3. Hàm số không có điểm cực đại.

* Ví dụ 2: Tìm các điểm cực trị của hàm số bậc 4 trùng phương sau: y = x4 - 2x2 + 1 ;

* Lời giải:

- TXĐ: D = R.

- Ta cóL y' = 4x3 - 4x

 y' = 0 ⇔ 4x(x2 – 1) = 0

 ⇔ x = 0 hoặc x = -1 hoặc x = 1.

- Lại có: y" = 12x2 - 4, nên có:

 y"(0) = -4 < 0 ⇒ x = 0 là điểm cực đại của hàm số.

 y"(1) = 8 > 0 ⇒ x = 1 là điểm cực tiểu của hàm số.

 y"(-1) = 8 > 0 ⇒ x = -1 là điểm cực tiểu của hàm số.

Từ khóa » Cực Trị Của Hàm Số Bậc 4 Trùng Phương