Cách Tìm Đạo Hàm Sin2x. Bài Tập Vận Dụng Có Đáp Án - Marathon

Warning: mysqli_query(): (HY000/1): Can't create/write to file '/tmp/#sql-temptable-b851-2fa5ea-27cb.MAI' (Errcode: 28 "No space left on device") in /opt/bitnami/wordpress/wp-includes/wp-db.php on line 2162

Đạo hàm sin2x là phần kiến thức về đạo hàm lượng giác thường gặp trong kiến thức đạo hàm chương trình Đại số Toán trung học phổ thông. Dạng bài tập này xuất hiện khá nhiều trong các đề kiểm tra, do đó để giúp các em biết được những cách tính đạo hàm sin2x đơn giản, dễ áp dụng, Marathon Education đã tổng hợp những lý thuyết này và chia sẻ đến các em trong bài viết bên dưới đây.

>>> Xem thêm: Đạo Hàm Là Gì? Các Công Thức Tính Đạo Hàm Thường Gặp

Đạo hàm của y = sinx

Để tính đạo hàm của hàm số y = sinx, ta tiến hành áp dụng công thức đạo hàm lượng giác cơ bản sau:

(sinx)’ = cosx

Cách tìm đạo hàm sin2x 

Cách tính đạo hàm sin2x không quá khó. Cụ thể, các em có thể chọn một trong 2 cách cụ thể được nêu bên dưới đây để áp dụng giải các bài tập liên quan đến phần kiến thức này.

Tìm đạo hàm của hàm số y = sin2x

• Cách 1: Áp dụng đạo hàm lượng giác theo hàm số u

Từ đó, các em sẽ có:

(sin2x)’ = (2x)’.cos2x = 2.cos2x

• Cách 2: Áp dụng đạo hàm một tích (u.v)’ = (u)’.v + (v)’.u

Từ đó, các em sẽ có:

(sin2x)’ = 2(sinx.cosx)’

= 2[(sinx)’.cosx + sinx.(cosx)’]

= 2(cos2x – sin2x) = 2.cos2x.

Vậy đạo hàm của hàm số y = sin2x là 2cos2x

>>> Xem thêm: Cách Tìm Đạo Hàm Cos2x Và Bài Tập Vận Dụng Có Đáp Án

Cách tính đạo hàm của hàm số y = sin2x

Tính đạo hàm của hàm số y = sin2x

Phương Trình Lượng Giác Thường Gặp - Lý Thuyết Toán 11

y’ = (sin2x)’ = 2sinx.(sinx)’ = 2sinx.cosx = sin2x

Vậy đạo hàm của hàm số y = sin2x là sin2x

>>> Xem thêm: Dạng Bài Tập Và Cách Giải Bất Phương Trình Toán Lớp 10

Đạo hàm của các hàm số lượng giác

Một số công thức đạo hàm cơ bản của các hàm số lượng giác:

\begin{aligned} &\bull \text{Hàm số y = sinx có đạo hàm }\forall x\in\R \text{ và }(sinx)'=cosx.\\ &\bull \text{Hàm số y = cosx có đạo hàm }\forall x\in\R \text{ và }(cosx)'=-sinx.\\ &\bull \text{Hàm số y = tanx có đạo hàm }\forall x\not=\frac{\pi}{2}+k\pi,\ k\in \R \text{ và }(tanx)'=\frac{1}{cos^2x}.\\ &\bull \text{Hàm số y = cotx có đạo hàm }\forall x\not=k\pi,\ k\in \R \text{ và }(cotx)'=-\frac{1}{sin^2x}.\\ \end{aligned}

ĐĂNG KÝ NGAY

Bảng tổng hợp đạo hàm của hàm số lượng giác cơ bản và hàm số lượng giác ngược

Đạo hàm của hàm số lượng giác là phần kiến thức cơ bản. Dưới đây là bảng đạo hàm cho các hàm số lượng giác cơ bản và hàm số lượng giác ngược thường gặp. Cụ thể như sau:

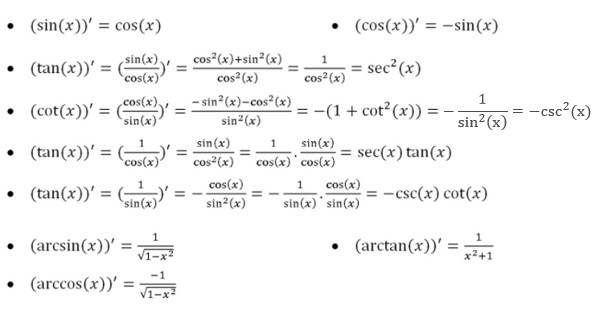
>>> Xem thêm: Tổng Hợp Các Kí Hiệu Trong Toán Học Phổ Biến Đầy Đủ Và Chi Tiết

Bài tập vận dụng tính đạo hàm của sin2x

Quá trình học lý thuyết luôn cần phải đi đôi với thực hành. Có như vậy, các em mới có thể dễ dàng hiểu bài và ghi nhớ các công thức một cách tốt hơn. Để giúp các em “thuộc nằm lòng” công thức tính đạo hàm sin2x, các em hãy cùng Marathon Education thực hành một số bài tập vận dụng như bên dưới đây. 

Lý Thuyết Bất Đẳng Thức Tam Giác: Quan Hệ Giữa 3 Cạnh Trong 1 Tam Giác

Ví dụ 1: Tính đạo hàm của hàm số

f(x)=sin2x-cos^23x

Lời giải:

f'(x)=(sin2x-cos^23x)'=2cos2x+3sin3x.2cos3x=2cos2x+3sin6x

Ví dụ 2: Tính đạo hàm của hàm số:

y=\frac{sin2x+cos2x}{2sin2x-cos2x}

Lời giải:

\begin{aligned} y'&=\left(\frac{sin2x+cos2x}{2sin2x-cos2x}\right)'\\ &=\frac{(sin2x+cos2x)'.(2sin2x-cos2x)-(2sin2x-cos2x)'.(sin2x+cos2x)}{(2sin2x-cos2x)^2}\\ &=\frac{(2cos2x – 2sin2x)(2sin2x – cos2x) – (4cos2x + 2sin2x)(sin2x + cos2x)}{(2sin2x-cos2x)^2}\\ &=\frac{–6cos^22x – 6sin^22x}{(2sin2x-cos2x)^2} = \frac{-6}{(2sin2x-cos2x)^2} \end{aligned}

Tham khảo ngay các khoá học online của Marathon Education

Gia sư Online Học Online Toán 12 Học Online Hóa 10 Học Online Toán 11 Học Online Toán 6 Học Online Toán 10 Học Online Toán 7 Học Online Lý 10 Học Online Lý 9 Học Online Toán 8 Học Online Toán 9 Học Tiếng Anh 6 Học Tiếng Anh 7

Trên đây là lý thuyết về đạo hàm lượng giác cũng như công thức và bài tập tính đạo hàm sin2x. Hy vọng sau khi đọc xong bài viết, các em có thể nắm được nhiều thông tin bổ ích để áp dụng vào quá trình học tập của mình.

Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học trực tuyến nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!