Cách Tìm điều Kiện để Biểu Thức Căn Thức Có Nghĩa (xác định) Và Bài ...
Có thể bạn quan tâm
Nắm vững cách tìm điều kiện xác định sẽ giúp bạn tránh được các lỗi sai cơ bản và làm nền tảng cho việc giải quyết các bài toán phức tạp hơn trong các kì thi quan trọng, đặc biệt là kì thi tuyển sinh vào lớp 10.
I. Cách tìm điều kiện để biểu thức căn thức có nghĩa
1. Phương pháp chung
• 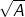 có nghĩa
có nghĩa 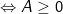
• 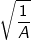 có nghĩa
có nghĩa 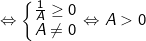
(vì biểu thức trong căn phải ≥ 0 và mẫu thức phải khác 0).
• 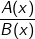 có nghĩa khi
có nghĩa khi 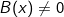
• 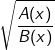 có nghĩa khi
có nghĩa khi 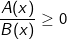 và
và 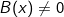
2. Lưu ý quan trọng
-
Nếu biểu thức chứa căn ở dưới mẫu, điều kiện của biểu thức trong căn phải là số dương (lớn hơn 0), không được bằng 0.
-
Nếu bài toán yêu cầu tìm tập xác định (TXĐ), sau khi tìm được điều kiện của x, bạn cần biểu diễn kết quả dưới dạng tập hợp. Ví dụ: x≥2 sẽ được viết là D=[2;+∞).
II. Bài tập Vận dụng: Tìm điều kiện xác định của căn thức
Bài tập 1: Tìm điều kiện của x để căn thức sau có nghĩa
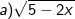
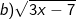
Lời giải:
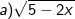
- Biểu thức này chỉ chứa căn bậc hai, nên biểu thức căn thức có nghĩa thì: 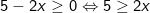
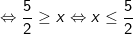
Kết luận: Để căn thức có nghĩa thì x ≤ 5/2.
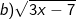
- Biểu thức này chỉ chứa căn bậc hai, nên biểu thức căn thức có nghĩa thì:
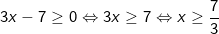
Kết luận: Để căn thức có nghĩa thì x ≥ 7/3.
Bài tập 2: Tìm điều kiện của x để biểu thức sau có nghĩa
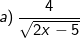

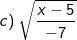
Lời giải:
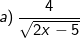
- Biểu thức này chứa căn bậc hai và đồng thời có phân thức ở mẫu, vì vậy để biểu thức có nghĩa thì:
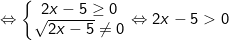
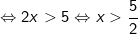
Kết luận: Để biểu thức có nghĩa thì x > 5/2.

- Biểu thức này chứa căn bậc hai và đồng thời có phân thức ở mẫu, vì vậy để biểu thức có nghĩa thì:
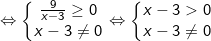
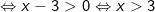
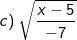
- Biểu thức này chứa căn bậc hai và mẫu thức đã là số khác 0 nên điều kiện để biểu thức có nghĩa là:
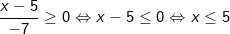
Bài tập 3: Tìm điều kiện của x để biểu thức sau có nghĩa
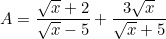
Lời giải:
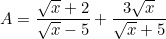
Để biểu thức có nghĩa thì căn thức có nghĩa và phân thức có nghĩa, tức là các biểu thức trong căn bậc hai phải ≥ 0 và mẫu thức các phân tức phải ≠0. Nên ta có:
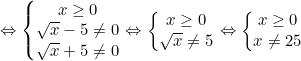
Kết luận: Biểu thức có nghĩa khi x ≥ 0 và x ≠ 25
Bài tập 4: Tìm điều kiện của x để biểu thức sau có nghĩa

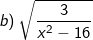
Lời giải:

- Để biểu thức căn thức có nghĩa thì: x2 - 6x + 5 ≥ 0
⇔ x2 - 5x - x + 5 ≥ 0 ⇔ x(x - 5) - (x - 5) ≥ 0
⇔ (x - 5)(x - 1) ≥ 0
⇔ [(x - 5) ≥ 0 và (x - 1) ≥ 0] hoặc [(x - 5) ≤ 0 và (x - 1) ≤ 0]
⇔ [x ≥ 5 và x ≥ 1] hoặc [x ≤ 5 và x ≤ 1]
⇔ [x ≥ 5] hoặc [x ≤ 1]
Kết luận: biểu thức có nghĩa khi x≤1 hoặc x≥5.
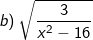
- Để biểu thức có nghĩa thì biểu thức trong căn bậc hai không âm (tức lớn hơn bằng 0) và mẫu thức khác 0. Nên ta có:
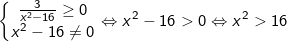
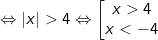
Kết luận: Biểu thức có nghĩa khi và chỉ khi x<-4 hoặc x>4.
Bài tập 5: Với giá trị nào của x thì biểu thức sau có nghĩa:
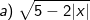
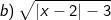
Lời giải:
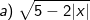
- Để biểu thức có nghĩa thì: 5 - 2|x| ≥ 0
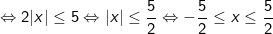
Vậy biểu thức có nghĩa khi và chỉ khi 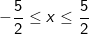
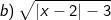
- Để biểu thức có nghĩa thì: |x - 2| - 3 ≥ 0
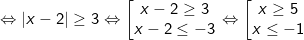
Vậy biểu thức có nghĩa khi và chỉ khi x≤-1 hoặc x≥5.
Bài tập 6: Với giá trị nào của x thì biểu thức sau có nghĩa:
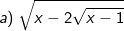
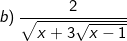
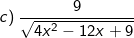
Bài tập 7: Với giá trị nào của x thì biểu thức sau có nghĩa:
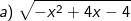
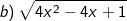
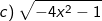
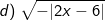
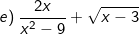
Từ khóa » Căn A Bình Có Nghĩa Khi Nào
-
Lý Thuyết Về Căn Thức Bậc Hai Và Hằng đẳng Thức √A^2
-
Tìm điều Kiện để Căn A Có Nghĩa Cực Hay, Có đáp án - Toán Lớp 9
-
Tìm điều Kiện để Biểu Thức Căn Có Nghĩa - Lớp 9
-
Căn Bậc Hai Và Hẳng đẳng Thức \(\sqrt{A^2}=A\)
-
Căn Thức Bậc Hai - Lý Thuyết Toán 9
-
Căn Bậc Hai – Wikipedia Tiếng Việt
-
Căn Thức Bậc Hai Và Hằng đẳng Thức √A2=|A| (căn A Bình Phương ...
-
1. Căn Thức Bậc Hai - SureTEST
-
Tìm điều Kiện để Biểu Thức Căn Có Nghĩa
-
Toán 9 - Căn Thức Bậc Hai Và Hằng đẳng Thức - Blog Lớp Học Tích Cực
-
Giải Toán 9 Bài 2. Căn Thức Bậc Hai Và Hằng đẳng Thức - Giải Bài Tập
-
Tập 1, Bài 6. Với Giá Trị Nào Của A Thì Mỗi Căn Thức Sau Có Nghĩa
-
Cách Tìm điều Kiện Có Nghĩa Của Căn Bậc 2 | Toán Học Lớp 6 7 8 9
-
Tìm X để Căn Thức Có Nghĩa Căn(1+x^2) - Hoa Lan