Cách Tìm đường Tiệm Cận đứng, Tiệm Cần Ngang Và Tiệm Cận Xiên ...
Có thể bạn quan tâm
Vậy cách tìm đường tiệm cận đứng, tiện cận ngang và tiệm cận xiên là gì? Cách tìm đường tiệm cận đứng, ngang và xiên như thế nào? chúng ta hãy cùng tìm hiểu qua bài viết này.
• Bài tập áp dụng tìm tiệm cận đứng, tiệm cận ngang của đồ thị hàm số
1. Đường tiệm cận ngang
Tiện cận ngang là gì?
a) Định nghĩa:
- Đường thẳng y = b được gọi là tiệm cận ngang của đồ thị hàm số y = f(x) nếu thỏa mãn một trong các điều kiện sau:
hoặc:
b) Chú ý:
- Điều kiện để đồ thị hàm số có tiệm cận ngang là bậc của đa thức P(x) bé hơn hoặc bằng bậc của đa thức Q(x).
* Ví dụ: Tìm tiệm cận ngang của đồ thị hàm số sau:
> Lời giải:
- TXĐ: D = R\{-3/2}
- Ta có:
Vây đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số
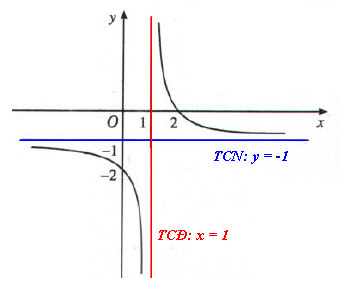
2. Đường tiệm cận đứng
Đường tiệm cận đứng là gì?
a) Định nghĩa:
- Đường thẳng x = a là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu thỏa một trong các điều kiện sau:
hoặc:
hoặc:
hoặc:
b) Chú ý:
- Đường thẳng x = a là đường tiệm cận đứng của đồ thị y = f(x) thì không thuộc tập xác định của f(x).
- Đối với hàm phân thức thì a là nghiệm Q(x) = 0.
* Ví dụ: Tìm tiệm cận ngang của đồ thị hàm số sau:
> Lời giải:
- TXĐ: D = R\{-3/2}
- Ta có:
Vậy đường thẳng x = -2 là tiemj cận đứng của đồ thị hàm số
3. Tiệm cận xiên (đọc thêm)
Tiệm cận xiên là gì?
a) Định nghĩa:
- Đường thẳng y = ax + b với a ≠ 0, được gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu thỏa một trong các điều kiện sau:
hoặc:
b) Cách xác định hệ số a, b của tiệm cận xiên
- Để xác định các hệ số a, b trong phương trình của đường tiệm cận xiên ta có thể áp dụng các công thức sau:
hoặc:
* Ví dụ: Tìm tiệm cận của đồ thị hàm số
> Lời giải:
- Hàm số đã cho xác định liên tục trên (−∞;1]U[1;+∞)
Ta có:
Vậy suy ra: y = 2x là tiệm cận xiên của đồ thị hàm số khí x → +∞.
Vậy suy ra: y = 2x là tiệm cận ngang của đồ thị hàm số khí x → -∞.
Từ khóa » Tiệm Cận Xiên Hàm Tham Số
-
Tiệm Cận Xiên Là Gì ? Tiệm Cận Xiên Của Hàm Tham Số Và đồ Thị Hàm ...
-
Phương Pháp Tìm đường Tiệm Cận Xiên Của đồ Thị Hàm Số - Các Bài ...
-
Tìm Tiệm Cận đồ Thị Hàm Số - Theza2
-
Tiệm Cận Xiên Của Hàm Số: Khái Niệm Và Phương Pháp Tìm - VOH
-
Khảo Sát đường Cong Tham Số | Maths 4 Physics & More...
-
3 Đường Tiệm Cận đứng, Ngang Và Xiên
-
Tiệm Cận Xiên Là Gì ? Tiệm Cận Xiên Của Hàm Tham Số Và đồ Thị Hàm ...
-
Đường Tiệm Cận Của đồ Thị Hàm Số: Tiệm Cận đứng, Ngang, Xiên
-
Tiệm Cận Xiên Là Gì? Tiệm Cận Xiêm Của đồ Thị Hàm Số Là Gì?
-
Tiệm Cận Xiên Là Gì ? Tiệm Cận Xiên Của Hàm Tham Số Và ... - TIP HAY
-
Cách Tìm Tiệm Cận Xiên Của Hàm Số, 3 Đường ...
-
[PDF] Qui Tắc Lôpital. 3 – Khảo Sát, Vẽ đồ Thị Hàm Số.
-
Phương Trình đường Tiệm Cận Xiên Của đồ Thị Hàm Số (y = F( X ) =