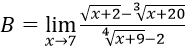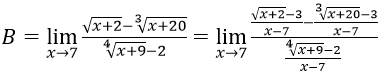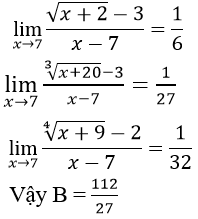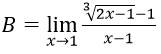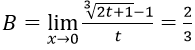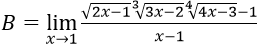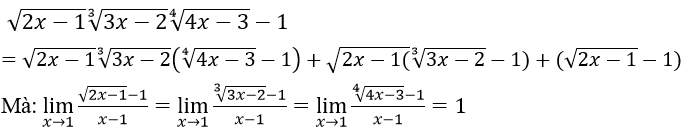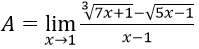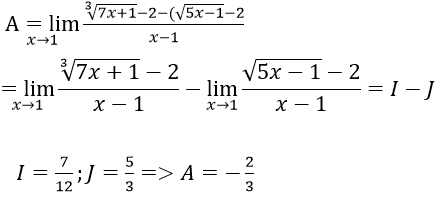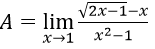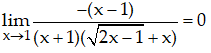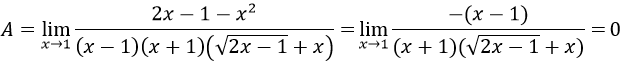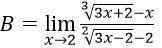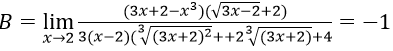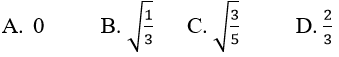Cách Tìm Giới Hạn Hàm Số Dạng 0/0, Dạng Vô ...
Có thể bạn quan tâm
Cách tìm giới hạn hàm số dạng 0/0, dạng vô cùng trên vô cùng cực hay
A. Phương pháp giải & Ví dụ
Tìm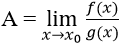 
trong đó f(x0) = g(x0) = 0
Dạng này ta gọi là dạng vô định 0/0
Để khử dạng vô định này ta sử dụng định lí Bơzu cho đa thức:
Định lí: Nếu đa thức f(x) có nghiệm x = x0 thì ta có :f(x) = (x-x0)f1(x)
* Nếu f(x) và g(x) là các đa thức thì ta phân tích
f(x) = (x-x0)f1(x)và : g(x) = (x-x0)g1(x).
Khi đó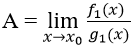 
, nếu giới hạn này có dạng 0/0 thì ta tiếp tục quá trình như trên.
Ví dụ minh họa
Bài 1: 
Hướng dẫn:
Ta có:
Mà
Bài 2: 
Hướng dẫn:
Đặt t = x - 1 ta có:
Bài 3: 
Hướng dẫn:
Ta có:
Nên ta có B = 1 + 1 + 1 = 3
Bài 4: 
Hướng dẫn:
Ta có:
Vậy A = -2/3
Bài 5: Tìm các giới hạn sau: 
Hướng dẫn:
Ta có: 
Bài 6: Tìm giới hạn sau: 
Hướng dẫn:
Ta có:
B. Bài tập vận dụng
Bài 1: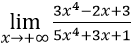 
bằng:
A. 0 B. 4/9 C. 3/5 D. +∞
Bài 2: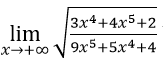 
bằng:
Bài 3: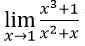 
bằng:
A. -3
B. -1
C. 0
D. 1
Bài 4: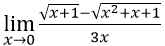 
bằng:
A. 0 B. -1/6 C. -1/2 D. -∞
Bài 5: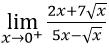 
bằng:
A. +∞ B. 2/5 C. -7 D. -∞
Bài 6: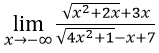 
bằng:
A. 2/3 B. 1/2 C. -2/3 D. -1/2
Bài 7: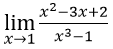 
bằng:
A. -2/3 B. -1/3 C. 0 D. 1/3
Bài 8: 
bằng:
A. +∞
B. 4
C. 0
D. -∞
Bài 9: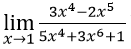 
bằng số nào sau đây?
Bài 10: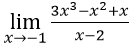 
bằng
A. 5 B. 1 C. 5/3 D. -5/3
Bài 11: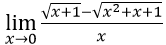 
bằng:
A. 0 B. -1 C. -1/2 D. -∞
Bài 12: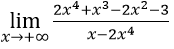 
bằng:
A. -2
B. -1
C. 1
D. 2
Bài 13: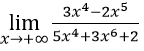 
bằng:
A. -∞ B. 3/5 C. -2/5 D. 0
Bài 14: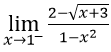 
bằng:
A. 1/4 B. 1/6 C. 1/8 D. -1/8
Bài 15: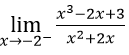 
bằng:
A. +∞ B. 1/8 C. -9/8 D. -∞
Từ khóa » Giới Hạn Hàm Số Dạng 0/0 Nâng Cao
-
Giới Hạn Của Hàm Số Dạng Vô định 0/0
-
Cách Tìm Giới Hạn Hàm Số Dạng 0/0, Dạng Vô Cùng ...
-
Cách Tìm Giới Hạn Hàm Số Dạng 0/0, Dạng Vô Cùng Trên ... - Haylamdo
-
Giới Hạn Hàm Số (Dạng 0/0) _Toán 11_ Thầy Nguyễn Quốc Chí
-
19 BÀI GIỚI HẠN HÀM SỐ DẠNG 0/0 RẤT CƠ BẢN - Tài Liệu - 123doc
-
Tìm Giới Hạn Hàm Số Dạng 0/0, Dạng Vô Cùng Trên Vô Cùng - Toán Lớp ...
-
Tìm Giới Hạn Hàm Số Dạng 0 Nhân Vô Cùng - Toán Lớp 11
-
Lim Dạng 0 0 Nâng Cao - Giới Hạn Hàm Số Dạng Không Trên Không
-
Giới Hạn Hàm Số - Cách Xử Lý Các Dạng Vô định
-
Cách Tìm Giới Hạn Hàm Số Dạng 0/0, Dạng Vô ...
-
Giới Hạn Hàm Số Dạng 0/0
-
Giới Hạn Hàm Số Dạng Không Trên Không - 0/0
-
Giới Hạn Hàm Số (Dạng 0/0) _Toán 11_ Thầy Nguyễn Quốc Chí
-
Một Số Dạng Cơ Bản Và Cách Giải Giới Hạn Dạng Vô định 0/0