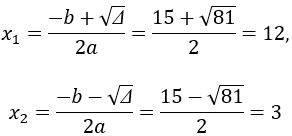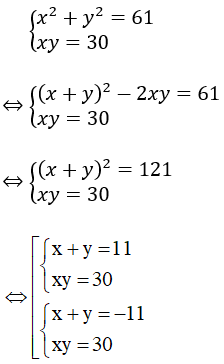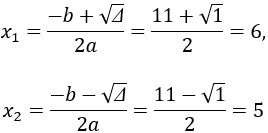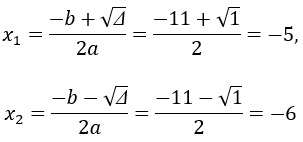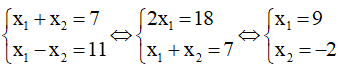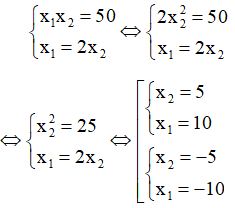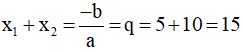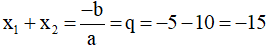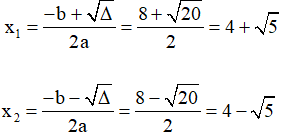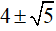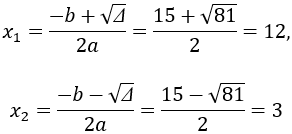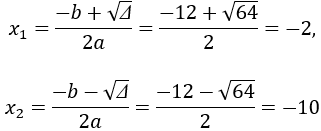Cách Tìm Hai Số Khi Biết Tổng Và Tích Của Chúng Cực Hay
Có thể bạn quan tâm
Cách tìm hai số khi biết tổng và tích của chúng cực hay
A. Phương pháp giải
- Bài toán: Tìm hai số u và v biết: u + v = S, u.v = P
- Cách giải:
+ Kiểm tra điều kiện để tồn tại hai số u và v: Nếu S2< 4P thì không tồn tại hai số u và v, nếu S2≥ 4P thì tồn tại hai số u và v
+ Trong trường hợp tồn tại, hai số cần tìm là nghiệm của phương trình
x2– Sx + P = 0
B. Bài tập
Câu 1: Tìm u – v biết u + v = 15, u.v = 36, u > v
Giải
Vì S = 15, P = 36 thỏa mãn S2≥ 4P nên tồn tại hai số u và v
Hai số đó là nghiệm của phương trình x2– 15x + 36 = 0
∆ = (-15)2– 4.36 = 225 – 144 = 81 > 0
Suy ra phương trình có 2 nghiệm phân biệt
Vậy hai số cần tìm là: 12 và 3
Do u > v nên u = 12 và v = 3 ⇒ u – v = 12 – 3 = 9
Câu 2: Tìm hai số x, y biết x2+ y2= 61 và xy = 30
Giải
Theo giả thiết ta có:
+ Xét TH1: x + y = 11 và xy = 30
Với S = 11, P = 30 thì S2= 121 > 4P = 120 nên tồn tại hai số x và y
Hai số x và y là nghiệm của phương trình x2- 11x + 30 = 0
∆ = (11)2– 4.30 = 121 – 120 = 1 > 0
Suy ra phương trình có 2 nghiệm phân biệt
Vậy hai số cần tìm là: x = 5, y = 6 hoặc x = 6, y = 5
+ Xét TH2: x + y = -11 và xy = 30
Với S = -11, P = 30 thì S2= 121 > 4P = 120 nên tồn tại hai số x và y
Hai số x và y là nghiệm của phương trình: x2+ 11x + 30 = 0
∆ = (-11)2– 4.30 = 121 – 120 = 1 > 0
Suy ra phương trình có 2 nghiệm phân biệt:
Vậy hai số cần tìm là: x = -5, y = -6 hoặc x = -6, y = -5
Kết hợp 2 trường hợp ta tìm được 4 cặp số x,y thỏa mãn đầu bài
x = 5, y = 6 hoặc x = 6, y = 5 hoặc x = -5, y = -6 hoặc x = -6, y = -5
Câu 3: Cho phương trình x2– 7x + q = 0, biết hiệu hai nghiệm bằng 11. Tìm q và hai nghiệm của phương trình
Giải
Theo Vi-et ta có: x1+ x2= 7 (1)
Mặt khác theo giả thiết hiệu 2 nghiệm bằng 11 nên: x1- x2= 11 (2)
Từ (1) và (2) ta có hệ:
Ta có: x1x2= q = 9.(-2) = -18
Vậy q = -18 và 2 nghiệm của phương trình là 9 và -2
Câu 4: Cho phương trình x2– qx + 50 = 0, biết phương trình có hai nghiệm và có một nghiệm gấp 2 lần nghiệm kia. Tìm q và hai nghiệm của phương trình
Giải
Theo Vi-et ta có: x1x2= 50 (1)
Mặt khác theo giả thiết,phương trình có một nghiệm gấp 2 lần nghiệm kia nên: x1= 2x2(2)
Từ (1) và (2) ta có hệ:
Với x1= 10, x2= 5 thì:
Với x1= -10, x2= -5 thì:

Câu 5: Tìm hai số biết
a. Tổng của chúng bằng 8, tích của chúng bằng 11
b. Tổng của chúng bằng 17, tích của chúng bằng 180
Giải
a. Vì S = 8, P = 11 thỏa mãn S2≥ 4P nên tồn tại hai số cần tìm
Hai số đó là nghiệm của phương trình x2– 8x + 11 = 0
∆ = (-8)2– 4.11 = 64 – 44 = 20 > 0
Suy ra phương trình có 2 nghiệm phân biệt
Vậy hai số cần tìm là:
b. Với S = 17, P = 180 thì S2= 289 < 4P = 720 nên không tồn tại hai số thỏa mãn yêu cầu của đề bài
Câu 6:Tìm hai số u và v biết
a. u + v = 15 và u.v = 36
b. u + v = 4 và u.v = 7
c. u + v = -12 và u.v = 20
Giải
a. Với S = 15, P = 36 thì S2= 225 > 4P = 144 nên tồn tại hai số u và v
Hai số u và v là nghiệm của phương trình: x2– 15x + 36 = 0
∆ = (-15)2– 4.36 = 225 – 144 = 81 > 0
Suy ra phương trình có 2 nghiệm phân biệt:
Vậy hai số cần tìm là: u = 12, v = 3 hoặc u = 3, v = 12
b. Với S = 4, P = 7 thì S2= 16 < 4P = 28 nên không tồn tại hai số u,v thỏa
mãn yêu cầu của đề bài
c. Với S = -12, P = 20 thì S2= 144 > 4P = 80 nên tồn tại hai số u và v
Hai số u và v là nghiệm của phương trình x2+ 12x + 20 = 0
∆ = (12)2– 4.20 = 144 – 80 = 64 > 0
Suy ra phương trình có 2 nghiệm phân biệt
Vậy hai số cần tìm là: u = -2, v = -10 hoặc u = -10, v = -2
Từ khóa » Giải Hệ Phương Trình Tích Và Tổng
-
Các Bài Toán Tìm 2 Số Khi Biết Tổng Và Tích. - Kiến Guru
-
Cách Tìm Hai Số Khi Biết Tổng Và Tích Của Chúng - Abcdonline
-
Cách Tìm Hai Số Khi Biết Tổng Và Tích Của Chúng Cực Hay - Toán Lớp 9
-
Cách Tìm Hai Số Khi Biết Tổng Và Tích Của Chúng Cực Hay | Toán Lớp 9
-
Dạng 5: Ứng Dụng định Lý Vi-et Tìm Hai Số Biết Tổng Và Tích Của Chúng
-
TOP 7 Trang Web Giải Hệ Phương Trình Online Miễn Phí, Chính Xác
-
Giải Hệ Phương Trình Bằng Cách đưa Về Dạng Tích - Tài Liệu - 123doc
-
Cách Tìm 2 Số Khi Biết Tổng Và Tích Của Chúng - Học Toán 123
-
KĨ NĂNG BIẾN ĐỔI HỆ PHƯƠNG TRÌNH VỀ DẠNG TÍCH
-
Giải Bài Toán Bằng Cách Lập Hệ Phương Trình Dạng Tìm Số
-
Cách Giải Phương Trình Bậc 2 Và Tính Nhẩm Nghiệm PT Bậc 2
-
Không Giải Phương Trình, Hãy Tính Tổng Và Tích Các Nghiệm (nếu Có)...
-
Hệ Thức Vi-ét Và ứng Dụng