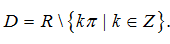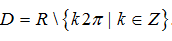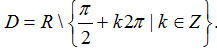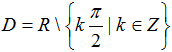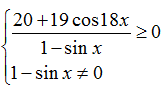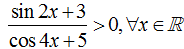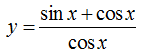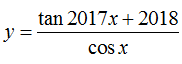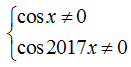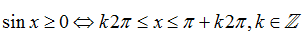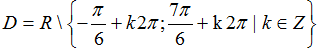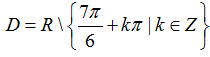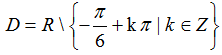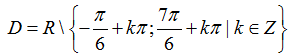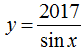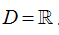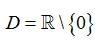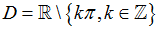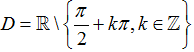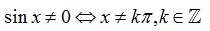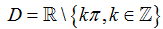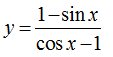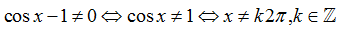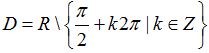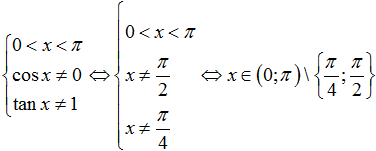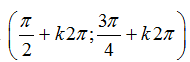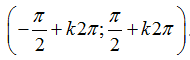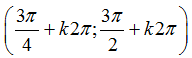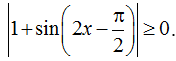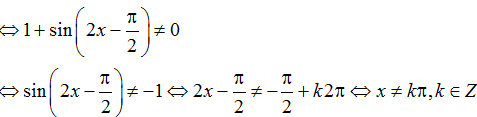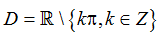Cách Tìm Tập Xác định Của Hàm Số Lượng Giác Cực Hay
Có thể bạn quan tâm
Cách tìm tập xác định của hàm số lượng giác cực hay
A. Phương pháp giải
+ Hàm số y = 1/f(x) xác định khi f(x) ≠ 0 .
+ Hàm số y= √(f(x)) xác định khi f(x) ≥ 0.
+ Hàm số y = 1/√(f(x)) xác định khi f(x)> 0
+ Hàm số y= tan [f(x)] xác định khi cos[f(x)] ≠ 0 .
+ Hàm số y = cot [f(x)] xác định khi sin[ f(x)] ≠ 0
+ Hàm số y= tan[ f(x)]+cot[g(x)] xác định khi cos[f(x)] ≠ 0;sin[ g(x)] ≠ 0
* Chú ý:
sinx ≠ 0 ⇔ x ≠ k.π
cosx ≠ 0 ⇔ x ≠ π/2+kπ với k nguyên
sinx ≠ 1 ⇔ x ≠ π/2+k2π và sinx ≠ -1 ⇔ x ≠ -π/2+k2π
cosx ≠ 1 ⇔ x ≠ k2π và cosx ≠ -1 ⇔ x ≠ π+k2π

B. Ví dụ minh họa
Ví dụ 1. Tập xác định của hàm số 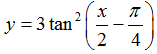
A. R
B.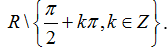
C.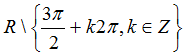
D.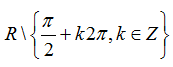
Lời giải:
Chọn C
Hàm số xác định khi cos(x/2-π/4) ≠ 0
⇔ x/2-π/4 ≠ π/2+kπ ⇔ x/2 ≠ 3π/4+kπ
⇔ x ≠ 3π/2+k2π,k ∈ Z
Ví dụ 2: Tìm tập xác định của hàm số 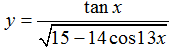
A.Ta có 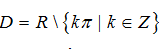
B .D =
C. Ta có 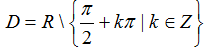
D.
Ta có 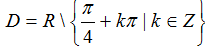
Lời giải:
Chọn C
Ta có 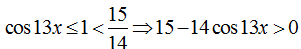
Vậy hàm số đã cho xác định khi 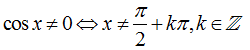
Ví dụ 3: Tìm tập xác định của hàm số: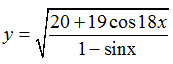
A.
B.
C.
D.
Lời giải:
Chọn C
Hàm số đã cho xác định khi
Mà cos18x ≥ -1 ⇒ 19cos18 x ≥ -19
⇒ 20+ 19cos18x ≥ 20-19= 1 > 0
Vậy 20+19cos18x > 0, ∀x ∈ R nên hàm số đã cho xác định khi và chỉ khi:
Vậy hàm số đã cho xác định khi x ≠ π/2+k2π,k ∈ Z
Ví dụ 4: Hàm số nào sau đây có tập xác định là R?
A.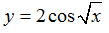
B.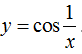
C.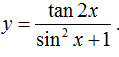
D.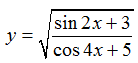
Lời giải:
Chọn D
Ta xét các phương án:
+ Với A thì hàm số xác định khi
+Với B thì hàm số xác định khi
+ Với C thì hàm số xác định khi tan2x xác định ≤ ⇒ cos2x ≠ 0
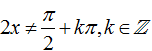
+ Với D thì cos 4x ≥ -1 và sin2x ≥ -1 với ∀ x
⇒ cos4x + 5 > 0 và sin2x + 3 > 0với mọi x
⇒
Ví dụ 5: Hàm số nào sau đây có tập xác định khác với các hàm số còn lại?
A. y= tanx
B.
C.
D.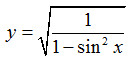
Lời giải:
Chọn C
Với A thì hàm số xác định khi cosx khác 0
Với B thì hàm số xác định khi cosx khác 0
Với C thì hàm số xác định khi
Từ đây ta chọn C do khác với A và B
Ví dụ 6: Hàm số 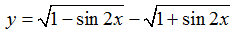
A.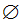
B.D=R .
C.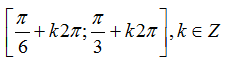
D.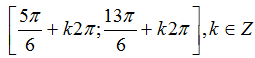
Lời giải:
Chọn B
Hàm số đã cho xác định khi:
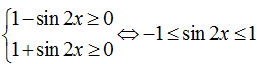
Do đó hàm số đã cho có tập xác định: D= R
Ví dụ 7: Chọn khẳng định đúng:
A. Hàm số 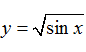
B. Hàm số 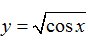
C. Hàm số 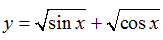
D. Hàm số 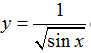
Lời giải:
Chọn C
Ta xét các phương án:
+ Với A thì hàm số 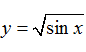
Vậy A sai.
+ Với B thì hàm số 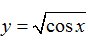
Vậy B sai.
+ Với C thì hàm số xác định khi 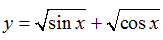
Vậy C đúng.
Ví dụ 8: Tập xác định của hàm số D.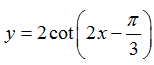
A. R\{π/6+kπ/2,k ∈ Z}.
B.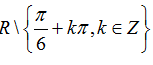
C.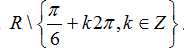
D.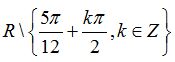
Lời giải:
Chọn A
Hàm số xác định khi sin(2x-π/3) ≠ 0
⇔2x-π/3 ≠ kπ ⇔ 2x ≠ π/3+ kπ
⇔ x ≠ π/6+kπ/2,k ∈ Z
Ví dụ 9. Xét hai mệnh đề sau:
(I): Các hàm số y= sin x và y= cosx có chung tập xác định là R
(II): Các hàm số y= tanx và y= cotx có chung tập xác định là
.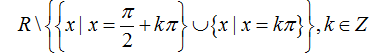
A. Chỉ (I) đúng. B. Chỉ (II) đúng. C. Cả hai đều sai. D. Cả hai đều đúng.
Lời giải:
Chọn A
+ Hai hàm số y= sinx và y= cosx có chung tập xác định là D = R
⇒ (I) đúng
+ Hàm số y= tanx tập xác định là 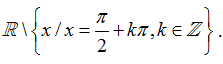
Và hàm số y= cot x tập xác định là 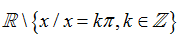
suy ra (II) sai
Ví dụ 10: Tập xác định của hàm số 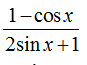
A.
B.
C.
D.
Lời giải:
Chọn A
ĐK: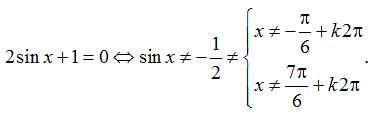
Tập xác định .
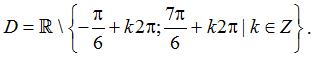
Ví dụ 11: Tập xác định của hàm số 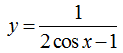
A.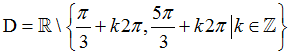
B.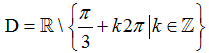
C.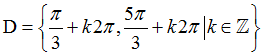
D.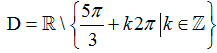
Lời giải:
Chọn A
Cách 1: Hàm số đã cho xác định khi 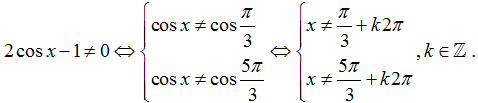
Cách 2: Sử dụng máy tính cầm tay tính giá trị của hàm số 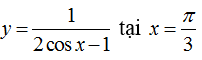
và 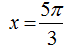
ta thấy hàm số đều không xác định, từ đây ta chọn A
Ví dụ 12: Tìm tập xác định D của hàm số 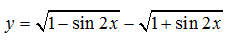
A.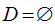
B=R
C.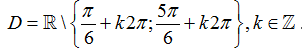
D.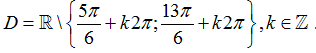
Lời giải:
Chọn B
Ta có 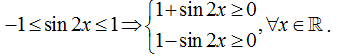
Vậy tập xác định D=R .
Ví dụ 13. Tìm tập xác định D của hàm số
A.
B.
C.
D.
Lời giải:
Chọn C.
Hàm số xác định khi và chỉ khi
Vậy tập xác định
Ví dụ 14. Tìm tập xác định D của hàm số
A.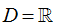
B.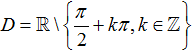
C.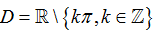
D.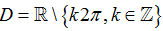
Lời giải:
Chọn D
Hàm số xác định khi và chỉ khi
Vậy tập xác định 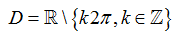
Ví dụ 15. Tập xác định của hàm số 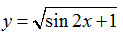
A.
B.
C.
D.
Lời giải:
Chọn B
Ta có 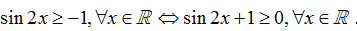
Vậy hàm số đã cho xác định với mọi x∈R
Ví dụ 16: Cho hàm số 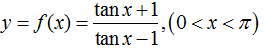
A.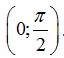
B.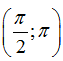
C.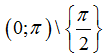
D.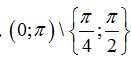
Lời giải:
Chọn D
Hàm số xác định khi
Ví dụ 17: Cho hàm số 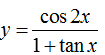
A.
B.
C.
D.
Lời giải:
Chọn B
Hàm số đã cho xác định khi 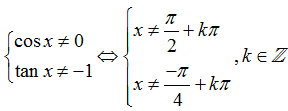
Khoảng 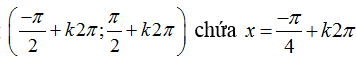
nên hàm số không xác định trong khoảng này
Ví dụ 18: Tập xác định của hàm số y= cosx/(cos3x.cos( x- π/3).cos( π/3+x) ) là:
A.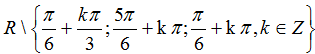
B.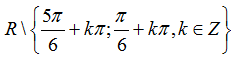
C.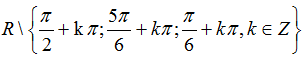
D.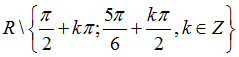
Lời giải:
Chọn A
Hàm số đã cho xác định khi và chỉ khi:
cos3x.cos( x- π/3).cos( π/3+x) ≠ 0
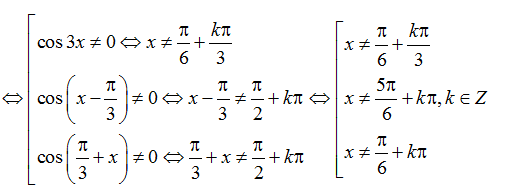
Ví dụ 19: Tập xác định của hàm số 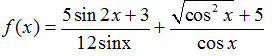
A.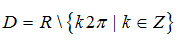
B.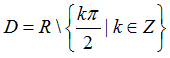
C.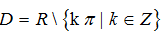
D.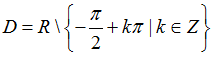
Lời giải:
Chọn B
Hàm số 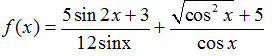
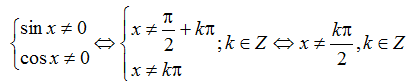
Vậy tập xác định của hàm số là: D=R\{kπ/2;k ∈ Z}.
Ví dụ 20: Tập xác định của hàm số 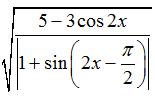
A.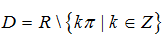
B.D=R.
C.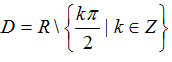
D.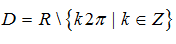
Lời giải:
Chọn A
Ta có -1 ≤ cos2x ≤ 1 nên -3 ≤ -3cos2x ≤ 3
⇒ 2 ≤ 5-3cos2x ≤ 8. Vậy 5-3cos2x > 0 với mọi x. .
Mặt khác
Hàm số đã cho xác định
Tập xác định
Ví dụ 21. Hàm số 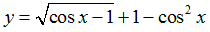
A.x ≠ π/2 +kπ, k∈Z .
B.x=0 .
C.x≠ kπ,k∈Z .
D.x= k2π,k∈Z .
Lời giải:
Chọn D
Hàm số đã cho xác định khi cos x - 1 ≥0, mà cos x - 1 ≤0,∀x∈R
Do vậy để hàm số xác định thì cosx=1, x= k2π,k∈Z
Ví dụ 22: Xét hai mệnh đề:
(I): Các hàm số y= 1/sinx và y= cotx có chung tập xác định là 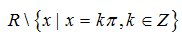
(II):Các hàm số y= 1/cosx và y= tanx có chung tập xác định là 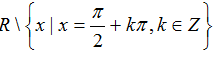
A. Chỉ (I) đúng.
B. Chỉ (II) đúng.
C. Cả hai đều sai.
D.Cả hai đều đúng.
Lời giải:
Chọn D
+ Ta thấy cả hai hàm số y= 1/sinx và y = cot x đều xác định khi sinx ≠ 0 .
+ Tương tự thì hai hàm số ở mệnh đề II đều xác định khi cosx ≠ 0 .
⇒ Cả hai mệnh đề đã cho là đúng .
Ví dụ 23: Cho hàm số 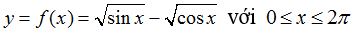
A.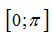
B.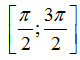
C.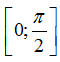
D.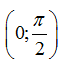
Lời giải:
Chọn C
Hàm số xác định khi và chỉ khi: 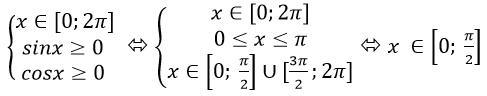
C. Bài tập vận dụng
Câu 1:Tìm tập xác định D của hàm số y=1/(sinx-cosx)
A. D=R .
B. D= R\{(-π)/4+k2π; k ∈ Z}.
C. D= R\{π/4+k2π; k ∈ Z}.
D. D= R\{π/4+kπ; k ∈ Z}
Câu 2:Tìm tập xác định D của hàm số y= cot(2x- π/4)+sin2x.
A. R\{π/4+kπ; k ∈ Z}.
B. D= R
C. R\{π/8+kπ; k ∈ Z}.
D. Đáp án khác
Câu 3:Tìm tập xác định D của hàm số y= √(sinx+2)
A.D=R .
B.D=[-2;+∞] .
C.D=[0;2π] .
D.D=Ø .
Câu 4:Tìm tập xác định D của hàm số y= √(sinx-2) .
A. D=R .
B. D=R\{kπ;k ∈ Z} .
C. D=[-1;1] .
D. D=Ø .
Câu 5:Xét bốn mệnh đề sau
(1) Hàm số y= sinx có tập xác định là R
(2) Hàm số y= cosx có tập xác định là R
(3) Hàm số y= tan x có tập xác định là R\{kπ|k ∈ Z}
(4) Hàm số y= cotx có tập xác định là R\{kπ/2|k ∈ Z}
Số mệnh đề đúng là
A. 1. B. 2. C. 3. D. 4.
Câu 6:Tập xác định của hàm số y=(1-sinx)/(sinx+1) là
A.x ≠ π/2+k2π .
B.x ≠ k2π .
C.x ≠ 3π/2+k2π .
D.x ≠ π+k2π .
Câu 7:Tập xác định của hàm số y=(1-3cosx)/sinx là
A.x ≠ π/2+kπ .
B.x ≠ k2π .
C.x ≠ kπ/2 .
D.x ≠ kπ .
Câu 8:Tập xác định của hàm số y=tan(2x-π/3) là
A.x ≠ π/6+kπ/2 .
B.x ≠ 5π/12+kπ .
C.x ≠ π/2+kπ .
D.x ≠ 5π/12+kπ/2 .
Câu 9:Tìm tập xác định của hàm số y=sin(1/x)+2x
A. D=[-2;2]
B. D=[-1;1]\{0}
C. D=R
D. D=R\{0}
Câu 10:Tìm tập xác định của hàm số y=(1+cosx)/sinx
A. D=R\{kπ|k ∈ Z} .
B. D=R\{π/2+kπ|k ∈ Z}.
C. D=R\{π+k2π|k ∈ Z} .
D. D=R\{k2π|k ∈ Z} .
Câu 11:Tập xác định của hàm số y= tan(2x+π/3) là
A. D. D=R\{π/2+kπ|k ∈ Z} .
B. D. D=R\{π/6+kπ|k ∈ Z} .
C. D. D=R\{π/12+kπ|k ∈ Z} .
D. D. D=R\{π/12+kπ/2|k ∈ Z} .
Câu 12:Tìm tập xác định D của hàm số y=1/(sin(x-π/2))
A. D= R\{k π/2;k ∈ Z}.
B. D=R {kπ;k ∈ Z}.
C. D= R\{(1+2k) π/2;k ∈ Z}.
D. D=R {(1+2k)π;k ∈ Z}.
Câu 13:Tập xác định của hàm số y= sinx/(sinx+cosx)
A.D=R\{-π/4+kπ;k ∈ Z}
B.D=R\{kπ/4;k ∈ Z}
C.D=R\{π/4+kπ,π/2+kπ;k ∈ Z}
D.D=R\{π/4+kπ;k ∈ Z}
Câu 14:Tập xác định của hàm số y= tanx/(cosx-1)
A.x≠ k2π
B.x=π/3+k2π
C.x≠ π/2+kπ và x≠ k2π
D.x≠ π/2+kπ và x≠ π/3+kπ
Câu 15:Tìm tập xác định D của hàm số y=1/ √(1-sinx) .
A.D=R\{kπ;k ∈ Z}
B.D=R\{π/2+kπ;k ∈ Z}
C.D=R\{π/2+k2π;k ∈ Z}
D.D=∅
Câu 16:Tập xác định của hàm số
A.D=R\{-π/6+k2π;k ∈ Z} .
B.D=R\{7π/6+kπ,k2π;k ∈ Z} .
C.D=R\{k2π;k ∈ Z} .
D. Đáp án khác
Câu 17:Tập xác định của hàm số 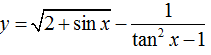
A.D=R\{±π/4+kπ,π/2+kπ;k ∈ Z} .
B.D=R\{kπ/2;k ∈ Z} .
C.D=R\{π/4+kπ;k ∈ Z} .
D.D=R\{±π/4+kπ;k ∈ Z} .
Câu 18: Hàm số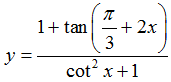
A.D=R\{π/6+kπ/2,kπ;k ∈ Z} .
B.D=R\{π/12+kπ,kπ/2;k ∈ Z} .
C.D=R\{π/12+kπ,kπ;k ∈ Z} .
D.D=R\{π/12+kπ/2,kπ;k ∈ Z} .
Câu 19:Tập xác định của hàm số y=cotx/(sinx-1) là:
A.D=R\{π/3+k2π;k ∈ Z} .
B.D=R\{kπ/2;k ∈ Z} .
C.D=R\{π/2+k2π,kπ;k ∈ Z} .
D.D=R\{π/2+k2π;k ∈ Z} .
Câu 20:Tập xác định của hàm số y=2016tan20172x là
A.D=R\{π/2+kπ;k ∈ Z}
B.D=R\{kπ/2;k ∈ Z}
C.D=R
D.D=R\{π/4+kπ/2;k ∈ Z}
Câu 21:Tập xác định của hàm số 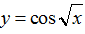
A. D=[0;2π]
B. D=[0;+∞]
C. D=R
D. D=R\{0}
Câu 22:Tập xác định của hàm số y=(2sinx+1)/(1-cosx) là:
A. x ≠ kπ/2 .
B. x ≠ kπ .
C. x ≠ π/2+kπ .
D. x ≠ π/2+k2π .
Câu 23: Tập xác định của hàm số y= tan 2x là
A. x ≠ -π/4+kπ/2 .
B. x ≠ π/2+kπ .
C. x ≠ π/4+kπ/2 .
D. x ≠ π/4+kπ .
Câu 24:Để tìm tập xác định của hàm số y= tanx+ cosx, một học sinh đã giải theo các bước sau:
Bước 1: Điều kiện để hàm số có nghĩa là sinx≠ 0 và cosx≠ 0 .
Bước 2: ⇒ x≠ π/2+kπ và x≠ kπ ;k ∈ Z
Bước 3: Vậy tập xác định của hàm số đã cho là D=R\{π/2+kπ,kπ;k ∈ Z} .
Bài giải của bạn đó đúng chưa? Nếu sai, thì sai bắt đầu ở bước nào?
A. Bài giải đúng.
B. Sai từ bước 1.
C. Sai từ bước 2.
D. Sai từ bước 3.
Câu 25:Tập xác định D của hàm số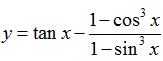
A.D=R\{π/2+k2π;k ∈ Z}
B.D=R\{π/2+kπ;k ∈ Z}
C.D=R\{π/2+kπ/2;k ∈ Z}
D.D=R\{kπ/2;k ∈ Z}
Câu 26:Tìm tập xác định của hàm số y=1/(sin2x-cos2x)
A.D=R\{π/2+kπ;k ∈ Z}
B.D=R\{kπ/2;k ∈ Z}
C.D=R
D.D=R\{π/4+kπ/2;k ∈ Z}
Câu 27:Tìm tập xác định của hàm số y=2017tan2x/sin2x-cos2x
A.D=R\{π/2+kπ;k ∈ Z}
B.D=R\{π/2;k ∈ Z}
C.D=R
D.D=R\{π/4+kπ/2;k ∈ Z}
Từ khóa » Cách Tìm Tập Xác định Lớp 11
-
Cách Tìm Tập Xác định Của Hàm Số Lượng Giác Cực Hay - Toán Lớp 11
-
Tìm Tập Xác định Của Hàm Số Lượng Giác ( Có Lời Giải Chi Tiết)
-
Tìm Tập Xác định Của Hàm Số Lượng Giác
-
Phương Pháp Tìm Tập Xác định Của Hàm Số Lượng Giác - Môn Toán 11
-
Cách Tìm Tập Xác định Của Hàm Số Lượng Giác - TopLoigiai
-
Tìm Tập Xác định Của Hàm Số Lượng Giác
-
Tìm Tập Xác định Của Hàm Số Lượng Giác
-
Tổng Hợp Tìm Tập Xác định Của Hàm Số Lớp 11 | Bán Máy Nước Nóng
-
Cách Tìm Tập Xác định, Tập Giá Trị Của Hàm Số Lượng Giác Cực Hay
-
Đại Số Lớp 11: Tập Xác định Của Hàm Số Lượng Giác
-
Cách Tìm Tập Xác định Của Hàm Số Lớp 11?
-
Cách Tìm Tập Xác định Của Hàm Số Lượng Giác
-
Cách Tìm Tập Xác định Của Hàm Số Lượng Giác Lớp 11
-
Cách Tìm Tập Xác định, Tập Giá Trị Của Hàm Số ...