Cách Tìm Trọng Tâm Của Một Hình Không đều. Vị Trí Của ...
Có thể bạn quan tâm
Hình chữ nhật. Vì hình chữ nhật có hai trục đối xứng nên trọng tâm của nó nằm ở giao điểm của các trục đối xứng, tức là tại giao điểm của các đường chéo của hình chữ nhật. 
Tam giác. Trọng tâm nằm ở giao điểm của các trung tuyến của nó. Từ hình học, người ta biết rằng các trung tuyến của một tam giác cắt nhau tại một điểm và chia theo tỷ lệ 1: 2 so với đáy. 
Một vòng tròn. Vì đường tròn có hai trục đối xứng nên trọng tâm của nó là giao điểm của các trục đối xứng.
Hình bán nguyệt. Hình bán nguyệt có một trục đối xứng thì trọng tâm nằm trên trục này. Một tọa độ khác của trọng tâm được tính theo công thức:. 
Nhiều yếu tố cấu trúc được làm từ các sản phẩm cán tiêu chuẩn - góc, dầm chữ I, kênh và các sản phẩm khác. Tất cả các kích thước, cũng như các đặc điểm hình học của cấu hình cuộn, là dữ liệu dạng bảng có thể được tìm thấy trong tài liệu tham khảo trong các bảng phân loại tiêu chuẩn (GOST 8239-89, GOST 8240-89).



ví dụ 1 Xác định vị trí đặt trọng tâm của hình vẽ trên.
Quyết định: 
Chúng tôi chọn các trục tọa độ sao cho trục Ox đi dọc theo kích thước tổng thể cực dưới và trục Oy - dọc theo kích thước tổng thể cực bên trái.
Chúng tôi chia một số phức tạp thành số lượng tối thiểu các hình đơn giản:
hình chữ nhật 20x10;
tam giác 15x10;
đường tròn R = 3 cm.
Chúng tôi tính diện tích của mỗi hình đơn giản, tọa độ trọng tâm của nó. Kết quả của các phép tính được nhập vào bảng
| Hình không. | Diện tích hình A | Tọa độ trọng tâm | |
|
| |||
Trả lời: C (14,5; 4,5)
Ví dụ 2 . Xác định tọa độ trọng tâm của một mặt cắt liên hợp gồm một tấm và các biên dạng cuộn. 
Quyết định.
Chúng tôi chọn các trục tọa độ, như thể hiện trong hình.
Chúng tôi biểu thị các số liệu bằng số và viết ra các dữ liệu cần thiết từ bảng:
| Hình không. | Diện tích hình A | Tọa độ trọng tâm | |
|
| |||
|
| |||
Chúng tôi tính tọa độ trọng tâm của hình bằng công thức:
Trả lời: C (0; 10)
Phòng thí nghiệm công trình số 1 "Xác định trọng tâm của các hình phẳng ghép"
Mục tiêu: Xác định trọng tâm của một hình phức phẳng đã cho bằng phương pháp thực nghiệm và giải tích rồi so sánh kết quả của chúng.
Trình tự công việc
Chia hình thành số hình tối thiểu, trọng tâm của hình đó, ta biết cách xác định.
Cho biết số diện tích và tọa độ trọng tâm của mỗi hình.
Tính tọa độ trọng tâm của mỗi hình.
Tính diện tích của mỗi hình.
Tính tọa độ của trọng tâm của toàn bộ hình bằng công thức (đưa vị trí của trọng tâm trên hình vẽ bên):
Vẽ vào sổ tay hình phẳng của bạn với kích thước, chỉ ra các trục tọa độ.
Xác định trọng tâm bằng phương pháp phân tích.
Lắp đặt thí nghiệm xác định tọa độ của trọng tâm bằng hệ thống treo bao gồm một giá đỡ thẳng đứng 1 (xem hình) mà kim được gắn vào 2 . hình phẳng 3 Làm bằng bìa cứng, dễ chọc thủng lỗ. hố NHƯNG và TẠI đâm xuyên tại các điểm nằm ngẫu nhiên (tốt nhất là ở khoảng cách xa nhau nhất). Một hình phẳng được treo trên một cây kim, đầu tiên tại một điểm NHƯNG , và sau đó ở điểm TẠI . Với sự giúp đỡ của một cái ống nước 4 , được cố định trên cùng một chiếc kim, một đường thẳng đứng được vẽ trên hình bằng bút chì tương ứng với đường dây dọi. Trung tâm của lực hấp dẫn Với Hình sẽ nằm ở giao điểm của các đường thẳng đứng được vẽ khi treo hình tại các điểm NHƯNG và TẠI . 
Trung tâm của lực hấp dẫn Vật cứng là một điểm hình học được liên kết cứng với vật này và là tâm của các lực hấp dẫn song song tác dụng lên các hạt cơ bản riêng lẻ của vật (Hình 1.6).
Vectơ bán kính của điểm này

Hình 1.6
Đối với vật thể đồng chất, vị trí trọng tâm của vật thể không phụ thuộc vào vật liệu mà do hình dạng hình học của vật thể xác định.
Nếu trọng lượng riêng của một vật đồng chất γ , trọng lượng của hạt cơ bản của cơ thể
P k = γΔV k (P = γV ) thay thế vào công thức để xác định r C , chúng ta có
Từ đó, chiếu lên các trục và đi qua giới hạn, ta thu được tọa độ trọng tâm của một khối đồng chất

Tương tự, đối với tọa độ trọng tâm của một mặt đồng chất có diện tích S (Hình 1.7, a)


Hình 1.7
Đối với tọa độ của trọng tâm của một đoạn thẳng đồng chất có độ dài L (Hình 1.7, b)

Phương pháp xác định tọa độ trọng tâm
Dựa vào các công thức tổng quát đã có trước đó, có thể nêu phương pháp xác định tọa độ trọng tâm của vật rắn:
1 Phân tích(bằng cách tích hợp).
2 Phương pháp đối xứng. Nếu vật thể có mặt phẳng, trục hoặc tâm đối xứng thì trọng tâm của nó lần lượt nằm trong mặt phẳng đối xứng, trục đối xứng hoặc tâm đối xứng.
3 Thực nghiệm(phương pháp treo cơ thể).
4 tách ra. Cơ thể được chia thành một số phần hữu hạn, với mỗi phần là vị trí của trọng tâm C và khu vực S đã biết. Ví dụ, hình chiếu của một cơ thể lên một mặt phẳng xOy (Hình 1.8) có thể được biểu diễn dưới dạng hai hình phẳng có diện tích S 1 và S 2 (S = S 1 + S 2 ). Trọng tâm của các hình này nằm ở điểm C 1 (x 1 , y 1 ) và C 2 (x 2 , y 2 ) . Khi đó tọa độ trọng tâm của vật là


Hình 1.8
5Phép cộng(phương pháp diện tích hoặc thể tích âm). Một trường hợp đặc biệt của phương pháp phân vùng. Nó áp dụng cho các cơ thể có vết cắt nếu biết trọng tâm của cơ thể không có vết cắt và vết cắt. Ví dụ, bạn cần tìm tọa độ trọng tâm của một hình phẳng (Hình 1.9):


Hình 1.9
Trọng tâm của các hình đơn giản nhất

Hình 1.10
1 hình tam giác
Trọng tâm của diện tích tam giác trùng với giao điểm của các đường trung trực của nó (Hình 1.10, a).
DM = MB , CM = (1/3)sáng .
2 Cung của một vòng tròn
Cung tròn có trục đối xứng (Hình 1.10, b). Trọng tâm nằm trên trục này, tức là y C = 0 .

dl - phần tử vòng cung, dl = Rdφ , R là bán kính của hình tròn, x = Rcosφ , L = 2aR ,
Vì thế:
x C = R (sinα / α) .
3 Khu vực tròn
Khu vực bán kính R với góc trung tâm 2 α có một trục đối xứng Con bò , trên đó có trọng tâm (Hình 1.10, c).
Chúng tôi chia khu vực thành các khu vực cơ bản, có thể được coi là hình tam giác. Trọng tâm của các cung sơ cấp đều nằm trên cung tròn bán kính (2/3) R .
Trọng tâm của khu vực trùng với trọng tâm của cung AB :
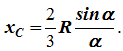
14. Các phương pháp xác định chuyển động của một điểm.
Với phương pháp véc tơ xác định chuyển động, vị trí của một điểm được xác định bằng véc tơ bán kính vẽ từ một điểm cố định trong hệ quy chiếu đã chọn.
Với phương pháp tọa độ xác định chuyển động, tọa độ của một điểm được xác định như một hàm của thời gian:

Đây là các phương trình tham số của quỹ đạo của một chất điểm chuyển động, trong đó thời gian đóng vai trò của một tham số t . Để viết ra phương trình của nó ở dạng rõ ràng, cần phải loại trừ chúng t .
Với cách xác định tự nhiên chuyển động, quỹ đạo của điểm, gốc tọa độ trên quỹ đạo với dấu hiệu là chiều dương của quy chiếu, quy luật thay đổi của tọa độ cung được thiết lập: s = s (t) . Phương pháp này rất tiện lợi khi sử dụng nếu biết trước quỹ đạo của điểm.
15. 1.2 Tốc độ điểm
Coi chuyển động của một điểm trong một khoảng thời gian nhỏ Δt :
![]()
tốc độ trung bình của một điểm trong một khoảng thời gian Dt . Tốc độ của một điểm tại một thời điểm nhất định


Tốc độ điểm là số đo động năng của chuyển động của nó, bằng đạo hàm theo thời gian của vectơ bán kính của điểm này trong hệ quy chiếu đang xét. Vectơ vận tốc hướng tiếp tuyến với quỹ đạo của chất điểm theo hướng chuyển động.
Tác giả: Hãy lấy một cơ thể hình dạng tùy ý. Có thể treo nó trên một sợi để sau khi treo nó vẫn giữ nguyên vị trí của nó (tức là không bắt đầu quay) khi không tí nàođịnh hướng ban đầu (hình 27.1)?
Nói cách khác, có một điểm như vậy, liên quan đến tổng các mômen của các lực hấp dẫn tác động lên các phần khác nhau của cơ thể, sẽ bằng không tại không tí nàođịnh hướng của cơ thể trong không gian?
Người đọc: Vâng tôi cũng nghĩ thế. Điểm như vậy được gọi là trọng tâm của cơ thể.
Bằng chứng.Để đơn giản, hãy xem xét một vật thể ở dạng một tấm phẳng có hình dạng tùy ý được định hướng tùy ý trong không gian (Hình 27.2). Lấy hệ tọa độ X 0tại với gốc tọa độ tại tâm - một điểm Với, sau đó x C = 0, tại C = 0.
 Chúng tôi đại diện cho cơ thể này như một tập hợp của một số lượng lớn các khối điểm tôi, vị trí của mỗi trong số đó được cho bởi vectơ bán kính.
Chúng tôi đại diện cho cơ thể này như một tập hợp của một số lượng lớn các khối điểm tôi, vị trí của mỗi trong số đó được cho bởi vectơ bán kính.
Theo định nghĩa của khối tâm và tọa độ x C = .
Vì trong hệ tọa độ của chúng ta x C= 0, sau đó. Hãy nhân phương trình này với g và lấy
Như có thể thấy từ hình. 27,2, | x tôi| là bờ vai của sức mạnh. Và nếu x tôi> 0, thì mômen của lực Tôi tôi> 0 và nếu x j < 0, то Mj < 0, поэтому с учетом знака можно утверждать, что для любого x tôi thời điểm của lực lượng sẽ là M i = m i gx i. Khi đó đẳng thức (1) tương đương với, trong đó Tôi tôi là mômen của trọng lực. Và điều này có nghĩa là với sự định hướng tùy ý của cơ thể, tổng các mômen của lực hấp dẫn tác dụng lên cơ thể sẽ bằng 0 so với khối tâm của nó.
Để cho cơ thể chúng ta đang xem xét ở trạng thái cân bằng, cần phải áp dụng cho nó tại một điểm Với lực lượng T = mg hướng thẳng đứng lên trên. Thời điểm của lực này về điểm Với bằng không.
Vì lý luận của chúng tôi không phụ thuộc vào bất kỳ cách nào vào cách định hướng chính xác của cơ thể trong không gian, chúng tôi đã chứng minh rằng trọng tâm trùng với khối tâm, đó là điều cần phải chứng minh.
Bài toán 27.1. Tìm trọng tâm của một thanh không trọng lượng có chiều dài l, ở hai đầu của hai khối lượng điểm được cố định t 1 và t 2 .
| t 1 t 2 l | Quyết định. Chúng ta sẽ không tìm trọng tâm mà tìm trọng tâm (vì chúng là một và giống nhau). Hãy giới thiệu trục X(Hình 27.3). |
| x C =? |
Trả lời: xa khối lượng t 1 .
NGỪNG LẠI! Tự quyết định: B1-B3.
Tuyên bố 1 . Nếu một vật phẳng đồng chất có trục đối xứng thì trọng tâm nằm trên trục này.
Thật vậy, đối với bất kỳ khối lượng điểm nào tôi, nằm ở bên phải của trục đối xứng, có cùng một khối lượng điểm nằm đối xứng với khối đầu tiên (Hình 27.4). Trong trường hợp này, tổng các mômen của các lực.
Vì toàn bộ cơ thể có thể được biểu diễn thành các cặp điểm giống nhau, nên tổng mômen trọng lực so với bất kỳ điểm nào nằm trên trục đối xứng bằng không, có nghĩa là trọng tâm của cơ thể cũng nằm trên trục này. Điều này dẫn đến một kết luận quan trọng: nếu vật thể có một số trục đối xứng, thì trọng tâm nằm ở giao điểm của các trục này(Hình 27.5).
Cơm. 27,5 
Tuyên bố 2. Nếu hai vật có khối lượng t 1 và t 2 được kết nối thành một, khi đó trọng tâm của một vật như vậy sẽ nằm trên một đường thẳng nối giữa trọng tâm của vật thứ nhất và thứ hai (Hình 27.6).
Cơm. 27,6 ![]() Cơm. 27,7
Cơm. 27,7
Bằng chứng. Chúng ta hãy sắp xếp vật thể tổng hợp sao cho đoạn nối trọng tâm của các vật thể là phương thẳng đứng. Khi đó tổng các mômen trọng lực của vật thứ nhất đối với chất điểm Với 1 bằng 0 và tổng các mômen hấp dẫn của vật thứ hai về điểm Với 2 là 0 (Hình 27.7).
thông báo rằng vai trọng lực của bất kỳ khối lượng điểm nào t tôi tương tự đối với bất kỳ điểm nào trên phân khúc Với 1 Với 2, và do đó mômen trọng lực so với bất kỳ điểm nào nằm trên đoạn Với 1 Với 2 cái giống nhau. Do đó, trọng lực của toàn bộ cơ thể bằng 0 đối với bất kỳ điểm nào trên đoạn Với 1 Với 2. Như vậy, trọng tâm của vật thể hỗn hợp nằm trên đoạn Với 1 Với 2 .
Tuyên bố 2 ngụ ý một kết luận thực tế quan trọng, được trình bày rõ ràng dưới dạng hướng dẫn.
hướng dẫn,
Làm thế nào để tìm trọng tâm của một vật cứng nếu nó có thể bị phá vỡ
thành các phần, vị trí của các trọng tâm của mỗi phần đã biết
1. Thay mỗi bộ phận bằng một khối lượng nằm ở trọng tâm của bộ phận đó.
2. Tìm Trung tâm của lực hấp dẫn(và điều này giống với trọng tâm) của hệ kết quả là các khối lượng điểm, chọn một hệ tọa độ thuận tiện X 0tại, theo công thức:
Thật vậy, chúng ta hãy định vị phần thân phức hợp sao cho đoạn Với 1 Với 2 nằm ngang, và chúng tôi sẽ treo nó trên các chủ đề tại các điểm Với 1 và Với 2 (Hình 27.8, một). Rõ ràng là cơ thể sẽ ở trạng thái cân bằng. Và sự cân bằng này sẽ không bị xáo trộn nếu chúng ta thay thế mỗi cơ thể bằng các khối điểm t 1 và t 2 (Hình 27.8, b).
 Cơm. 27,8
Cơm. 27,8
NGỪNG LẠI! Hãy tự quyết định: C3.
Bài toán 27.2. Viên bi khối lượng được đặt ở hai đỉnh của một tam giác đều t tất cả mọi người. Đỉnh thứ ba chứa một quả cầu khối lượng 2 t(Hình 27.9, một). Cạnh tam giác một. Xác định trọng tâm của hệ này.
| t 2t một |  Cơm. 27,9 Cơm. 27,9 |
| x C = ? tại C = ? |
Quyết định. Chúng tôi giới thiệu hệ tọa độ X 0tại(Hình 27.9, b). sau đó
,
 .
.
Trả lời: x C = một/2; ; trọng tâm nằm ở nửa chiều cao QUẢNG CÁO.
Khả năng giữ thăng bằng mà không cần nỗ lực là rất quan trọng để thiền, yoga, khí công và múa bụng hiệu quả. Đây là yêu cầu đầu tiên mà người mới bắt đầu phải đối mặt trong các loại hoạt động này và là một trong những lý do tại sao rất khó thực hiện những bước đầu tiên mà không có người hướng dẫn. Một câu hỏi gợi ý rằng một người không biết trọng tâm của mình có thể trông hơi khác. Ví dụ, trong khí công, một người sẽ hỏi làm thế nào để được thư giãn và vẫn thực hiện các động tác khi đứng, một vũ công phương Đông mới bắt đầu sẽ không hiểu cách tách và phối hợp các chuyển động của phần dưới và phần trên của cơ thể, và trong cả hai trường hợp, mọi người sẽ gắng sức quá mức và thường mất thăng bằng. Chuyển động của họ sẽ không chắc chắn, vụng về.
Vì vậy, điều quan trọng là phải hiểu cách tự mình tìm ra trọng tâm, điều này đòi hỏi cả lao động trí óc và kỹ năng, nhưng theo thời gian kỹ năng chuyển sang mức bản năng.
Cần phải làm gì để không bị căng cơ, đồng thời không phải dùng đến các dụng cụ hỗ trợ bên ngoài. Câu trả lời là hiển nhiên, bạn cần phải di chuyển hỗ trợ vào bên trong. Chính xác hơn là dựa vào một trục bên trong có điều kiện. Trục này đi đâu? Khái niệm trọng tâm là có điều kiện, nhưng nó vẫn được sử dụng trong vật lý. Ở đó, người ta thường định nghĩa nó như là điểm ứng dụng của các lực hấp dẫn. Kết quả của lực hấp dẫn là tổng của tất cả các lực hấp dẫn, có tính đến hướng tác động của chúng.
Nó có khó khăn cho đến nay không? Tích trữ sự kiên nhẫn.
Đó là, chúng ta đang tìm kiếm một điểm trên cơ thể cho phép chúng ta không bị ngã, mà không có ý thức chống lại lực hấp dẫn. Điều này có nghĩa là lực hấp dẫn của trái đất phải được điều hướng để nó hội tụ với phần còn lại của lực tác động ở đâu đó trong tâm cơ thể chúng ta.

Hướng của lực như vậy tạo ra một trục có điều kiện ở chính tâm của cơ thể chúng ta, một mặt thẳng đứng, đây là phương thẳng đứng của trọng tâm. Phần cơ thể mà chúng ta dựa vào mặt đất là dấu chân của chúng ta (chúng ta dựa vào mặt đất bằng bàn chân của mình). Ở nơi mà phương thẳng đứng này dựa vào bề mặt mà chúng ta đứng, tức là chúng ta dựa vào mặt đất, đây là trọng tâm của điểm bên trong dấu chân. Nếu phương thẳng đứng dịch chuyển từ nơi này, chúng ta sẽ mất thăng bằng và ngã. Bản thân vùng hỗ trợ càng lớn, chúng ta càng dễ dàng ở gần tâm của nó, và do đó chúng ta sẽ tiến một bước dài theo bản năng khi đứng trên một bề mặt không ổn định. Nghĩa là, khu vực hỗ trợ của \ u200b \ u200 không chỉ là bàn chân mà còn là không gian giữa chúng.

Cũng cần biết rằng chiều rộng của khu vực \ u200b \ u200b khu vực hỗ trợ ảnh hưởng nhiều hơn chiều dài. Trong trường hợp của con người, điều này có nghĩa là chúng ta có nhiều khả năng ngã về phía mình hơn là lùi về phía sau, và thậm chí còn nhiều hơn về phía trước. Do đó, khi chạy, chúng ta khó giữ thăng bằng hơn, gót chân cũng vậy. Nhưng ở những đôi giày rộng, ổn định thì ngược lại, nó dễ dàng chống lại hơn, thậm chí dễ dàng hơn so với việc đi chân trần hoàn toàn. Tuy nhiên, các hoạt động được đề cập ở phần đầu yêu cầu giày dép rất mềm, nhẹ hoặc không có gì cả. Vì vậy, chúng ta không thể không đi giày.

Vì vậy, việc tìm điểm chính giữa của đường thẳng đứng trên bàn chân của bạn là vô cùng quan trọng. Thông thường, nó không nằm ở trung tâm của bàn chân, như một số người tự động cho rằng, mà ở gần gót chân hơn, ở đâu đó từ trung tâm của bàn chân, đến gót chân. Nhưng đó không phải là tất cả.
Ngoài đường thẳng đứng của trọng tâm, còn có đường nằm ngang, cũng như đường nằm riêng cho các chi. Đường ngang dành cho nữ và nam chạy hơi khác một chút.
Ở phía trước, ở phụ nữ, nó vượt qua thấp hơn và ở nam giới, cao hơn. Ở nam giới, nó chạy ở đâu đó 4-5 ngón tay dưới rốn, và ở phụ nữ, khoảng 10 ngón tay. Phía sau đường nữ chạy gần như một koopchik, và đường nam cao hơn nó khoảng năm ngón tay. Ngoài ra, để ổn định tại thời điểm thiền, điều quan trọng là phải chú ý đến đường tuyệt đối của trọng tâm của đầu gối. Nó nằm trên xương một chút (cẳng chân), nhưng hai hoặc ba ngón tay ở dưới sụn.
Trong lúc thiền, cũng như khi múa bụng, việc dang rộng bàn chân là không tốt lắm, độ rộng tối đa thường tương ứng với độ rộng của vai.
Do đó, bạn cần phải giúp mình một chút với đầu gối, cố gắng xây dựng trục thẳng đứng càng thẳng càng tốt. Đứng trước gương, tìm tất cả những điểm được mô tả trên chính bạn. Đặt hai bàn chân của bạn rộng bằng vai. Thư giãn các cơ ở chân và cơ thể. Sau đó, thẳng lưng mà không làm căng cơ thể, thả lỏng chân bằng cách khuỵu nhẹ đầu gối. Hãy tưởng tượng ba đường thẳng đứng, mỗi đường chạy tại một điểm tương ứng ở phía sau thân, phía trước và xung quanh đầu gối. Cố gắng sắp xếp các điểm sao cho trục trước của thân nằm khoảng giữa trục lưng và đầu gối. Trong trường hợp này, đầu gối không được cong quá mức cho phép, chỉ nên hơi cong và thả lỏng. Tốt hơn là ở trên trọng tâm bên trong khu vực hỗ trợ mà chúng tôi tìm thấy trên bàn chân. Đồng thời, có thể tùy ý đặt tay lên thần hoặc đặt lòng bàn tay vào hông.

Làm thế nào bạn biết rằng bạn đã tìm thấy trọng tâm của bạn?
Bạn sẽ cảm thấy hơi lắc lư, nhưng đồng thời chắc chắn bạn sẽ biết rằng bạn sẽ không bị ngã.
Bài giảng 4. Trọng tâm.
Bài giảng này bao gồm các câu hỏi sau
1. Trọng tâm của vật cứng.
2. Tọa độ trọng tâm của các vật thể không đồng nhất.
3. Tọa độ trọng tâm của các vật thể đồng chất.
4. Phương pháp xác định tọa độ các trọng tâm.
5. Trọng tâm của một số vật thể đồng chất.
Việc nghiên cứu những vấn đề này là cần thiết trong tương lai nhằm nghiên cứu động học chuyển động của các vật thể, có xét đến ma sát trượt và ma sát lăn, động lực học khối tâm của một hệ cơ học, mô men động học, để giải quyết các vấn đề trong môn học. "Sức bền vật liệu".
Đưa các lực song song.
Sau khi đã xem xét sự giảm về trọng tâm của một hệ phẳng và một hệ lực tùy ý trong không gian, chúng ta lại quay trở lại việc xem xét một trường hợp cụ thể của hệ các lực song song.
Đưa hai lực song song.
Trong quá trình xét một hệ lực như vậy, có thể xảy ra ba trường hợp giảm sau đây.
1. Hệ hai lực thẳng hàng. Xét một hệ gồm hai lực song song và hướng cùng chiều P và Q, áp dụng tại các điểm NHƯNG và TẠI. Chúng ta sẽ giả sử rằng các lực vuông góc với đoạn này (Hình 1, một).
Với, thuộc phân khúc AB và thỏa mãn điều kiện:
AC/SW = Q/P.(1)
Vectơ hệ thống chính RC = P + Q modulo bằng tổng của các lực này: RC = P + Q.
Với tính đến (1) bằng 0:MC = P ∙ AC- Q∙ SW = 0.
Do đó, kết quả của việc diễn viên, chúng tôi nhận được: RC ≠ 0, MC= 0. Điều này có nghĩa là vectơ chính tương đương với kết quả đi qua tâm giảm, đó là:
Kết quả của các lực thẳng hàng có giá trị tuyệt đối bằng tổng của chúng và đường tác dụng của nó chia đoạn kết nối các điểm ứng dụng của chúng, tỷ lệ nghịch với mô-đun của các lực này bên trong.
Lưu ý rằng vị trí của điểm Với sẽ không thay đổi nếu lực lượng R và Q quay một gócα. Chấm Với, có thuộc tính này được gọi là tâm của các lực song song.
2. Hệ thống hai phản xạ và không bằng nhau về môđun của các lực. Cầu mong các lực lượng P và Q, áp dụng tại các điểm NHƯNG và TẠI, song song, hướng theo các hướng ngược nhau và không bằng nhau trong mô đun (Hình 1, b).
Hãy để chúng tôi chọn điểm làm trung tâm tham chiếu Với, vẫn thỏa mãn quan hệ (1) và nằm trên cùng một đường thẳng, nhưng nằm ngoài đoạn AB.
Vectơ chính của hệ thống này RC = P + Q modulo bây giờ sẽ bằng sự khác biệt giữa các mô-đun của các vectơ: RC = Q - P.
Khoảnh khắc chính về trung tâm Với vẫn là 0:MC = P ∙ AC- Q∙ SW= 0, vì vậy
Kết quả phản xạ và các lực không bằng nhau về giá trị tuyệt đối thì bằng hiệu của chúng, hướng về một lực lớn hơn, và đường tác dụng của nó chia đoạn nối các điểm ứng dụng của chúng, tỷ lệ nghịch với môđun của các lực này bên ngoài.
Hình 1
3. Hệ thống hai phản xạ và các lực bằng nhau trong môđun. Hãy lấy trường hợp giảm trước đó làm trường hợp ban đầu. Hãy sửa chữa nguồn điện R và buộc Q chúng ta hãy cố gắng mô-đun để buộc R.
Sau đó tại Q → R trong công thức (1) tỷ lệ AC/SW → 1. Điều này có nghĩa là AC → SW, nghĩa là, khoảng cách AC →∞ .
Trong trường hợp này, mô-đun của vectơ chính RC → 0, và môđun của mômen chính không phụ thuộc vào vị trí của tâm giảm và vẫn bằng giá trị ban đầu:
MC = P ∙ AC- Q∙ SW = P ∙ ( AC- SW) =P ∙ NHƯNGB.
Do đó, trong giới hạn, chúng ta đã có được một hệ thống lực mà RC = 0, MC≠ 0, và tâm giảm được loại bỏ đến vô cùng, không thể thay thế tâm này bằng kết quả. Trong hệ thống này, không khó để tìm ra một cặp lực lượng, vì vậy một cặp lực lượng không có kết quả.
Trọng tâm của hệ các lực song song.
Xem xét hệ thống N lực lượng Số Pi, áp dụng tại các điểmA tôi (x tôi , y tôi , z tôi) và song song với trụcOv với vectơ l(Hình 2).
Nếu chúng ta loại trừ trước trường hợp của một hệ tương đương với một cặp lực, thì không khó để chứng minh, dựa trên cơ sở của đoạn trước, sự tồn tại của hệ quả của nó.R.
Xác định tọa độ của tâmC(x c, y c, z c) lực song song, nghĩa là, tọa độ của điểm áp dụng hệ quả của hệ này.
Với mục đích này, chúng tôi sử dụng định lý Varignon, trên cơ sở đó:
M0 (R) = Σ M0(Số Pi).

Hình 2
Véc tơ-mô men của lực có thể được biểu diễn dưới dạng tích chéo, do đó:
M 0 (R) = rc× R = Σ M0i(Số Pi)= Σ ( r tôi× Số Pi ).
Cho rằng R = R v ∙ l, một Số Pi = P vi ∙ lvà sử dụng các thuộc tính của tích vectơ, chúng ta nhận được:
rc × R v ∙ l = Σ ( r tôi × P vi ∙ l),
rc ∙ R v × l = Σ ( r tôi ∙ P vi × l) = Σ ( r tôi ∙ P vi ) × l,
hoặc:
[ r c R v - Σ ( r tôi P vi )] × l= 0.
Biểu thức cuối cùng chỉ hợp lệ nếu biểu thức trong ngoặc vuông bằng 0. Do đó, việc bỏ qua chỉ mụcvvà coi đó là kết quảR = Σ Số Pi , từ đây chúng tôi nhận được:
rc = (Σ Số Pi r tôi )/(Σ Số Pi ).
Chiếu bình đẳng vectơ cuối cùng lên trục tọa độ, chúng ta thu được kết quả mong muốn biểu thức tọa độ trọng tâm của các lực song song:
x c = (Σ Số Pi x tôi)/(Σ Số Pi );
y C = (Σ Số Pi y tôi )/(Σ Số Pi );(2)
z c = (Σ Số Pi z tôi )/(Σ Số Pi ).
Trọng tâm của cơ thể
Tọa độ các trọng tâm của một vật đồng chất.
Cân nhắc trọng lượng cơ thể cứng P và âm lượng V trong hệ tọa độ Oxyz, nơi các trục x và y kết nối với bề mặt trái đất và trục z hướng đến thiên đỉnh.
Nếu chúng ta chia cơ thể thành các phần cơ bản với một khối lượng∆ V tôi thì lực hút sẽ tác dụng lên từng phần của nó∆ Số Pihướng vào tâm trái đất. Giả sử rằng kích thước của cơ thể nhỏ hơn nhiều so với kích thước của Trái đất, khi đó hệ thống các lực tác dụng lên các bộ phận cơ bản của cơ thể có thể được coi là không hội tụ, mà song song (Hình 3), và tất cả các kết luận của chương trước có thể áp dụng cho nó.

Hình 3
Sự định nghĩa . Trọng tâm của một vật cứng là trọng tâm của các lực hấp dẫn song song của các bộ phận cơ bản của vật này.
Nhớ lại điều đó trọng lượng riêng phần cơ bản của cơ thể được gọi là tỷ lệ trọng lượng của nó∆ Số Piđến khối lượng ∆ V tôi : γ tôi = ∆ Số Pi/ ∆ V tôi . Đối với một thể đồng nhất, giá trị này là không đổi:γ tôi = γ = P/ V.
Thay vào (2) ∆ Số Pi = γ tôi ∙∆ V tôi thay vì Số Pi, có tính đến nhận xét cuối cùng và giảm tử số và mẫu sốg, chúng tôi nhận được biểu thức tọa độ trọng tâm của một vật đồng chất:
x c = (Σ ∆ Vi∙ x tôi)/(Σ ∆ Vi);
y C = (Σ ∆ Vi∙ y tôi )/(Σ ∆ Vi);(3)
z c = (Σ ∆ Vi∙ z tôi )/(Σ ∆ Vi).
Một số định lý hữu ích trong việc xác định trọng tâm.
1) Nếu một vật đồng chất có mặt phẳng đối xứng thì trọng tâm của nó nằm trong mặt phẳng này.
Nếu các trục X và tạiđược đặt trong mặt phẳng đối xứng này, sau đó đối với mỗi điểm có tọa độ. và phối hợp theo (3), sẽ bằng 0, bởi vì Tổng cộng tất cả các các thuật ngữ có dấu hiệu trái ngược nhau bị loại bỏ theo từng cặp. Vậy trọng tâm là trong mặt phẳng đối xứng.
2) Nếu một vật đồng chất có trục đối xứng thì trọng tâm của vật đó nằm trên trục này.
Thật vậy, trong trường hợp này, nếu trụczvẽ dọc theo trục đối xứng, cho mỗi điểm có tọa độbạn có thể tìm thấy một điểm có tọa độ và tọa độ và tính theo công thức (3) sẽ bằng không.
Định lý thứ ba được chứng minh tương tự.
3) Nếu một vật đồng chất có tâm đối xứng thì trọng tâm của vật đó nằm ở điểm này.
Và một vài nhận xét nữa.
Ngày thứ nhất. Nếu cơ thể có thể được chia thành các phần đã biết trọng lượng và vị trí của trọng tâm thì không cần xét từng điểm mà tính theo công thức (3) Số Pi - được xác định là trọng lượng của bộ phận liên quan vànhư là tọa độ của trọng tâm của nó.
Thứ hai. Nếu cơ thể là đồng nhất, thì trọng lượng của một phần riêng biệt của nó, ở đâu là trọng lượng riêng của vật liệu mà từ đó cơ thể được tạo ra, và Vi - thể tích của phần này của cơ thể. Và công thức (3) sẽ có dạng tiện lợi hơn. Ví dụ,
Và tương tự, ở đâu - khối lượng của toàn bộ cơ thể.
Lưu ý thứ ba. Để cơ thể giống như một tấm mỏng có diện tích F và độ dày t nằm trong máy bay Oxy. Thay thế thành (3)∆ V tôi =t ∙ ∆F tôi , chúng ta thu được tọa độ của trọng tâm của một tấm đồng chất:
x c = (Σ ∆ F tôi∙ x tôi) / (Σ ∆ F tôi);
y C = (Σ ∆ F tôi∙ y tôi ) / (Σ ∆ F tôi).
z c = (Σ ∆ F tôi∙ z tôi ) / (Σ ∆ F tôi).
ở đâu - tọa độ trọng tâm của các tấm riêng lẻ;là tổng diện tích của cơ thể.
Lưu ý thứ tư. Đối với cơ thể ở dạng thanh cong mỏng có chiều dài L với diện tích mặt cắt ngang một khối lượng cơ bản∆ V tôi = một ∙∆ L tôi , Đó là lý do tại sao tọa độ của trọng tâm của một thanh cong mỏng sẽ bằng nhau:
x c = (Σ ∆ L tôi∙ x tôi)/(Σ ∆ L tôi);
y C = (Σ ∆ L tôi∙ y tôi )/(Σ ∆ L tôi);(4)
z c = (Σ ∆ L tôi∙ z tôi )/(Σ ∆ L tôi).
ở đâu - tọa độ của trọng tâmtôi-phần thứ; .
Lưu ý rằng theo định nghĩa, trọng tâm là một điểm hình học; nó cũng có thể nằm ngoài giới hạn của một cơ thể nhất định (ví dụ: đối với một chiếc nhẫn).
Ghi chú.
Trong phần này của khóa học, chúng tôi không phân biệt giữa trọng lực, lực hấp dẫn và trọng lượng cơ thể. Trên thực tế, lực hấp dẫn là sự khác biệt giữa lực hấp dẫn của Trái đất và lực ly tâm do chuyển động quay của nó.
Tọa độ trọng tâm của các vật thể không đồng nhất.
Tọa độ trọng tâm chất rắn không đồng nhất(Hình 4) trong hệ quy chiếu đã chọn được xác định như sau:

Hình 4

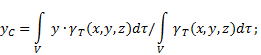

ở đâu - trọng lượng trên một đơn vị thể tích cơ thể (trọng lượng riêng)
![]() - trọng lượng toàn bộ cơ thể.
- trọng lượng toàn bộ cơ thể.
bề mặt không đồng đều(Hình 5), sau đó tọa độ của trọng tâm trong hệ quy chiếu đã chọn được xác định như sau:

Hình 5
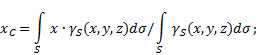

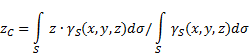
ở đâu - trọng lượng trên một đơn vị diện tích của cơ thể
![]() - trọng lượng toàn bộ cơ thể.
- trọng lượng toàn bộ cơ thể.
Nếu chất rắn là dòng không đồng nhất(Hình 6), sau đó tọa độ của trọng tâm trong hệ quy chiếu đã chọn được xác định như sau:

Hình 6

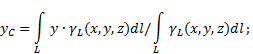

ở đâu - chiều dài cơ thể đơn vị trọng lượng,
Trọng lượng toàn bộ cơ thể.
Phương pháp xác định tọa độ trọng tâm.
Dựa vào các công thức tổng quát thu được ở trên, có thể chỉ ra các phương pháp cụ thể xác định tọa độ trọng tâm của các vật thể.
1. Đối diện. Nếu một vật thể đồng chất có mặt phẳng, trục hoặc tâm đối xứng (Hình 7), thì trọng tâm của nó lần lượt nằm trong mặt phẳng đối xứng, trục đối xứng hoặc tâm đối xứng.

Hình 7
2. Chia tách. Cơ thể được chia thành một số phần hữu hạn (Hình 8), mỗi phần đã biết vị trí của trọng tâm và diện tích.
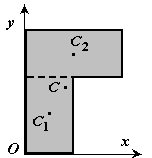
Hình 8
S \ u003d S 1 + S 2.
3.Phương pháp vùng âm. Một trường hợp đặc biệt của phương pháp phân vùng (Hình 9). Nó áp dụng cho các cơ thể có vết cắt nếu biết trọng tâm của cơ thể không có vết cắt và vết cắt. Phần thân ở dạng tấm có đường cắt được biểu thị bằng sự kết hợp của tấm đặc (không có đường cắt) với diện tích S1 và diện tích của phần bị cắt ra S2.

Hình 9
S \ u003d S 1 - S 2.
4.phương pháp phân nhóm. Nó là một bổ sung tốt cho hai phương pháp cuối cùng. Sau khi chia nhỏ hình thành các phần tử cấu thành của nó, có thể thuận tiện khi kết hợp một số phần tử trong số chúng lại, để sau đó đơn giản hóa giải pháp bằng cách tính đến tính đối xứng của nhóm này.
Trọng tâm của một số vật thể đồng chất.
1) Trọng tâm của cung tròn. Xem xét vòng cung AB bán kínhRvới góc trung tâm. Do tính đối xứng, trọng tâm của cung này nằm trên trụcCon bò(Hình 10).

Hình 10
Hãy tìm tọa độ theo công thức . Để làm điều này, hãy chọn trên vòng cung AB thành phần MM ’ Dài, vị trí của nó được xác định bởi góc. Danh từ: Tọa độ X thành phần MM ' sẽ. Thay thế các giá trị này X và d l và lưu ý rằng tích phân phải được mở rộng trên toàn bộ chiều dài của cung, chúng ta nhận được:
![]()
với L là độ dài cung AB bằng.
Từ đây cuối cùng ta thấy rằng trọng tâm của cung tròn nằm trên trục đối xứng của nó cách tâm một khoảngỒ bằng nhau
góc ở đâu đo bằng radian.
2) Trọng tâm của diện tích một tam giác. Xét một tam giác nằm trong mặt phẳng Oxy, tọa độ đỉnh đã biết: A tôi (x tôi,y tôi ), (tôi= 1,2,3). Bẻ hình tam giác thành các dải hẹp song song với cạnh bên NHƯNG 1 NHƯNG 2, ta đi đến kết luận trọng tâm của tam giác phải thuộc đường trung tuyến. NHƯNG 3 M 3 (hình 11).

Hình 11
Bẻ hình tam giác thành các dải song song với cạnh bên NHƯNG 2 NHƯNG 3, bạn có thể đảm bảo rằng nó phải nằm trên dải phân cách NHƯNG 1 M một . Vì vậy, trọng tâm của một tam giác nằm ở giao điểm của các đường trung tuyến của nó, như bạn đã biết, tách phần thứ ba khỏi mỗi trung vị, tính từ cạnh tương ứng.
Đặc biệt, đối với dải phân cách NHƯNG 1 M 1 chúng tôi nhận được, cho rằng tọa độ của điểm M 1 - là trung bình cộng của tọa độ các đỉnh NHƯNG 2 và NHƯNG 3 :
x c = x 1 + (2/3) ∙ (xM 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.
Như vậy, tọa độ trọng tâm của tam giác là trung bình cộng của tọa độ các đỉnh của nó:
x c =(1/3) Σ x tôi ; y c =(1/3) Σ y tôi .
3) Trọng tâm của diện tích hình tròn. Xét một cung của một hình tròn bán kính R với góc trung tâm 2α , nằm đối xứng qua trục Con bò (Hình 12).
Hiển nhiên là y c = 0, và khoảng cách từ tâm của hình tròn mà từ đó khu vực này bị cắt đến trọng tâm của nó có thể được xác định theo công thức:

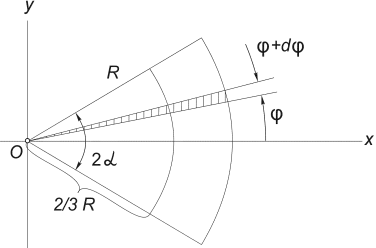
Hình 12
Cách dễ nhất để tính tích phân này là chia miền tích phân thành các cung cơ bản với một góc dφ . Tối đa là các chỉ số nhỏ nhất của bậc đầu tiên, một khu vực như vậy có thể được thay thế bằng một hình tam giác có cơ sở bằng R × dφ và chiều cao R. Diện tích của một tam giác như vậy dF =(1/2)R 2 ∙ dφ , và trọng tâm của nó là 2/3 R từ trên cùng, vì vậy trong (5) chúng tôi đặt x = (2/3)R∙ cos. Thay thế thành (5) F= α R 2, chúng tôi nhận được:
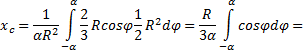
Sử dụng công thức cuối cùng, chúng tôi tính toán, cụ thể là khoảng cách đến trọng tâm hình bán nguyệt.
Thay vào (2) α = π / 2, ta được: x c = (4 R) / (3 π) ≅ 0,4 R .
ví dụ 1Hãy để chúng tôi xác định trọng tâm của vật thể đồng chất được hiển thị trong hình. mười ba.

Hình 13
Quyết định.Cơ thể đồng nhất, bao gồm hai phần có hình dạng đối xứng. Tọa độ trọng tâm của chúng:
Khối lượng của họ:
Do đó, tọa độ trọng tâm của cơ thể
Ví dụ 2 Tìm trọng tâm của một tấm bị uốn một góc vuông. Kích thước - trên bản vẽ (Hình 14).

Hình 14
Quyết định. Các tâm tọa độ trọng lực:
0.
Hình vuông:
Cho nên:
Ví dụ 3 Trên một tờ giấy vuôngcm cắt lỗ vuôngxem (Hình 15). Tìm trọng tâm của tấm. Ví dụ 4 Tìm vị trí của trọng tâm của tấm được chỉ ra trong hình. 16. Kích thước được cho bằng cm.

Hình 16
Quyết định. Chúng tôi chia tấm thành các hình (Hình 17), trung tâm mức độ nghiêm trọng của ai đã được biết.
Diện tích của những hình này và tọa độ của trọng tâm của chúng:
1) một hình chữ nhật với các cạnh 30 và 40 cm,S 1 =30 ∙ 40 = 1200 cm 2 ; x 1= 15 cm; tại 1 \ u003d 20 cm.
2) một tam giác vuông có đáy là 50 cm và chiều cao là 40 cm;S 2 =0,5 ∙ 50 ∙ 40 = 1000 cm 2 ; X 2 \ u003d 30 + 50/3 \ u003d 46,7 cm; y 2 =40/3 = 13,3 cm;
3) bán kính nửa đường tròn r = 20 cm;S 3 =0,5 ∙π∙ 20 2 \ u003d 628 cm 2 ; X 3 =4 R /3 π = 8,5 cm; tại
Quyết định. Nhớ lại rằng trong vật lý, mật độ của một cơ thểρ và trọng lượng riêng của nógliên quan theo tỷ lệ:γ = ρ g , ở đâug - Gia tốc trọng lực. Để tìm khối lượng của một vật thể đồng nhất như vậy, bạn cần nhân khối lượng riêng với thể tích của nó.

Hình 19
Thuật ngữ mật độ "tuyến tính" hoặc "tuyến tính" có nghĩa là để xác định khối lượng của thanh giàn, mật độ tuyến tính phải được nhân với chiều dài của thanh này.
Để giải quyết vấn đề, bạn có thể sử dụng phương pháp phân vùng. Biểu diễn một giàn đã cho dưới dạng tổng của 6 thanh riêng lẻ, chúng ta nhận được:
ở đâuL tôi chiều dàitôi - cây gậy thứ của trang trại, vàx tôi , y tôi - tọa độ của trọng tâm của nó.
Giải pháp cho vấn đề này có thể được đơn giản hóa bằng cách nhóm 5 thanh kèo cuối cùng. Dễ dàng nhận thấy chúng tạo thành một hình có tâm đối xứng nằm ở giữa thanh thứ 4, nơi đặt trọng tâm của nhóm thanh này.
Do đó, một giàn nhất định có thể được biểu diễn bằng sự kết hợp của chỉ hai nhóm thanh.
Nhóm đầu tiên bao gồm thanh đầu tiên, cho nóL 1 = 4 m,x 1 = 0 m,y 1 = 2 m. Nhóm que thứ hai gồm năm que tính, trong đóL 2 = 20 m,x 2 = 3 m,y 2 = 2 m.
Tọa độ trọng tâm của trang trại được tìm theo công thức:
x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4 ∙ 0 + 20 ∙ 3) / 24 = 5/2 m;
y c = (L 1 ∙ y 1 + L 2 ∙ y 2 )/(L 1 + L 2 ) = (4 ∙ 2 + 20 ∙ 2) / 24 = 2 m.
Lưu ý rằng trung tâm Với nằm trên đường kết nối Với 1 và Với 2 và chia đoạn Với 1 Với 2 liên quan đến: Với 1 Với/SS 2 = (x c - x 1 )/(x 2 - x c ) = L 2 / L 1 = 2,5/0,5.
Câu hỏi tự kiểm tra
Trọng tâm của các lực song song là gì?
- Tọa độ trọng tâm của các lực song song được xác định như thế nào?
- Làm thế nào để xác định được trọng tâm của các lực song song, kết quả của nó bằng 0?
Tính chất của trọng tâm của các lực song song là gì?
- Những công thức nào dùng để tính toạ độ trọng tâm của các lực song song?
Trọng tâm của một vật là gì?
- Tại sao lực hút Trái đất tác dụng lên một điểm của vật có thể coi là hệ các lực song song?
- Viết công thức xác định vị trí trọng tâm của vật không đồng chất và đồng chất, công thức xác định vị trí trọng tâm của tiết diện phẳng?
- Viết công thức xác định vị trí trọng tâm của các hình hình học đơn giản: hình chữ nhật, hình tam giác, hình thang và nửa hình tròn?
Thế nào được gọi là mô men tĩnh của diện tích?
- Nêu ví dụ về vật có trọng tâm nằm ngoài vật.
- Tính chất đối xứng dùng để xác định trọng tâm của các vật như thế nào?
- Thực chất của phương pháp trọng âm là gì?
Trọng tâm của cung tròn nằm ở đâu?
Làm thế nào bạn có thể tìm thấy trọng tâm của một tam giác bằng đồ thị?
- Viết công thức xác định trọng tâm của hình tròn.
- Sử dụng công thức xác định trọng tâm của tam giác và cung tròn, suy ra công thức tương tự đối với đoạn tròn.
- Công thức nào dùng để tính toạ độ trọng tâm của các vật thể đồng chất, hình phẳng và đường thẳng?
- Thế nào gọi là mômen tĩnh của diện tích hình phẳng so với trục, nó được tính như thế nào và có chiều như thế nào?
- Làm thế nào để xác định vị trí trọng tâm của khu vực, nếu biết vị trí các trọng tâm của các bộ phận riêng lẻ của nó?
- Định lý bổ trợ nào được sử dụng trong việc xác định vị trí của trọng tâm?
Từ khóa » Cách Vẽ Trọng Tâm Trong Hình Không Gian
-
Trọng Tâm Của Tứ Diện Là Gì? Cách Xác định Trọng Tâm Của Tứ Diện
-
Trọng Tâm Của Tứ Diện Là Gì? - Toán Học Việt Nam - MathVn.Com
-
Trọng Tâm Là Gì? Công Thức Tính Trọng Tâm Của Tam Giác
-
Trọng Tâm Là Gì? Các Tính Chất Của Trọng Tâm Tam Giác, Hình Thang, Tứ ...
-
Trọng Tâm Của Tứ Diện Trong Không Gian
-
Tính Chất Của Trọng Tâm Và Cách Xác định Trọng Tâm Trong Hình Học
-
Kiến Thức Cách Vẽ Trọng Tâm Của Tam Giác | Bán Máy Nước Nóng
-
Toạ độ Trọng Tâm Của Tam Giác Trong Không Gian
-
LÝ THUYẾT TRỌNG Tâm HÌNH Học KHÔNG GIAN - Tài Liệu Text
-
HÌNH KHÔNG GIAN TRỌNG TÂM- THẦY NGUYỄN TIẾN ĐẠT
-
Cách Xác định Trọng Tâm Của Một Hình Không đều. Tìm ...
-
Các Nguyên Tắc Vẽ Hình Học Không Gian Mà Bạn Cần Phải Biết
-
Nguyên Tắc Cơ Bản Trong Vẽ Hình Học Không Gian Và Lưu ý - Facebook