Cách Tính Diện Tích Và Thể Tích Của Hình Nón, Hình Nón Cụt
Có thể bạn quan tâm
Tương tự như hình cầu, hình nón và hình nón cụt cũng là những khối tròn xoay thường gặp trong Toán học cũng như trong thực tiễn.
Đọc thêm: Cách sử dụng GeoGebra để mô hình hóa khái niệm hình nón
Vâng! Nón lá, kem ốc quế, cái quặng, cái xô, đèn ngủ, chậu kiểng, … là những hình ảnh thường gặp nhất và dễ liên tưởng nhất đến hình nón.
Nhằm giúp các bạn có cái nhìn chi tiết hơn về hình nón và hình nón cụt, cũng như để các bạn biết cách tính diện tích xung quanh, diện tích toàn phần và thể tích của hình nón/ hình nón cụt nên mình đã soạn biên rất chi tiết bài viết này.
Ok. Ngay bây giờ chúng ta hãy cùng nhau tìm hiểu nhé …
Mục Lục Nội Dung
- I. Hình nón
- #1. Hình nón là gì?
- #2. Tính chất của hình nón
- #3. Cách tính diện tích xung quanh của hình nón
- #4. Cách tính diện tích toàn phần của hình nón
- #4. Cách tính thể tích của hình nón
- II. Hình nón cụt
- #1. Hình nón cụt là hình gì?
- #2. Cách tính diện tích xung quanh của hình nón cụt
- #3. Cách tính diện tích toàn phần của hình nón cụt
- #3. Cách tính thể tích của hình nón cụt
- III. Lời kết
I. Hình nón
#1. Hình nón là gì?
Định nghĩa: Hình nón là hình được tạo ra khi quay tam giác vuông một vòng quanh một cạnh góc vuông cố định.
Hay hiểu theo một cách khác nữa: Hình nón là hình học không gian 3 chiều đặc biệt, được nối liền với nhau bởi một mặt cong và một đỉnh.
Khi quay tam giác vuông AOC (vuông ở O) một vòng quanh cạnh góc vuông AO cố định chúng ta sẽ được một hình nón
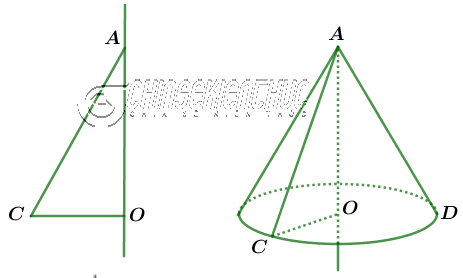
Sau khi quay cạnh …
- OC sẽ tạo ra đáy của hình nón, nó là một hình tròn tâm O bán kính OC
- AC sẽ tạo ra mặt xung quanh của hình nón, mỗi một vị trí của AC được gọi là một đường sinh
A được gọi là đỉnh
AO được gọi là đường cao
#2. Tính chất của hình nón
- Hình nón có một đỉnh hình tam giác.
- Hình nón có trục vuông góc với mặt đáy. Mặt tròn gọi là đáy hình nón.
- Đặc biệt nó không có bất kỳ cạnh nào.
- Chiều cao là khoảng cách từ tâm của vòng tròn đến đỉnh của hình nón. Hình tạo ra bởi đường cao và bán kính trong hình nón sẽ là tam giác vuông.
- Hình nón thì có hình nón tròn và hình nón xiên.
#3. Cách tính diện tích xung quanh của hình nón
Diện tích xung quanh của hình nón sẽ bằng tích của $\pi$, độ dài bán kính, độ dài đường sinh
Công thức: $S_{xq}=\pi.r.l$
Chú ý: Độ dài của đường sinh sẽ bằng căn bậc hai của tổng bình phương độ dài bán kính và chiều cao.
#4. Cách tính diện tích toàn phần của hình nón
Diện tích toàn phần của hình nón sẽ bằng tổng của diện tích xung quanh, diện tích đáy
Công thức: $S_{tp}=S_{xq}+\pi.r^2=\pi.r.l+\pi.r^2$
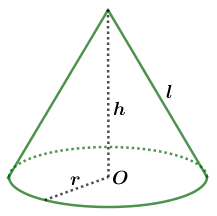
#4. Cách tính thể tích của hình nón
Thể tích của hình nón sẽ bằng tích của một phần ba, $\pi$, bình phương độ dài bán kính, chiều cao
Công thức: $V=\frac{1}{3}.\pi.r^2.h$
Ví dụ 1: Cho hình nón có độ dài bán kính bằng $r=6~cm$ và chiều cao bằng $h=8~cm$
Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình chóp
Lời Giải:
Công việc đầu tiên cần làm là tính độ dài của đường sinh l của hình nón
Độ dài đường sinh l của hình nón đã cho sẽ được tính theo công thức $\sqrt{r^2+h^2}=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10~cm$
 |  |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] | CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
$S_{xq}=\pi.r.l=\pi.6.10=60\pi \approx 188.5~cm^2$
$S_{tp}=S_{xq}+\pi.r^2=60\pi+\pi.6^2=60.\pi+36.\pi=96.\pi \approx 301.6~cm^2$
$V=\frac{1}{3}.\pi.r^2.h=\frac{1}{3}.\pi.6^2.8=96.\pi \approx 301.6~cm^3$
Vậy diện tích xung quanh, diện tích toàn phần và thể tích của hình chóp đã cho lần lượt gần bằng $188.5~cm^2, 301.6~cm^2, 301.6~cm^3$
II. Hình nón cụt
#1. Hình nón cụt là hình gì?
Đinh nghĩa: Hình nón cụt là hình có hai đáy là 2 hình tròn có bán kính to nhỏ khác nhau nằm trên hai mặt phẳng song song, có đường nối tâm là trục đối xứng.
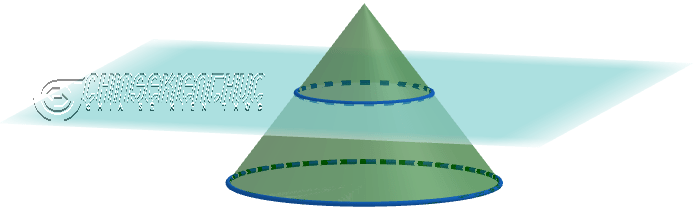
Hay bạn có thể hiểu: Hình nón cụt là một hình nón được cắt bởi mặt phẳng song song với đáy, lúc này phần giữa khung và đáy được gọi là hình nón cụt.
Như các bạn có thể thấy ở hình bên dưới: Khi cắt hình nón bởi một mặt phẳng song song với mặt phẳng đáy (hình tròn đáy) chúng ta sẽ thu được một hình nón cụt.
#2. Cách tính diện tích xung quanh của hình nón cụt
Diện tích xung quanh của hình nón cụt sẽ bằng tích của $\pi$, tổng độ dài hai bán kính, độ dài đường sinh
Công thức: $S_{xq}=\pi.(r_1+r_2).l$
#3. Cách tính diện tích toàn phần của hình nón cụt
Diện tích toàn phần của hình nón cụt sẽ bằng tổng của diện tích xung quanh, diện tích đáy lớn, diện tích đáy bé
Công thức: $S_{tp}=S_{xq}+\pi(r_1^2+r_2^2)= \pi.(r_1+r_2).l +\pi.(r_1^2+r_2^2)$
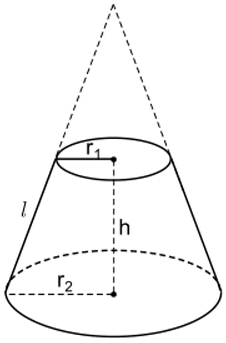
#3. Cách tính thể tích của hình nón cụt
Thể tích của hình nón cụt sẽ bằng / được tính theo công thức $\frac{1}{3}.\pi.h.(r_1^2+r_2^2+r_1.r_2)$
Công thức: $V=\frac{1}{3}.\pi.h.(r_1^2+r_2^2+r_1.r_2)$
Ví dụ 2: Cho một cái xô có dạng hình nón cụt với các kích thước như Hình 1
- a) Tính diện tích xung quanh của xô
- b) Khi xô chứa đầy nước thì dung tích của nó là bao nhiêu
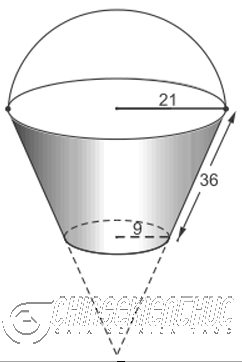
Lời Giải:
2.1. Diện tích xung quanh của xô
Trước hết ta thấy diện tích xung quanh của xô chính bằng diện tích xung quanh của hình nón cụt.
Mà diện tích xung quanh của hình nón cụt lại bằng diện tích xung quanh của hình nón lớn trừ diện tích xung quanh của hình nón nhỏ.
+ Diện tích hình nón lớn:
Gọi l là đường sinh của hình nón lớn.
Áp dụng định lí Ta-lét ta được: $\frac{l}{l-36}=\frac{21}{9} \Rightarrow l=63~cm$
=> Suy ra diện tích xung quanh của hình nón lớn sẽ bằng $\pi.21.63=1323\pi \approx 4156.3~cm^2$
+ Diện tích hình nón nhỏ
Gọi l’ là đường sinh của hình nón nhỏ.
Ta có $l’+36=l \Leftrightarrow l’+36=63 \Leftrightarrow l’=27~cm$
Suy ra diện tích xung quanh của hình nón nhỏ sẽ bằng $\pi.9.27=243\pi \approx 763.4~cm^2$
=> Vậy diện tích xung quanh của hình nón cụt sẽ bằng $1323\pi – 243\pi=1080\pi \approx 3392.9~cm^2$
2.2. Dung tích của xô khi đầy
Trước hết ta thấy dung tích của xô khi chứa đầy nước bằng thể tích của hình nón cụt
Mà thể tích của hình nón cụt lại bằng thể tích của hình nón lớn trừ thể tích của hình nón nhỏ
+ Thể tích của hình nón lớn:
Chiều cao của hình nón lớn sẽ bằng $\sqrt{63^2-21^2}=42\sqrt{2} \approx 59.4~cm$
Suy ra thể tích của hình nón lớn sẽ bằng $\frac{1}{3}.\pi.21^2.42\sqrt{2} \approx 27430.4~cm^3$
+ Thể tích của hình nón nhỏ:
Chiều cao của hình nón nhỏ sẽ bằng $\sqrt{27^2-9^2}=18\sqrt{2} \approx 25.5~cm$
Suy ra thể tích của hình nón nhỏ sẽ bằng $\frac{1}{3}.\pi.9^2.18\sqrt{2} \approx 2159.3~cm^3$
Vậy thể tích của hình nón cụt sẽ bằng $\frac{1}{3}.\pi.21^2.42\sqrt{2}-\frac{1}{3}.\pi.9^2.18\sqrt{2} \approx 25271.1~cm^3$
Vậy diện tích xung quanh của xô, dung tích của xô khi chứa đầy nước lần lượt gần bằng $3392.9~cm^2, 25271.1~cm^3$
Nhận xét:
- Chúng ta đã tính được diện tích xung quanh / thể tích của hình chóp cụt thông qua việc tính hiệu diện tích xung quanh / thể tích của hình chóp lớn và hình chóp nhỏ.
- Ở đây chúng ta không áp dụng trực tiếp công thức tính diện tích xung quanh và thể tích của hình chóp cụt được là vì không có chiều cao.
III. Lời kết
Okay, như vậy là qua bài viết này bạn đã biết cách tích diện tích hình nón, diện tích hình nón cụt, thể tích hình nón và thể tích hình nón cụt rồi nhé.
Như các bạn đã biết, Toán học bắt nguồn từ thực tiễn, Toán học giúp giải quyết các vấn đề trong thực tiễn. Tuy nhiên, việc ứng dụng được kiến thức Toán học thuần túy vào thực tiễn không hề dễ dàng.
Bạn cần có thời gian để hiểu kỹ mảng kiến thức đó và phải biết cách chuyển từ bài toán thực tiễn sang bài toán thuần túy.
Trở lại Ví dụ 2 thì chúng ta có thể nhận thấy là …
- Diện tích xung quanh của xô chính là diện tích xung quanh của hình nón cụt.
- Dung tích của xô khi chứa đầy nước chính là thể tích của hình nón cụt.
- Cần ít nhất bao nhiêu $cm^2$ INOX để làm được một cái xô như vậy chính là diện tích xung quanh của hình nón cụt và diện tích hình tròn ở đáy.
Okay, hi vọng là những kiến thức trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Đọc thêm:
- Cách tính thể tích tứ diện trong không gian (công thức & casio)
- Tính diện tích, thể tích của hình lăng trụ đứng tam giác, tứ giác
- Tính diện tích và thể tích của hình chóp đều, hình chóp cụt đều
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Edit by Kiên Nguyễn
Bài viết đạt: 5/5 sao - (Có 1 lượt đánh giá)Từ khóa » Cách Tính Diện Tích đáy Hình Nón
-
Công Thức Tính Thể Tích Hình Nón, Diện Tích Hình Nón "dễ Nhớ"
-
Công Thức Và Cách Tính Thể Tích Hình Nón Đầy Đủ Nhất
-
Tính Diện Tích Xung Quanh Hình Nón, Diện Tích Toàn Phần, Thể Tích ...
-
Công Thức Tính Diện Tích Xung Quanh Hình Nón, Diện Tích Toàn Phần ...
-
Công Thức Tính Diện Tích Xung Quanh Hình Nón - Luật Hoàng Phi
-
Diện Tích Xung Quanh, Toàn Phần Hình Nón - DBK VIỆT NAM
-
Công Thức Tính Diện Tích Hình Nón, Có Bài Tập Minh Họa - Thủ Thuật
-
Công Thức Tính Diện Tích Xung Quanh Hình Nón - Mobitool
-
Công Thức Tính Thể Tích Hình Nón, Diện Tích Xung Quanh, Toàn Phần ...
-
Công Thức & Diện Tích Toàn Phần Hình Nón
-
Công Thức & Cách Tính Diện Tích Hình Nón - Thủ Thuật Phần Mềm
-
Công Thức Tính: [Diện Tích] [Thể Tích] Hình Nón & Bài Tập Tham Khảo
-
Công Thức Cách Tính Diện Tích Của Hình Nón - YouTube
-
Công Thức Tính Diện Xung Quanh, Diện Tích Toàn Phần Hình Nón