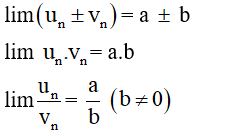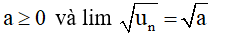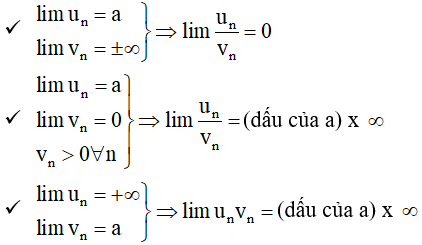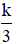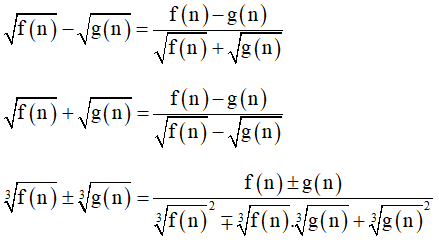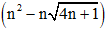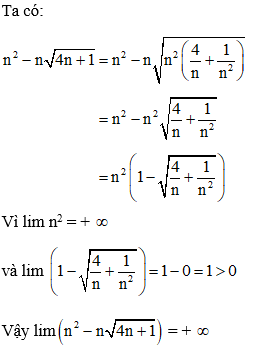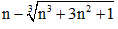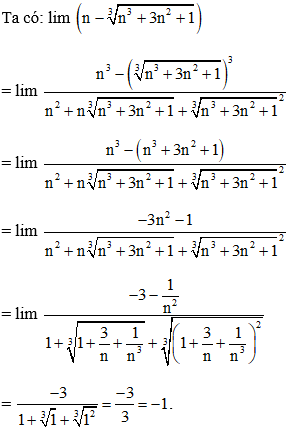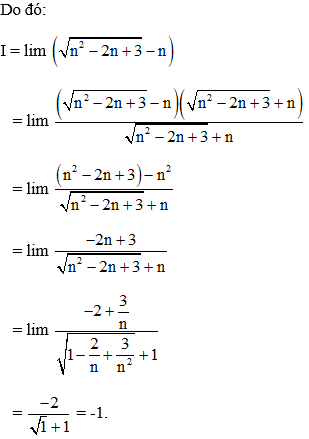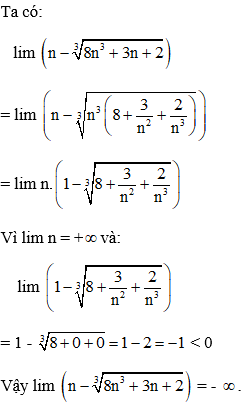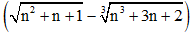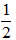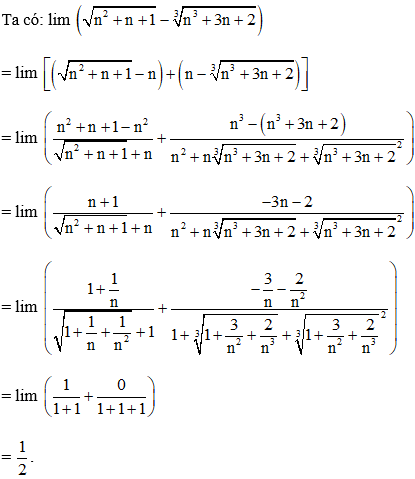Cách Tính Giới Hạn Của Dãy Số Có Chứa Căn ...

Cách tính giới hạn của dãy số có chứa căn thức cực hay, chi tiết

A. Phương pháp giải

+) Sử dụng các kiến thức sau:

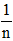
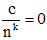
• Với c là hằng số ta có: lim c = c, lim = 0. Tổng quát lim (k ≥ 1).

• Các phép toán trên các dãy có giới hạn hữu hạn

- Nếu lim un = a và lim vn = b thì

  

- Nếu un ≥ 0 với mọi n và lim un = a thì

  

• Các phép toán trên dãy có giới hạn vô cực

  

+) Phương pháp giải:

a) Giới hạn dãy số dạng 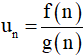, trong đó f(n) và g(n) là các biểu thức chứa căn

=> Chia (các số hạng) của cả tử và mẫu cho lũy thừa của n có số mũ cao nhất trong dãy và dùng các kết quả trên để tính.

Quy ước:

Biểu thức 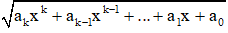có bậc là

Biểu thức 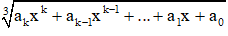có bậc là

b) Giới hạn dãy số dạng 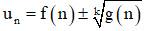với f(n) và g(n) là các đa thức

=> Rút lũy thừa của n có số mũ cao nhất ra và sử dụng kết quả của giới hạn dãy số tại vô cực để tính.

c) Giới hạn của dãy số dạng vô định (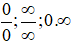) thì ta sử dụng các phép biến đổi liên hợp để đưa dãy số về dạng a) và b).

Các phép biến đổi liên hợp:

B. Ví dụ minh họa

Ví dụ 1: Tính giới hạn: lim

A. - 1

B. 3

C. +∞

D. - ∞

Hướng dẫn giải:

Đáp án C

Ví dụ 2: Giới hạn lim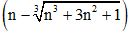 bằng

A. - 1

B. 1

C. + ∞

D. - ∞

Hướng dẫn giải:

Ta tiến hành nhân chia với biểu thức liên hợp bậc ba của biểu thức

Đáp án A

Ví dụ 3: Tính giới hạn

A. I = 1

B. I = - 1

C. I = 0

D. I = + ∞

Hướng dẫn giải:

Ta sử dụng phương pháp nhân với biểu thức liên hợp

Biểu thức liên hợp của biểu thức

Đáp án B

Ví dụ 4: lim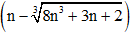 bằng:

A. + ∞

B. - ∞

C. -1

D. 0

Hướng dẫn giải:

Đáp án B

Ví dụ 5: Tính giới hạn lim

A.

B. 0

C. + ∞

D. - ∞

Hướng dẫn giải:

Đáp án A