Cách Tính Thể Tích Hình Trụ - Từ Điển Toán Học
Có thể bạn quan tâm
Hình trụ là gì? Cách tính thể tích hình trụ như thế nào? Những bài tập áp dụng công thức tính thể tích hình trụ sẽ được trình bày trong bài viết sau đây.
Tóm tắt nội dung
- 1. Hình trụ là gì?
- 2. Công thức tính thể tích hình trụ
- 2.1. Tìm bán kính đáy hình trụ
- 2.2. Tính diện tích đáy hình trụ
- 2.3. Tính chiều cao hình trụ
- 2.4. Nhân diện tích đáy với chiều cao
- 3. Bài tập áp dụng để tính thể tích hình trụ
1. Hình trụ là gì?
Hình trụ là hình có hai mặt đáy là hình tròn song song và bằng nhau. Hình trụ được vẽ mô tả như hình bên dưới đây.
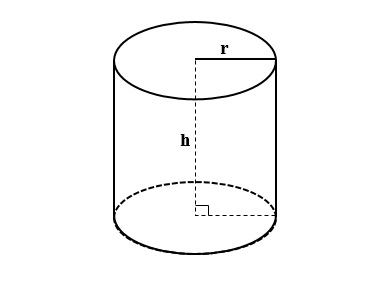
2. Công thức tính thể tích hình trụ
Thể tích hình trụ bằng tích chiều cao với bình phương bán kính hình tròn đáy và số pi. Hoặc thể tích hình trụ bằng diện tích đáy nhân với chiều cao.
Công thức tính thể tích hình trụ: V = Sđáy.h = π.r2.h (m3)
Trong đó:
- V là thể tích hình trụ
- Sđáy là diện tích mặt đáy
- r là bán kính hình tròn đáy
- h là chiều cao hình trụ
- π là số pi, có giá trị bằng 3,14
- Đơn vị thể tích là mét khối (m3)
2.1. Tìm bán kính đáy hình trụ
Bạn có thể tìm bán kính đáy hình trụ bằng cách xác định bán kính của hình tròn bất kỳ cắt ngang hình trụ và vuông góc với chiều cao. Mọi hình tròn được như vậy đều có bán kính bằng với bán kính đáy. Bạn có thể tìm được bán kinh đáy hình trụ bằng các phương pháp sau:
- Đo đường kính mặt đáy rồi chia cho 2, bởi d = 2r
- Nếu biết chu vi hình tròn đáy thì bạn chia cho 2π, bởi C = 2πr
2.2. Tính diện tích đáy hình trụ
Khi biết được giá trị của bán kính đáy thì ta có thể tính được diện tích đáy hình trụ theo công thức sau:
Diện tích đáy hình trụ: Sđáy = π.r2 (m2)
2.3. Tính chiều cao hình trụ
Chiều cao hình trụ được xác định là đoạn thẳng nối hai đáy và vuông góc với đáy hình trụ. Như vậy có vô số đoạn thằng là chiều cao của hình trụ, trong đó có 2 vị trí quan mà ta có thể xác định chiều cao dễ dàng:
- Đoạn thẳng nối tâm hai hình tròn đáy của hình trụ
- Đoạn thằng nối một điểm trên đường tròn đáy và hình chiếu của nó trên hình tròn đáy còn lại của hình trụ
Bằng cách đặt thước vuông góc với mặt đáy và đọc số đo của thước ở mặt đáy còn lại là bạn có thể biết được giá trị của chiều cao hình trụ.
2.4. Nhân diện tích đáy với chiều cao
Sau khi tìm được diện tích đáy và chiều cao của hình trụ, bạn có thể tìm được thể tích hình trụ bằng cách nhân diện tích đáy với chiều cao. Bước này là bước cuối cùng và đơn giản nhất của quá trình tính thể tích hình trụ.
3. Bài tập áp dụng để tính thể tích hình trụ
Bài 1: Một hình trụ có chu vi đáy 30 cm và chiều cao là 10 cm. Hỏi thể tích hình trụ này là bao nhiêu?
Giải:
Bán kính đáy hình trụ là: r = C/2π = 30/2.3,14 = 4,78 cm
Thể tích hình trụ: V = Sđáy.h = π.r2.h = 717,44 (cm3)
Đáp số: 717,44 (cm3)
Bài 2: Tính thể tích hình trụ bên dưới, biết: r = 3 cm, AC = 5 cm.
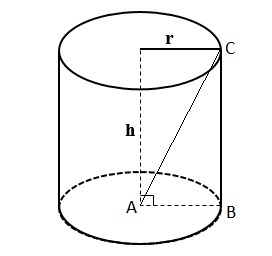
Giải:
– Tính chiều cao hình trụ:
Xét tam giác vuông ABC, ta có:
AB = r = 3 cm
BC = h
BC2 = AC2 – AB2 = 52 – 32 = 16
=> BC = 4 cm
=> h = 4 cm
– Tính diện tích đáy hình trụ:
Sđáy = π.r2 = 28,26 (cm2)
=> Thể tích hình trụ ở trên là: V = Sđáy.h = 28,26.4 = 113,04 (cm3)
Như vậy các bạn cần phải nhớ định nghĩa về hình trụ và công thức tính thể tích hình trụ. Những bài toán dù phức liên quan đến thể tích hình trụ đều có thể được giải quyết qua công thức này. Điều quan trọng là sự linh hoạt trong tư duy của bạn tới đâu mà thôi. Làm nhiều bài tập sẽ giúp bạn thuộc công thức và rèn luyện kỹ năng phân tích bài toán hình học về hình trụ. Chúc các bạn học tốt môn toán nói chung cũng như phần hình học nói riêng nhé!
Từ khóa » Chu Vi đáy Khối Trụ
-
Tính Thể Tích Của Khối Trụ Biết Chu Vi đáy Của Hình Trụ đó Bằng 6pi ...
-
Cho Hình Trụ Có Chu Vi đáy Là (10pi ) Và Chiều Cao (h = 11 ) .
-
Tính Thể Tích (V ) Của Khối Trụ Có Chu Vi đáy Là (2pi , ) Chiều
-
Một Hình Trụ Có Chiều Cao Bằng 3, Chu Vi đáy Bằng 4 . Tính Thể Tích ...
-
Công Thức Tính Chu Vi Diện Tích Và Thể Tích Của Hình Trụ Rõ Ràng Nhất
-
Tính Thể Tích Của Khối Trụ Biết Chu Vi đáy Của Hình Trụ đó Bằng 6π (cm ...
-
Tính Thể Tích V Của Khối Trụ Có Chu Vi đáy Là 2pi, Chiều Cao - Khóa Học
-
Thể Tích Của Khối Trụ Có Chu Vi đáy Bằng 4.pi.a...
-
Một Hình Trụ Có Chiều Cao Bằng 3, Chu Vi đáy Bằng 4 Pi. Thể Tích...
-
Hướng Dẫn Cách Tính Diện Tích Xung Quanh Hình Trụ Chuẩn Xác 100%
-
Tính Thể Tích Của Khối Trụ Biết Chu Vi đáy Của Hình Trụ đó Bằng
-
Cho Hình Trụ Có Chiều Cao Bằng 5, Chu Vi đáy Bằng \(8\pi \). Tính Thể ...
-
Thể Tích Của Khối Trụ Có Chu Vi đáy Bằng \(4\pi A\) Và độ Dài đường ...