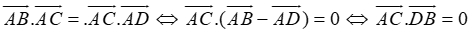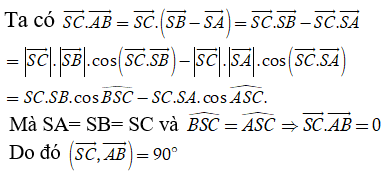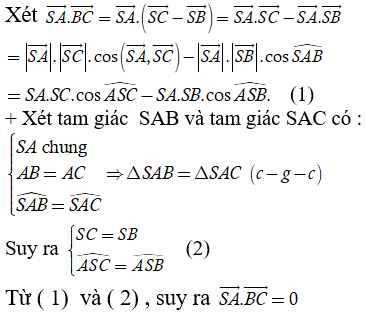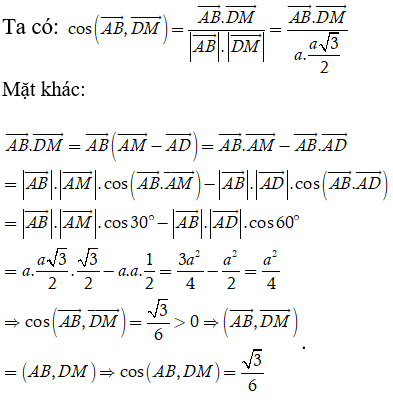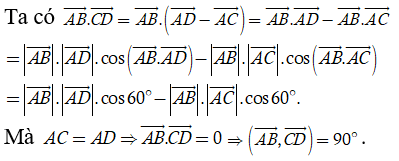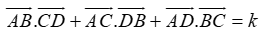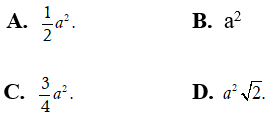Cách Tính Tích Vô Hướng Của Hai Vectơ Hay, Chi Tiết

Cách tính tích vô hướng của hai vectơ hay, chi tiết

A. Phương pháp giải

Trong không gian, cho hai vectơu→vàv→đều khác0→. Tích vô hướng của hai vectơu→vàv→là một số, kí hiệu làu→.v→, được xác định bởi công thức:

Trong trường hợpu→=0→hoặcv→=0→, ta quy ướcu→.v→=0→

B. Ví dụ minh họa

Ví dụ 1:Cho tứ diện ABCD. Chứng minh rằng nếu

thì AB ⊥ CD , AC ⊥ BD, AD ⊥ BC. Điều ngược lại đúng không?

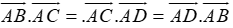
Sau đây là lời giải:

Bước 1:

⇔ AC ⊥ BD

Bước 2: Chứng minh tương tự, từAC→.AD→=AD→.AB→ta đượcAD→⊥BC→vàAB→.AC→=AD→.AB→ta đượcAB→⊥CD→

Bước 3: Ngược lại đúng, vì quá trình chứng minh ở bước 1 và 2 là quá trình biến đổi tương đương

Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?

A. Sai ở bước 3

B. Đúng

C. Sai ở bước 2

D. Sai ở bước 1

Hướng dẫn giải

Chọn B

Bài giải đúng

Ví dụ 2:Cho hình chóp S.ABC có SA = SB = SC và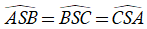. Hãy xác định góc giữa cặp vectơSC→vàAB→?

A. 120° B. 45° C. 60° D. 90°

Hướng dẫn giải

Chọn D

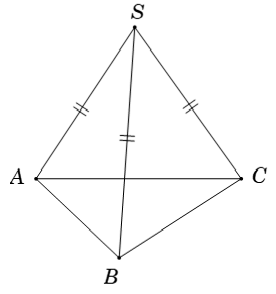
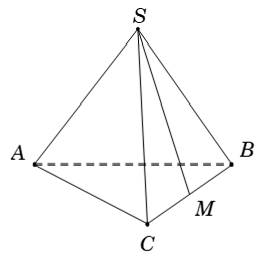
Ví dụ 3:Cho hình chóp S.ABC có SA = SB và CA = CB. Tính số đo của góc giữa hai đường thẳng chéo nhau SC và AB

A. 30° B. 45° C. 60° D. 90°

Hướng dẫn giải

Xét:

Vậy SC và AB vuông góc với nhau

Chọn D

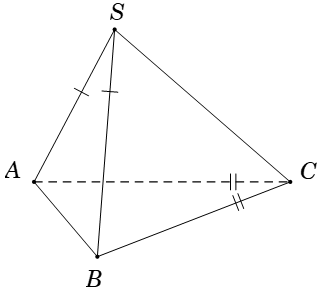
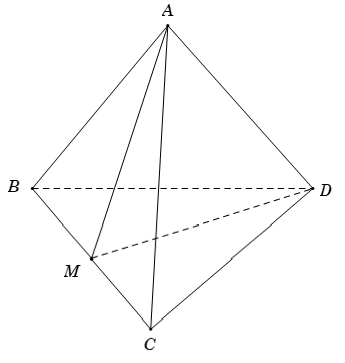
Ví dụ 4:Cho hình chóp S.ABC có AB = AC và ∠SAC = ∠SAB . Tính số đo của góc giữa hai đường thẳng chéo nhau SA và BC

A. 30° B. 45° C. 60° D. 90°

Hướng dẫn giải

Vậy SA ⊥ BC

Chọn D

Ví dụ 5:Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Khi đó cos(AB; DM) bằng :

Hướng dẫn giải

Giả sử cạnh của tứ diện là a.

Tam giác BCD đều ⇒ DM = (a√3)/2.

Tam giác ABC đều ⇒ AM = (a√3)/2.

Chọn B.

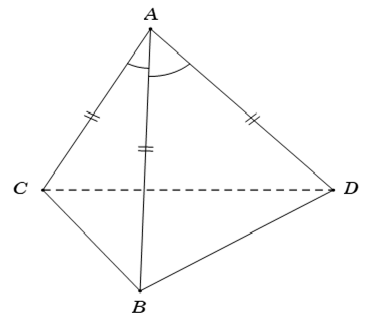
Ví dụ 6:Cho tứ diện ABCD có AB = AC = AD và ∠BAC = ∠BAD = 60° . Hãy xác định góc giữa cặp vectơAB→vàCD→?

A. 60° B. 45° C . 120° D. 90°

Hướng dẫn giải

Chọn D

C. Bài tập vận dụng

Câu 1:Cho hình chóp S. ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo của góc (MN ; SC) bằng

A. 45° B. 30° C. 90° D.60°

Câu 2:Cho hình lập phương ABCD.EFGH có cạnh bằng a. TínhAB→.EG→

Câu 3:Cho tứ diện ABCD. Tìm giá trị của k thích hợp thỏa mãn:

A. k = 1 B. k = 2 C. k = 0 D. k = 4

Câu 4:Cho tứ diện ABCD đều cạnh bằng a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Góc giữa AO và CD bằng bao nhiêu ?

A. 0° B. 30° C. 90° D. 60°

Câu 5:Cho hai vectơa→vàb→thỏa mãn: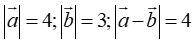. Gọi α là góc giữa hai vectơa→vàb→. Chọn khẳng định đúng?

Câu 6:Trong không gian cho tam giác ABC có trọng tâm G. Chọn hệ thức đúng?

A. AB2+ AC2+ BC2= 2.(GA2+ GB2+ GC2)

B. AB2+ AC2+ BC2= GA2+ GB2+ GC2

C. AB2+ AC2+ BC2= 4.(GA2+ GB2+ GC2)

D. AB2+ AC2+ BC2= 3.(GA2+ GB2+ GC2)

Câu 7:Cho tứ diện ABCD có AC = (3/2)AD, ∠CAB = ∠DAB = 60°, CD = AD. Gọi α là góc giữa AB và CD. Chọn khẳng định đúng?

A. cosα = (3/4) B. α = 60° C. α = 30° D. cosα = 1/4

Câu 8:Cho tứ diện ABCD có AB = AC = AD và ∠BAC = ∠BAD = 60°, ∠CAD = 90°. Gọi I và J lần lượt là trung điểm của AB và CD . Hãy xác định góc giữa cặp vectơAB→vàIJ→?

A. 120° B. 90° C. 60° D. 45°

Câu 9:Cho hình lập phương ABCD.A1B1C1D1 có cạnh a. Gọi M là trung điểm AD. Giá trịB1M→.BD1→là:

Câu 10:Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng:

A. 60° B. 30° C. 90° D. 45°