Cách Xác định Tập Hợp, Tập Hợp Con, Cách Tìm Số Tập Con Của 1 Tập Hợp

Bài này các em sẽ biết cách xác định tập hợp, tập hợp con, hai tập hợp bằng nhau và cách tìm số tập con của một tập hợp.

• Bài tập về tập hợp con, cách xác định tập hợp, số phần tủ tập con

I. Khái niệm tập hợp

1. Tập hợp và phần tử

- Tập hợp là một khái niệm cơ bản (không định nghĩa) của toán học.

- Tập hợp thường được ký hiệu bằng các chữ cái in hoa như: A, B, C,...,X.Y. Các phần tử của tập hợp được ký hiệu bằng các chữ in thường như: a,b,...x,y. 

- Để chỉ phần tử a thuộc tập A ta viết a ∈ A, ngược lại a ∉ A để chị a không thuộc A. Các phần tử của tập hợp được đặt trong cặp dấu {}.

2. Cách xác định tập hợp

• Có 2 cách:

1- Liệt kê các phần tử: Mỗi phần tử liệt kê một lần, giữa các phần tử có dấu phẩy hoặc dấu chấm phẩy ngăn cách. Nếu số lượng phần tử nhiều có thể dùng dấu ba chấm.

* Ví dụ: A = {2; 4; 6; 8}

 B = {0; 1; 2; 3;...; 10}

2- Chỉ rõ tính chất đặc trưng của các phần tử trong tập hợp, tính chất này được viết sau dấu gạch đứng

* Ví dụ: A = {x ∈ N | x chẵn và x < 10}

 B = { x ∈ R | x2 - x - 6 = 0}

- Để minh họa một tập hợp người ta dùng một đường cong khép kín giới hạn một phần mặt phẳng. Các điểm thuộc phần mặt phẳng này chỉ các phần tử của tập hợp ấy. 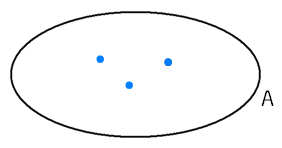3. Tập hợp rỗng

- Một tập hợp không có phần tử nào được gọi là tập hợp rỗng, kí hiệu ∅.

* Ví dụ: A = {  x ∈ R | x2 - x + 1 = 0}

Phương trình x2 - x + 1 = 0 không có nghiệm, nên tập hợp các nghiệm của phương trình này là tập hợp rỗng.

II. Tập hợp con

• Tập hợp con

Nếu tập A là con của tập B, ký hiệu: A ⊂ B hoặc B ⊃ A

Khi: A ⊂ B ⇔ ∀x (x ∈ A ⇒ x ∈ B).

* Ví dụ: A = {2;4;6;8}

 B = {1;2;3;...;10}

• Các tính chất của tập hợp

 A ⊂ A với mọi tập hợp A

 Nếu A ⊂ B và B ⊂ C thì A ⊂ C

 ∅ ⊂ A với mọi tập hợp A

• Cách tìm số tập con của 1 tập hợp (đọc thêm)

+ Cho tập hợp A có n phần tử. Số tập con của A sẽ là: 2n

(có thể chứng minh điều này bằng quy nạp toán học)

* Ví dụ: Cho tập hợp A = {1;2;3} khi đó số tập con của A là 23 = 8. Ta có thể liệt kê các tập con cụ thể như sau:

 ∅; {1}; {2}; {3}; {1;2}; {1;3}; {2;3}; {1;2;3}

+ Cho tập hợp A có n phần tử, khi đó số tập con có k phần tử của tập A là:

 

* Ví dụ: Cho A = {1;2;3;4} khi đó số tập con có 3 phần tử của A là:

  

4. Tập hợp bằng nhau

- Hai tập hợp A và B bằng nhau, kí hiệu A = B, nếu tất cả các phần tử của chúng như nhau.

 A = B ⇔ A ⊂ B và B ⊂ A hay A = B ⇔ ∀x (x ∈ A ⇔ x ∈ B)