Câu III.1, III.2, III.3, III.4 Trang 54 Sách Bài Tập (SBT) Toán Lớp 7 Tập 2

Câu III.1 trang 54 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Chứng minh rằng trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ một đỉnh.

Giải

Vì đường cao và đường trung tuyến xuất phát từ cùng một đỉnh lần lươt là đường vuông góc và đường xiên kẻ từ cùng một điểm đến cùng một đường thẳng nên ta có điều phải chứng minh.

Câu III.2 trang 54 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC có hai đường trung tuyến AD, BE vuông góc với nhau. Chứng minh rằng BC < 2AC.

Giải

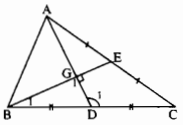
BC < 2AC nếu \({1 \over 2}BC = C{\rm{D < AC}}\)

Xét hai tam giác ADC có \(\widehat {{D_1}} = \widehat {{G_1}} + \widehat {{B_1}}\). Theo giả thiết \(\widehat {{G_1}} = 90^\circ \) nên \(\widehat {{D_1}}\) là góc tù.

Cạnh AC đối diện với góc \({{\rm{D}}_1}\) nên là cạnh lớn nhất, vậy AC > DC hay 2AC > 2DC = BC.

Câu III.3 trang 54Sách Bài Tập (SBT) Toán lớp 7 tập 2

Ba đường phân giác AD, BE, CF của tam giác ABC quy đồng tại O. Kẻ đường vuông góc OG đến BC. Chứng minh rằng \(\widehat {BOG} = \widehat {CO{\rm{D}}}\).

Giải

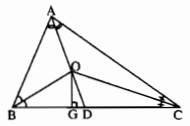
Để chứng minh \(\widehat {BOG} = \widehat {CO{\rm{D}}}\), ta chứng minh \(\widehat {BO{\rm{D}}} = \widehat {GOC}\).

Xét tam giác OAB, ta có

\(\widehat {BO{\rm{D}}} = {1 \over 2}\left( {\widehat A + \widehat B} \right) = {1 \over 2}\left( {180^\circ  - \widehat C} \right)\)                             (1)

Xét tam giác vuông OCG ta có:

\(\widehat {GOC} = 90^\circ  - {1 \over 2}\widehat C = {1 \over 2}\left( {180^\circ  - \widehat C} \right)\)                (2)

Từ (1) và (2) suy ra \(\widehat {BO{\rm{D}}} = \widehat {GOC}\). Vậy \(\widehat {BOG} = \widehat {CO{\rm{D}}}\).

Câu III.4 trang 54Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho tam giác ABC cân tại B có \(\widehat B = 112^\circ \). Kẻ đường cao AH và đường phân giác AD của tam giác đó. Tính các góc của tam giác AHD.

Giải

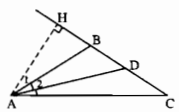
Xét tam giác vuông AHB. Ta có:

\(\widehat {ABH} = 180^\circ  - 112^\circ  = 68^\circ \)

\(\widehat {{A_1}} = 90^\circ  - \widehat {ABH} = 90^\circ  - 68^\circ  = 22^\circ \)

Tam giác ABC cân tại B có \(\widehat B = 112^\circ \) nên  

$$\widehat {BAC} = \left( {180^\circ  - 112^\circ } \right):2 = 34^\circ $$

Do đó \(\widehat {{A_2}} = 34^\circ :2 = 17^\circ \).Từ đó 

\(\widehat {HA{\rm{D}}} = \widehat {{A_1}} + \widehat {{A_2}} = 22^\circ  + 17^\circ  = 39^\circ \)

\(\widehat {H{\rm{D}}A} = 90^\circ  - \widehat {HA{\rm{D}}} = 90^\circ  - 39^\circ  = 51^\circ \)

Sachbaitap.com