Chi-Square Test Of Independence - Statistics Solutions

Trang chủ » H0 Chi2 » Chi-Square Test Of Independence - Statistics Solutions

Có thể bạn quan tâm

The Chi-Square test of independence is used to determine if there is a significant relationship between two nominal (categorical) variables. First, you can compare the frequency of each category for one nominal variable across the categories of the second nominal variable. Then, this comparison helps to identify any potential relationship between the two variables. Also, they can display the data in a contingency table, where each row represents a category for one variable and each column represents a category for the other variable.

For example, say a researcher wants to examine the relationship between gender (male vs. female) and empathy (high vs. low). The chi-square test of independence can be used to examine this relationship. Specifically, the null hypothesis for this test states that there is no relationship between gender and empathy. The alternative hypothesis is that there is a relationship between gender and empathy (e.g. there are more high-empathy females than high-empathy males).

Calculate Chi Square Statistic by Hand

First we have to calculate the expected value of the two nominal variables. We can calculate the expected value of the two nominal variables by using this formula:

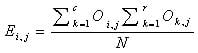
Where

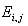= expected value

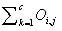= Sum of the ith column

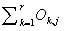= Sum of the kth row

N = total number

After calculating the expected value, we will apply the following formula to calculate the value of the Chi-Square test of Independence:

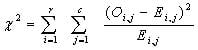
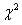= Chi-Square test of Independence 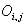= Observed value of two nominal variables 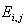= Expected value of two nominal variables

One can calculate the degrees of freedom using the following formula:DF = (r-1)(c-1)WhereDF = Degree of freedomr = number of rowsc = number of columns

Từ khóa » H0 Chi2