Chinh Phục Hằng đẳng Thức Bậc 3 Từ Cơ Bản đến Nâng Cao 2021
Có thể bạn quan tâm
Hằng đẳng thức bậc 3 là một trong những bí quyết “khó xơi” trong toán học sơ cấp. bài viết “Chinh phục hằng đẳng thức bậc 3 từ cơ bản đến nâng cao 2021″ do TopUni.vn biên soạn sẽ giúp các bạn nắm vững thêm kiến thức qua đó áp dụng vào giải nhanh các bài toán hình học và đại số một cách an toàn nhất.
Hằng đẳng thức bậc 3 cơ bản

1. Bình phương của một tổng
Với A, B là các biểu thức tùy ý, ta có: ( A + B )2 = A2 + 2AB + B2.
Ví dụ:
a) Tính ( a + 3 )2. b) Viết biểu thức x2+ 4x + 4 dưới dạng bình phương của một tổng.
Hướng dẫn:
a) Ta có: ( a + 3 )2= a2+ 2.a.3 + 32 = a2 + 6a + 9. b) Ta có x2+ 4x + 4 = x2+ 2.x.2 + 22 = ( x + 2 )2.
2. Bình phương của một hiệu
Với A, B là các biểu thức tùy ý, ta có: ( A – B )2 = A2 – 2AB + B2.
 3. Hiệu hai bình phương
3. Hiệu hai bình phương
Với A, B là các biểu thức tùy ý, ta có: A2 – B2 = ( A – B )( A + B ).

4. Lập phương của một tổng
Với A, B là các biểu thức tùy ý, ta có: ( A + B )3 = A3 + 3A2B + 3AB2 + B3.

5. Lập phương của một hiệu.
Với A, B là các biểu thức tùy ý, ta có: ( A – B )3 = A3 – 3A2B + 3AB2 – B3.
Ví dụ :
a) Tính ( 2x – 1 )3. b) Viết biểu thức x3– 3x2y + 3xy2– y3 dưới dạng lập phương của một hiệu.
Hướng dẫn:
a) Ta có: ( 2x – 1 )3
= ( 2x )3 – 3.( 2x )2.1 + 3( 2x ).12 – 13
= 8x3 – 12x2 + 6x – 1
b) Ta có : x3– 3x2y + 3xy2– y3
= ( x )3 – 3.x2.y + 3.x. Y2 – y3
= ( x – y )3
6. Tổng hai lập phương
Với A, B là các biểu thức tùy ý, ta có: A3 + B3 = ( A + B )( A2 – AB + B2 ).
Chú ý: Ta quy ước A2 – AB + B2 là bình phương thiếu của hiệu A – B.
Ví dụ:
a) Tính 33+ 43. b) Viết biểu thức ( x + 1 )( x2– x + 1 ) dưới dạng tổng hai lập phương.
Hướng dẫn:
a) Ta có: 33+ 43= ( 3 + 4 )( 32 – 3.4 + 42 ) = 7.13 = 91. b) Ta có: ( x + 1 )( x2– x + 1 ) = x3+ 13 = x3 + 1.
7. Hiệu hai lập phương
Với A, B là các biểu thức tùy ý, ta có: A3 – B3 = ( A – B )( A2 + AB + B2 ).
Chú ý: Ta quy ước A2 + AB + B2 là bình phương thiếu của tổng A + B.
Ví dụ:
a) Tính 63– 43. b) Viết biểu thức ( x – 2y )( x2+ 2xy + 4y2) dưới dạng hiệu hai lập phương
Hướng dẫn:
a) Ta có: 63– 43= ( 6 – 4 )( 62 + 6.4 + 42 ) = 2.76 = 152. b) Ta có : ( x – 2y )( x2+ 2xy + 4y2) = ( x )3 – ( 2y )3 = x3 – 8y3.
B. Bài tập tự luyện về hằng đẳng thức
Bài 1.Tìm x biết
a) ( x – 3 )( x2+ 3x + 9 ) + x( x + 2 )( 2 – x ) = 0. b) ( x + 1 )3– ( x – 1 )3– 6( x – 1 )2 = – 10.
Hướng dẫn:
a) Áp dụng các hằng đẳng thức ( a – b )( a2+ ab + b2) = a3 – b3.
( a – b )( a + b ) = a2 – b2.
Lúc đó ta có ( x – 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 – x ) = 0.
⇔ x3 – 33 + x( 22 – x2 ) = 0 ⇔ x3 – 27 + x( 4 – x2 ) = 0
⇔ x3 – x3 + 4x – 27 = 0
⇔ 4x – 27 = 0
Vậy x= 27/4.
b) Dùng hằng đẳng thức ( a – b )3= a3– 3a2b + 3ab2 – b3
( a + b )3 = a3 + 3a2b + 3ab2 + b3
( a – b )2 = a2 – 2ab + b2
Lúc đó ta có: ( x + 1 )3 – ( x – 1 )3 – 6( x – 1 )2 = – 10.
⇔ ( x3 + 3x2 + 3x + 1 ) – ( x3 – 3x2 + 3x – 1 ) – 6( x2 – 2x + 1 ) = – 10
⇔ 6x2 + 2 – 6x2 + 12x – 6 = – 10
⇔ 12x = – 6
Vậy x= -1/2
Bài 2: Rút gọn biểu thức
A = (x + 2y ).(x – 2y) – (x – 2y)2
- 2x2+ 4xy B. – 8Y2+ 4xy
- – 8y2 D. – 6Y2+ 2xy
Hướng dẫn
Ta có: A = (x + 2y ). (X – 2y) – (x – 2y)2
A = x2 – (2y)2 – [x2 – 2.x.2y +(2y)2 ]
A = x2 – 4y2 – x2 + 4xy – 4y22
A = -8y2 + 4xy
- Hãy nhớ nó nhé

Phát biểu hằng đẳng thức bậc ba đáng nhớ bằng lời
1. Bình phương của 1 tổng sẽ bằng bình phương của số thứ 1 cộng với hai lần tích của số thứ nhất với số thứ 2 cộng bình phương số thứ hai
2. Bình phương của 1 hiệu sẽ bằng bình phương của số thứ 1 trừ 2 lần tích số thứ nhất với số thứ 2 cộng với bình phương số thứ hai.
3. Hiệu của 2 bình phương sẽ bằng tích của tổng 2 số với hiệu 2 số.
4. Lập phương của 1 tổng sẽ bằng với lập phương số thứ 1 + 3 lần tích bình phương số thứ 1 với số thứ 2 + 3 lần tích số thứ 1 với bình phương số thứ 2 + lập phương số thứ 2.
5. Lập phương của 1 tổng sẽ bằng với lập phương số thứ 1 -3 lần tích bình phương số thứ 1 với số thứ hai + 3 lần tích số thứ 1 với bình phương số thứ 2 – lập phương số thứ hai.
6. Tổng hai lập phương sẽ bằng tích giữa tổng 2 số với bình phương thiếu của 1 hiệu.
7. Hiệu của 2 lập phương sẽ bằng với tích giữa hiệu hai số với bình phương thiếu của 1 tổng.
Hằng đẳng thức mở rộng với hàm bậc 3
- a3 + b3 = (a + b)3 – 3ab(a + b)
- a3 – b3 = (a – b)3 + 3ab(a – b)
- (a + b + c)3 = a3 + b3 + c3 + 3(a + b)(b + c)(a + c)
- a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ac)
- (a – b)3 + (b – c)3 + (c – a)3 = 3(a – b)(b – c)(c – a)
- (a + b)(b + c)(c + a) – 8abc = a(b – c)2 + b(c – a)2 + c(a – b)2
- (a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) – abc
Hằng đẳng thức dạng tổng quát
- an + bn = (a + b)(an-1 – an-2 b + an-3 b2 – an-4 b3 + … + a2bn-3 – abn-2 + bn-1)
- an – bn = (a – b)(an-1 + an-2 b + an-3 b2 + an-4 b3 + … + a2bn-3 + abn-2 + bn-1)
- Với n là số lẻ thuộc N (tập hợp số tự nhiên)
Nhị thức Newton
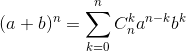
Với a,b thuộc tập hợp số thực (R), n thuộc tập hợp số tự nhiên dương (N*)
Trong những hằng đẳng thức này, 1 bên dấu bằng là tổng hoặc hiệu và bên gọi lại là tích hoặc lũy thừa. Những đẳng thức này luôn được sử dụng thường xuyên trong các bài toán liên quan đến giải phương trình, nhân chia đa thức, biến đổi biểu thức tại từ cấp 2 đến cấp 3 và 7 hằng đẳng thức đáng nhớ được in trong sách giáo khoa và được in rất nhiều trong bìa sau của vở viết cấp II hoặc cấp III của học sinh.
Mẹo nhớ các hằng đẳng thức bậc 3
Nếu để ý, ta có thể nhận ra rằng, các hằng đẳng thức: Bình phương của 1 tổng và 1 hiệu; Lập phương của 1 tổng và 1 hiệu; Tổng và Hiệu 2 lập phương đều khá tương tự nhau, chỉ khác nhau ở dấu. Vì vậy điều cần lưu ý ở Nó là ghi nhớ dấu của chúng, từ đấy ta có khả năng học thuộc một cách chính xác và không bị nhầm lẫn.
So với hằng đẳng thức Lập phương của 1 hiệu và Tổng 2 lập phương thì cần chú ý đấy chính là:
- “ Hiệu các lập phương bằng tích của hiệu hai số và bình phương thiếu của một tổng”
- “Tổng các lập phương bằng tích của tổng hai số và bình phương thiếu của một hiệu”
Kết luận
Những hằng đẳng thức đáng nhớ trên cực kì thiết yếu tủ kiến thức của mỗi học sinh . Thế nên các bạn hãy nghiên cứu và ghi nhớ nó để áp dụng vào trong kì thi sắp đến. Nếu như bạn thấy bài viết “Chinh phục hằng đẳng thức bậc 3 từ cơ bản đến nâng cao 2021″ do TopUni.vn soạn thảo hữu ích, đừng bao giờ quên sẻ chia và để lại bình luận để tụi mình biết nhé.
Từ khóa » Giải Hằng đẳng Thức Bậc 3
-
Hằng đẳng Thức Bậc 3 - Phạm Vũ Dương Sơn
-
Hằng Đẳng Thức Đáng Nhớ - Kiến Thức Quan Trọng Cần Nhớ
-
Các Hằng đẳng Thức Mở Rộng Cơ Bản Và Nâng Cao
-
7 Hằng đẳng Thức đáng Nhớ Cơ Bản Và Mở Rộng - Trường Quốc Học
-
7 Hằng Đẳng Thức Đáng Nhớ Và Hệ Quả Lớp 8
-
Các Hằng Đẳng Thức Mở Rộng Cơ Bản Và Nâng Cao
-
7 Hằng đẳng Thức đáng Nhớ Cơ Bản Và Mở Rộng - DINHNGHIA.VN
-
Các Hằng Đẳng Thức Mở Rộng Cơ Bản Và Nâng Cao
-
7 Hằng đẳng Thức đáng Nhớ Cơ Bản Và Mở Rộng - Wiki Cách Làm
-
[Toán Nâng Cao Lớp 8] - Hằng đẳng Thức Bậc 3 - Thầy Nguyễn Hùng ...
-
Hằng đẳng Thức Bậc 3 Mở Rộng
-
Hằng đẳng Thức Căn Bậc Ba | Toán Lớp 9
-
Hằng Đẳng Thức Bậc 3