Cho Ba Vectơ A Vectơ B Vectơ C Không đồng Phẳng. Xét Các Vectơ X...

× Đăng nhập Facebook Google ×

CHỌN BỘ SÁCH BẠN MUỐN XEM

Hãy chọn chính xác nhé!

Trang chủ Lớp 11 Toán

Câu hỏi:

23/07/2024 15,553

Cho ba vectơ a→,b→,c→ không đồng phẳng. Xét các vectơ x→=2a→+b→;y→=a→-b→-c→,z→=-3a→-2c→. Khẳng định nào dưới đây là đúng ?

A. Ba vectơ x→,y→,z→ đồng phẳng.

Đáp án chính xác

B. Hai vectơ x→,a→ cùng phương.

C. Hai vectơ x→,b→ cùng phương.

D. Ba vectơ x→,y→,z→ đôi một cùng phương

Xem lời giải Xem lý thuyết Câu hỏi trong đề: Trắc nghiệm Véc tơ trong không gian có đáp án Bắt Đầu Thi Thử

Trả lời:

Giải bởi Vietjack

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết

ĐĂNG KÝ VIP

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho tứ diện ABCD. Trên các cạnh AD và BC lần lượt lấy M, N sao cho AM=3MD, BN=3NC. Gọi P, Q lần lượt là trung điểm của AD và BC. Trong các khẳng định sau, khẳng định nào sai?

Xem đáp án » 31/07/2021 9,805

Câu 2:

Cho tứ diện ABCD. Đặt AB→=a→,AC→=b→,AD→=c→, gọi G là trọng tâm của tam giác BCD. Trong các đẳng thức sau, đẳng thức nào đúng?

Xem đáp án » 31/07/2021 7,615

Câu 3:

Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ: MN→=kAD→+BC→

Xem đáp án » 31/07/2021 5,618

Câu 4:

Cho hình tứ diện ABCD, trọng tâm G. Mệnh đề nào sau đây đúng?

Xem đáp án » 28/07/2021 5,028

Câu 5:

Cho tứ diện ABCD và điểm G thỏa mãn GA→+GB→+GC→+GD→=0→ ( G là trọng tâm của tứ diện). Gọi G0 là giao điểm của GA và mp (BCD). Trong các khẳng định sau, khẳng định nào đúng?

Xem đáp án » 31/07/2021 4,483

Câu 6:

Cho hình tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây sai.

Xem đáp án » 31/07/2021 4,040

Câu 7:

Cho ABCD.A1B1C1D1 là hình hộp, trong các khẳng định sau khẳng định sai:

Xem đáp án » 28/07/2021 2,758

Câu 8:

Cho tứ diện ABCD. Trên các cạnh AD,BC lần lượt lấy M,N sao cho AM=3MD;BN=3NC. Gọi P,Q lần lượt là trung điểm của AD,BC. Trong các khẳng định sau, khẳng định nào sai?

Xem đáp án » 31/07/2021 2,714

Câu 9:

Cho hai điểm phân biệt A, B và một điểm O bất kỳ không thuộc đường thẳng AB. Mệnh đề nào sau đây là đúng?

Xem đáp án » 31/07/2021 2,689

Câu 10:

Cho tứ diện đều ABCD, M là trung điểm của cạnh AB và G là trọng tâm cuả tam giác BCD. Đặt AB→=b→,AC→=c→,AD→=d→. Phân tích véc tơ MG→ theo d→,b→,c→

Xem đáp án » 31/07/2021 2,631

Câu 11:

Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi G là điểm thỏa mãn: GS→+GA→+GB→+GC→+GD→=0→. Trong các khẳng định sau, khẳng định nào đúng?

Xem đáp án » 31/07/2021 1,904

Câu 12:

Cho tứ diện ABCD và điểm G thỏa mãn GA→+GB→+GC→+GD→=0→. Gọi O là giao điểm của GA và mặt phẳng (BCD). Trong các khẳng định sau, khẳng định nào đúng?

Xem đáp án » 28/07/2021 1,013

Câu 13:

Trong mặt phẳng (α) cho tứ giác ABCD và một điểm S tùy ý. Mệnh đề nào sau đây đúng?

Xem đáp án » 28/07/2021 932

Câu 14:

Cho tứ diện ABCD. M là điểm trên đoạn AB và MB=2MA. N là điểm trên đường thẳng CD mà CN→=kCD→.Nếu MN→,AD→,BC→ đồng phẳng thì giá trị của k là:

Xem đáp án » 31/07/2021 843 Xem thêm các câu hỏi khác »

LÝ THUYẾT

Mục lục nội dung

Xem thêm

I. Định nghĩa và các phép toán về vecto trong không gian.

Cho đoạn thẳng AB trong không gian. Nếu ta chọn điểm đầu là A, điểm cuối là B ta có một vecto, được kí hiệu là AB→.

1. Định nghĩa.

- Vecto trong không gian là một đoạn thẳng có hướng. Kí hiệu AB→chỉ vecto có điểm đầu là A, điểm cuối là B. Vecto còn được kí hiệu là a→;  b→;  x→;  y→....

- Các khái niệm liên quan đến vecto như giá của vecto, độ dài của vecto, sự cùng phương, cùng hướng của vecto, vecto – không, sự bằng nhau của hai vecto ….được định nghĩa tương tự như trong mặt phẳng.

2. Phép cộng và phép trừ vecto trong không gian,

- Phép cộng và phép trừ của hai vecto trong không gian được định nghĩa tương tự như phép cộng và phép trừ hai vecto trong mặt phẳng.

- Phép cộng vecto trong không gian cũng có các tính chất như phép cộng vecto trong mặt phẳng. Khi thực hiện phép cộng vecto trong không gian ta vẫn có thể áp dụng quy tắc ba điểm, quy tắc hình bình hành như đối với vecto trong hình học phẳng.

Ví dụ 1. Cho tứ diện ABCD. Chứng minh DA→ +​  BC→ =  BA→  +​  DC→

Lời giải:

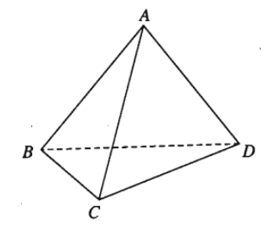
Áp dụng quy tắc ba điểm ta có: DA→  = DC→ + CA→

Ta có: DA→ +​  BC→ = DC→ + CA→   +​  BC→=  DC→ +​  BC→ +​  CA→=  DC→  +​  BA→

( điều phải chứng minh).

II. Điều kiện đồng phẳng của ba vecto.

1. Khái niệm về sự đồng phẳng của ba vecto trong không gian.

Trong không gian cho ba vecto a→; b→ ;  c→  ≠0→. Nếu từ một điểm O bất kì ta vẽ: OA→  = a→; OB→  = b→ ; OC→=  c→  thì có thể xảy ra hai trường hợp:

+ Trường hợp các đường thẳng OA; OB; OC không cùng nằm trong một mặt phẳng, khi đó ta nói rằng ba vecto a→; b→ ;  c→   không đồng phẳng.

+ Trường hợp các đường thẳng OA; OB; OC cùng nằm trong một mặt phẳng thì ta nói rằng ba vecto a→; b→ ;  c→   đồng phẳng.

Trong trường hợp này, giá của các vecto a→; b→ ;  c→   luôn luôn song song với một mặt phẳng.

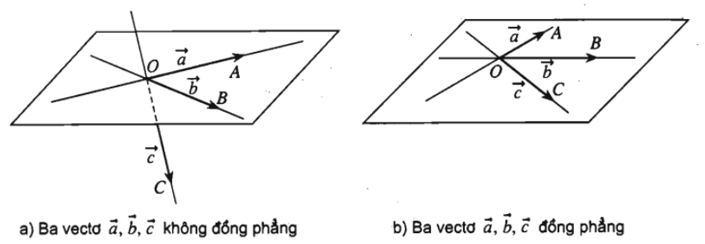
- Chú ý. Việc xác định sự đồng phẳng hoặc không đồng phẳng của ba vecto nói trên không phụ thuộc vào việc chọn điểm O.

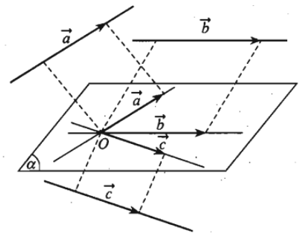
2. Định nghĩa:

Trong không gian ba vecto được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.

Ví dụ 2. Cho hình hộp ABCD.EFGH. Gọi I là tâm hình bình hành ABEF và K là tâm hình bình hành BCGF. Chứng minh BD→,IK→,GF→ đồng phẳng .

Lời giải :

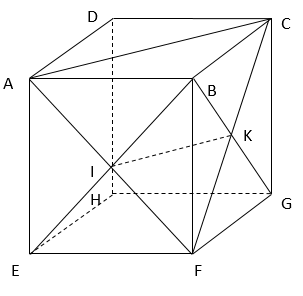
Xét tam giác FAC có I ; K lần lượt là trung điểm của AF và FC nên IK là đường trung bình của tam giác.

⇔ IK// AC nên IK// mp ( ABCD) .

Vì BC// GF nên GF // mp( ABCD)

Ta có :IK//(ABCD)GF//(ABCD)BD⊂(ABCD)  

⇒BD→,IK→,GF→ đồng phẳng.

3. Điều kiện để ba vecto đồng phẳng.

Định lí 1.

Trong không gian cho hai vecto a→; b→không cùng phương và vecto c→. Khi đó, ba vecto a→;  b→;  c→ đồng phẳng khi và chỉ khi có cặp số m; n sao cho c→  =  ma→+ n  b→. Ngoài ra, cặp số m; n là suy nhất.

- Định lí 2.

Trong không gian cho ba vecto không đồng phẳng a→;  b→;  c→. Khi đó, với mọi vecto x→ ta đều tìm được một bộ ba số m, n, p sao cho x→  = ma→+n  b→+p  c→. Ngoài ra, bộ ba số m; n; p là duy nhất.

Ví dụ 3. Cho hình lăng trụ ABC.A’B’C’ gọi M là trung điểm của BB’ . Đặt CA→  = a→;  CB→ = b→; A​A'→=  c→ . Phân tích vecto AM→ theo a→;  b→;  c→.

Lời giải:

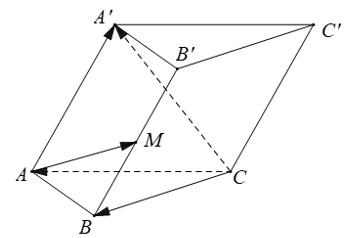
Áp dụng quy tắc 3 điểm và quy tắc hiệu hai vecto ta có :

AM→=AB→+BM→=CB→−CA→+12BB'→ ( BM→  =  12 BB'→ vì M là trung điểm của BB’) .

=b→−a→+12AA'→=b→−a→+12c→.

Hỏi bài

Đề thi liên quan

Xem thêm »

• Trắc nghiệm tổng hơp Toán 11 (có đáp án) 76 đề 30405 lượt thi Thi thử
• Trắc nghiệm Đề thi Toán 11 (có đáp án) 17 đề 10072 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác (có đáp án) 12 đề 6509 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 4: Giới hạn (có đáp án) 7 đề 6202 lượt thi Thi thử
• Trắc nghiệm Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (có đáp án) 8 đề 6184 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 5: Đạo hàm (có đáp án) 11 đề 4856 lượt thi Thi thử
• Trắc nghiệm Toán 11 Bài 2: Phương trình lượng giác cơ bản (có đáp án) 6 đề 4658 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 2: Tổ hợp - Xác suất (có đáp án) 15 đề 4424 lượt thi Thi thử
• Trắc nghiệm Toán 11 Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng (có đáp án) 9 đề 4100 lượt thi Thi thử
• Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác (có đáp án) 6 đề 4053 lượt thi Thi thử

Xem thêm »