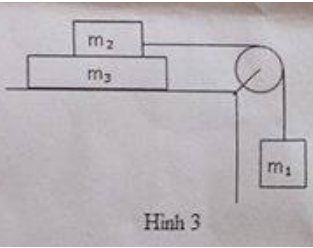
Cho Cơ Hệ Như Hình 3. Ròng Rọc Có Khối Lượng Không đáng Kể, Dây ...

Câu hỏi số 286109: Vận dụng cao

Cho cơ hệ như Hình 3. Ròng rọc có khối lượng không đáng kể, dây nối nhẹ và không dãn, m1 = 2kg, m3 = 1kg; hệ số ma sát trượt giữa m3 và mặt bàn cố định là k = 0,2; hệ số ma sát trượt giữa m2 và m3 là k0 = 0,4; lấy g=10m/s2. Hệ được thả cho chuyển động từ trạng thái nghỉ.

 

a. Hỏi m2 bằng bao nhiêu để nó không trượt trên m3 khi hệ chuyển động?

b. Tính m2 để gia tốc của m3 bằng một nửa gia tốc của m­­­2. Khi đó gia tốc của m2 bằng bao nhiêu?

Quảng cáo

Xem lời giải Câu hỏi:286109 Phương pháp giải

Áp dụng định luật II Niu-tơn

Giải chi tiết

a. Để m2 không trượt trên m3 khi hệ chuyển động thì chúng phải chuyển động cùng gia tốc.

=> a1 = a2 = a3 = a (do dây không giãn)

Áp dụng định luật II Niu -  Tơn vật 1: \(\overrightarrow{{{T}_{1}}}+\overrightarrow{{{P}_{1}}}={{m}_{1}}\overrightarrow{{{a}_{1}}}\) (1)

Chiếu (1) lên hướng chuyển động vật 1: \(-T+{{m}_{1}}g={{m}_{1}}{{a}_{1}}\)=> \({{a}_{1}}=a=\frac{{{m}_{1}}g-T}{{{m}_{1}}}\) (4)

Áp dụng định luật II Niu -  Tơn vật 2: \(\overrightarrow{{{T}_{2}}}+\overrightarrow{{{P}_{2}}}+\overrightarrow{{{Q}_{2}}}+\overrightarrow{{{F}_{ms2}}}={{m}_{2}}\overrightarrow{{{a}_{2}}}\) (2)

Chiếu (2) lên hướng chuyển động vật 2 và lên phương thẳng đứng hướng lên, ta được:\(T-{{F}_{ms2}}={{m}_{2}}{{a}_{2}}\)

Và P2 = Q2=> \({{a}_{2}}=a=\frac{T-{{k}_{0}}{{m}_{2}}g}{{{m}_{2}}}\)  (5)

Áp dụng định luật II Niu -  Tơn vật 3: \(\overrightarrow{{{P}_{3}}}+\overrightarrow{{{Q}_{3}}}+\overrightarrow{n}+\overrightarrow{{{F}_{ms3}}}+\overrightarrow{F_{ms2}^{'}}={{m}_{3}}\overrightarrow{{{a}_{3}}}\) (3)

Chiếu (3) lên hướng chuyển động vật 3 và lên phương thẳng đứng hướng lên, ta được:\(F_{ms2}^{'}-{{F}_{ms3}}={{m}_{3}}{{a}_{3}}\)

Và Q3 = P3 + n = (m2 + m3)g=> \({{a}_{3}}=a=\frac{{{k}_{0}}{{m}_{2}}g-k({{m}_{2}}+{{m}_{3}})g}{{{m}_{3}}}\)   (6)

Từ (4) và (5): \(10-\frac{T}{2}=\frac{T}{{{m}_{2}}}-4\)=> \(T=\frac{28{{m}_{2}}}{2+{{m}_{2}}}\)              (7)

Từ (5), (6) và (7): \(\frac{28}{2+{{m}_{2}}}-4=4{{m}_{2}}-2({{m}_{2}}+1)\)=> \(m_{2}^{2}+3{{m}_{2}}-12=0\)=> \({{m}_{2}}=\frac{\sqrt{57}-3}{2}kg\)

   

b.  a3  = a2/2

=> \(\frac{{{k}_{0}}{{m}_{2}}g-k({{m}_{2}}+{{m}_{3}})g}{{{m}_{3}}}=\frac{T-{{k}_{0}}{{m}_{2}}g}{2{{m}_{2}}}\) => \(\frac{14}{2+{{m}_{2}}}-2=4{{m}_{2}}-2({{m}_{2}}+1)\)=> \({{m}_{2}}=2\sqrt{2}-1kg\)