Cho Hàm Số Y =− Log2 X Có đồ Thị (C). Hàm Số Nào ...

× Đăng nhập Facebook Google ×

CHỌN BỘ SÁCH BẠN MUỐN XEM

Hãy chọn chính xác nhé!

Trang chủ Lớp 12 Toán

Câu hỏi:

23/07/2024 173

Cho hàm sốy=−log2xy=-log2x có đồ thị (C). Hàm số nào sau đây có đồ thị đối xứng (C) qua đường thẳng y = x.

A. y=2x

B. y=21x

C. y=2-x

Đáp án chính xác

D. y=2x2

Xem lời giải Xem lý thuyết Câu hỏi trong đề: Trắc nghiệm Hàm số mũ. Hàm số Logarit có đáp án (Nhận biết) Bắt Đầu Thi Thử

Trả lời:

Giải bởi Vietjack

Trước tiên ta đưa hàm số về dạng chuẩn: y=−log2x=log2−1x=log12xy=-log2x=log2-1x=log12x

Suy ra hàm số cần tìm là: y=(12)x=2−xy=12x=2-x

Đáp án cần chọn là: C.

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết

ĐĂNG KÝ VIP

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho hàm sốy=5xy=5x có đồ thị (C). Hàm số nào sau đây có đồ thị đối xứng với (C) qua đường thẳng y = x.

Xem đáp án » 13/01/2022 1,704

Câu 2:

Hàm số nào sau đây nghịch biến trên khoảng xác định của nó?

Xem đáp án » 13/01/2022 389

Câu 3:

Hàm số nào sau đây đồng biến trên khoảng (0;+∞)

Xem đáp án » 13/01/2022 341

Câu 4:

Chọn khẳng định đúng:

Xem đáp án » 13/01/2022 179

Câu 5:

Chọn mệnh đề đúng:

Xem đáp án » 13/01/2022 175

Câu 6:

Cho hàm sốy=logaxy=logax. Nếu 0<a<1 thì hàm số:

Xem đáp án » 13/01/2022 155

Câu 7:

Chọn mệnh đề đúng:

Xem đáp án » 13/01/2022 137

Câu 8:

Chọn mệnh đề đúng:

Xem đáp án » 13/01/2022 137

Câu 9:

Hàm số y=ax(0<a≠1)y=ax 0<a≠1đồng biến khi nào?

Xem đáp án » 13/01/2022 136

Câu 10:

Choa>0,a≠1a>0, a≠1. Tìm mệnh đề đúng trong các mệnh đề sau:

Xem đáp án » 13/01/2022 136

Câu 11:

Hàm sốy=logax(0<a≠1)y=logax 0<a≠1 xác định trên:

Xem đáp án » 13/01/2022 121

Câu 12:

Gọi (C) là đồ thị hàm sốy=logxy=logx. Tìm khẳng định đúng?

Xem đáp án » 13/01/2022 121

Câu 13:

Chọn khẳng định đúng:

Xem đáp án » 13/01/2022 117

Câu 14:

Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập R?

Xem đáp án » 13/01/2022 114

Câu 15:

Tính đạo hàm của hàm số y=6x

Xem đáp án » 13/01/2022 109 Xem thêm các câu hỏi khác »

LÝ THUYẾT

Mục lục nội dung

Xem thêm

I. Hàm số mũ

1. Định nghĩa.

Cho số thực dương a khác 1.

Hàm số y = ax được gọi là hàm số mũ cơ số a.

Ví dụ 1. Các hàm số y = 2x; y=(12)x;y=(3)x là các hàm số mũ.

2. Đạo hàm của hàm số mũ

Ta thừa nhận công thức: limt→0et-1t=1

– Định lí 1: Hàm số y = ex có đạo hàm tại mọi x và (ex)’ = ex.

– Chú ý: Công thức đạo hàm của hàm hợp đối với hàm số eu ( với u = u(x))

là (eu)’ = u’. eu.

– Định lí 2: Hàm số y = ax ( a > 0; a ≠ 1) có đạo hàm tại mọi x và: (ax)’ = ax. ln a

– Chú ý:Đối với hàm hợp y = au(x) ta có: (au)’ = au. lnu . u’

Ví dụ 2. Hàm số y=  2-x2+ 2⁢x-10 có đạo hàm là:

y'=  2-x2+ 2⁢x-10.(-x2+ 2⁢x-10)'.ln⁡2=  2-x2+ 2⁢x-10.(-2⁢x+2)⁢ln⁡2

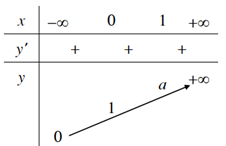
3. Khảo sát hàm số mũ y = ax ( a > 0 và a ≠ 1).

y = ax ; a > 1	y = ax ;0 < a < 1
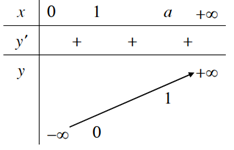
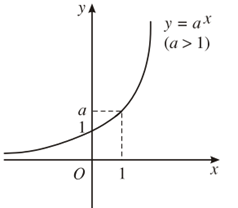
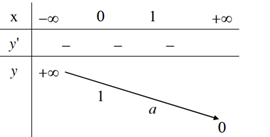
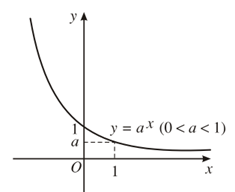
1. Tập xác định: R 2. Sự biến thiên y’ = ax.ln a > 0 với mọi x Giới hạn đặc biệt: limx→ -∞ax=0;limx→+∞ax=⁢ +∞ Tiệm cận: Trục Ox là tiệm cận ngang. 3. Bảng biến thiên: 4. Đồ thị	1. Tập xác định: R 2. Sự biến thiên y’ = ax.ln a < 0 với mọi x Giới hạn đặc biệt: limx→ -∞ax= +∞;limx→⁢ +∞ax=0 Tiệm cận: Trục Ox là tiệm cận ngang. 3. Bảng biến thiên: 4. Đồ thị

Bảng tóm tắt các tính chất của hàm số mũ y = ax ( a > 0; a ≠ 1).

Tập xác định	(-∞;+∞)
Đạo hàm	y’ = ax. lna
Chiều biến thiên	a > 1: Hàm số luôn đồng biến. 0 < a < 1: Hàm số luôn nghịch biến
Tiệm cận	Trục Ox là tiệm cận ngang
Đồ thị	Đi qua các điểm (0; 1) và (1; a), nằm phía trên trục hoành (y = ax > 0 ∀x∈⁢R).

II. Hàm số logarit

1. Định nghĩa.

Cho số thực dương a khác 1.

Hàm số y = logax được gọi là hàm số logarit cơ số a.

Ví dụ 3. Các hàm số y = log5 x; y=log23⁡x;y=log3⁡x; y = ln x là các hàm số logarit với cơ số lần lượt là 5;23;3 và e.

2. Đạo hàm của hàm số logarit

– Định lí 3. Hàm số y = loga x (a > 0; a ≠ 1) có đạo hàm tại mọi x > 0 và (loga⁡x)'=1x⁢ln⁡a

– Đặc biệt: (ln⁡x)'=1x.

– Chú ý:

Đối với hàm hợp y = logau(x); ta có: (loga⁡u)'=u'u⁢ln⁡a

– Ví dụ 4. Hàm số y = log4 (x2 + 2x – 7) có đạo hàm là:

(log4⁡(x2+  2⁢x-7))'=(x2+2⁢x-7)'(x2+2⁢x-7)⁢ln⁡4=2⁢x+ 2(x2+2⁢x-7)⁢ln⁡4.

3. Khảo sát hàm số logarit y = loga x ( a > 0; a ≠ 1).

y = loga x;a >1	y = logax ; 0 < a < 1
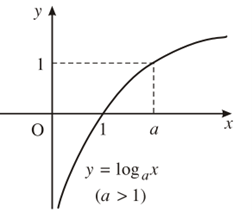
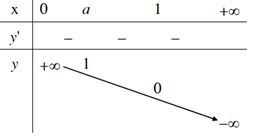
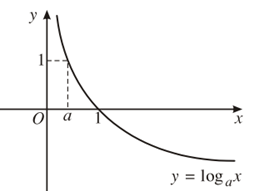
1. Tập xác định: (0;+∞) 2. Sự biến thiên y'=1x⁢ln⁡a>  0;∀x> 0 Giới hạn đặc biệt: limx→0+loga⁡x=-∞;,limx→⁢ +∞logax=+∞. Tiệm cận:Trục Oy là tiệm cận đứng. 3. Bảng biến thiên 4. Đồ thị	1. Tập xác định: (0;+∞) 2. Sự biến thiên y'=1x⁢ln⁡a<   0;∀x> 0 Giới hạn đặc biệt: limx→0+loga⁡x=+∞;,limx→⁢ +∞logax=-∞. Tiệm cận:Trục Oy là tiệm cận đứng. 3. Bảng biến thiên 4. Đồ thị

Bảng tóm tắt các tính chất của hàm số y = logax (a > 0;a ≠ 1 ).

Tập xác định	(0;+∞)
Đạo hàm	y'=1x⁢ln⁡a
Chiều biến thiên	a > 1: hàm số luôn đồng biến 0 < a< 1: hàm số luôn nghịch biến
Tiệm cận	Trục Oy là tiệm cận đứng
Đồ thị	Đi qua các điểm (1; 0) và (a; 1); nằm phía bên phải trục tung

Nhận xét:

Đồ thị của các hàm số y = ax và y = loga x ( a > 0; a ≠ 1) đối xứng với nhau qua đường thẳng y = x.

Bảng đạo hàm của các hàm số lũy thừa, mũ, logarit.

Hàm sơ cấp	Hàm hợp
(xα)'=αxα⁢⁢ -1{(1x)'=-1x2⁢(x)'=12⁢x	(uα)'=αuα⁢⁢ -1.u'{(1u)'=-u'u2⁢(u)'=u'2⁢u
( ex)’ = ex ( ax)’ =ax. ln a	( eu)’ = eu. u’ ( au)’ =au. ln a. u’
(ln⁡|x|)'=1x⁢(loga⁡|x|)'=1x⁢ln⁡a	(ln⁡|u|)'=u'u⁢(loga⁡|u|)'=u'u⁢ln⁡a

Hỏi bài

Đề thi liên quan

Xem thêm »

• 250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số 10 đề 9075 lượt thi Thi thử
• Bài tập về Tính đơn điệu của hàm số có lời giải 3 đề 7730 lượt thi Thi thử
• Trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao 11 đề 7217 lượt thi Thi thử
• Bài tập tắc nghiệm ứng dụng đạo hàm - Toán 12 có đáp án 7 đề 5991 lượt thi Thi thử
• 150 câu trắc nghiệm Nguyên hàm - Tích phân cơ bản (có đáp án) 6 đề 4990 lượt thi Thi thử
• 200 câu trắc nghiệm Phương pháp tọa độ trong không gian NC (có đáp án) 9 đề 4662 lượt thi Thi thử
• Bài tập Cực trị hàm số cơ bản, nâng cao có lời giải 5 đề 4331 lượt thi Thi thử
• 70 câu trắc nghiệm Khối đa diện cơ bản 6 đề 3821 lượt thi Thi thử
• 200 câu trắc nghiệm Phương pháp tọa độ trong không gian (có đáp án) 6 đề 3786 lượt thi Thi thử
• Trắc nghiệm Ôn tập Toán 12 Chương 1 có đáp án 3 đề 3778 lượt thi Thi thử

Xem thêm »