Cho Hàm Số (y = Sin s X - Sin 2x ). Giá Trị Của ((y^(( (10

Một sản phẩm của Tuyensinh247.comCho hàm số (y = sin 3x.cos x - sin 2x ). Giá trị của ((y^(( (10) )))( ((pi )(3)) ) ) gần nhất với số nào dưới đây?Câu 46163 Vận dụng cao

Cho hàm số \(y = \sin 3x.\cos x - \sin 2x\). Giá trị của \({y^{\left( {10} \right)}}\left( {\dfrac{\pi }{3}} \right)\) gần nhất với số nào dưới đây?

Đáp án đúng: d

Phương pháp giải

- Thu gọn hàm số đã cho về hàm số lượng giác cơ bản.

- Sử dụng công thức đạo hàm cấp cao \({\left( {\sin ax} \right)^{\left( n \right)}} = {\left( { - 1} \right)^{n - 1}}{a^n}\sin \left( {\dfrac{{n\pi }}{2} - ax} \right)\)

Xem lời giải

Lời giải của GV Vungoi.vn

Ta có \(y = \sin 3x.\cos x - \sin 2x\)\( = \dfrac{1}{2}\left( {\sin 4x + \sin 2x} \right) - \sin 2x\)\( = \dfrac{1}{2}\left( {\sin 4x - \sin 2x} \right)\)

Mặt khác theo quy nạp ta chứng minh được \({\left( {\sin ax} \right)^{\left( n \right)}} = {\left( { - 1} \right)^{n - 1}}{a^n}\sin \left( {\dfrac{{n\pi }}{2} - ax} \right)\)

Do đó \({y^{\left( {10} \right)}}\left( x \right) = \dfrac{1}{2}\left( {{{\left( { - 1} \right)}^9}{4^{10}}.\sin \left( {5\pi - 4x} \right) - {{\left( { - 1} \right)}^9}{{.2}^{10}}.\sin \left( {5\pi - 2x} \right)} \right)\)

\( = \dfrac{1}{2}\left( { - {4^{10}}.\sin 4x + {2^{10}}\sin 2x} \right)\)

\( \Rightarrow \) \({y^{\left( {10} \right)}}\left( {\dfrac{\pi }{3}} \right)\)\( \approx 454490.13\)

Đáp án cần chọn là: d

...

Bài tập có liên quan

Tổng hợp câu hay và khó chương 5 - Phần 1 Luyện Ngay

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi liên quan

Cho hàm số \(y = {x^3} + 3{x^2}\) có đồ thị \(\left( C \right)\) và điểm \(M\left( {m;0} \right)\) sao cho từ \(M\) vẽ được ba tiếp tuyến đến đồ thị \(\left( C \right)\), trong đó có hai tiếp tuyến vuông góc với nhau. Khi đó khẳng định nào sau đây đúng.

Cho hàm số \(y = f\left( x \right)\) xác định và có đạo hàm trên \(\mathbb{R}\) thỏa mãn \({\left[ {f\left( {2x + 1} \right)} \right]^2} + {\left[ {f\left( {1 - x} \right)} \right]^3} = x\). Viết phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ bằng \(1\).

Cho hàm số \(y = \sin 3x.\cos x - \sin 2x\). Giá trị của \({y^{\left( {10} \right)}}\left( {\dfrac{\pi }{3}} \right)\) gần nhất với số nào dưới đây?

Cho hàm số \(y = \sqrt {1 + 3x - {x^2}} \). Khẳng định nào dưới đây đúng?

Cho hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{a\sqrt x }&{khi}&{0 < x < {x_0}}\\{{x^2} + 12}&{khi}&{x \ge {x_0}}\end{array}} \right.$. Biết rằng ta luôn tìm được một số dương ${x_0}$ và một số thực $a$ để hàm số $f$ có đạo hàm liên tục trên khoảng $\left( {0; + \infty } \right)$. Tính giá trị $S = {x_0} + a$.

Cho hàm số \(y = {x^3} + 3m{x^2} + \left( {m + 1} \right)x + 1\) có đồ thị \(\left( C \right)\). Biết rằng khi \(m = {m_0}\) thì tiếp tuyến với đồ thị \(\left( C \right)\) tại điểm có hoành độ bằng \({x_0} = - 1\) đi qua \(A\left( {1;\,3} \right)\). Khẳng định nào sâu đây đúng?

Cho hàm số \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{a{x^2} + bx + 1}&{khi}&{x \ge 0}\\{ax - b - 1}&{khi}&{x < 0}\end{array}} \right.\). Khi hàm số \(y = f\left( x \right)\) có đạo hàm tại \({x_0} = 0\), hãy tính \(T = a + 2b\).

Cho hàm số \(y = {\sin ^2}x\). Tính \({y^{\left( {2018} \right)}}\left( \pi \right)\).

Cho hàm số $y = \dfrac{{x + 2}}{{x - 1}}$ có đồ thị $\left( C \right)$ và điểm $A\left( {0;\,a} \right)$. Hỏi có tất cả bao nhiêu giá trị nguyên của $a$ trong đoạn $\left[ { - 2018;\,2018} \right]$ để từ điểm $A$ kẻ được hai tiếp tuyến đến $\left( C \right)$ sao cho hai tiếp điểm nằm về hai phía của trục hoành?

Gọi $S$ là tập hợp các điểm thuộc đường thẳng$y = 2$ mà qua mỗi điểm thuộc $S$ đều kẻ được hai tiếp tuyến phân biệt tới đồ thị hàm số $y = \dfrac{{{x^2}}}{{x - 1}}$ đồng thời hai tiếp tuyến đó vuông góc với nhau. Tính tổng hoành độ $T$ của tất cả các điểm thuộc $S$.

Phương trình tiếp tuyến với đồ thị \(\left( C \right):\,y = 2{x^3} - 6{x^2} + 3\) có hệ số góc nhỏ nhất là

Gọi \(M\left( {{x_M};{y_M}} \right)\) là một điểm thuộc \(\left( C \right):y = {x^3} - 3{x^2} + 2\), biết tiếp tuyến của \(\left( C \right)\) tại \(M\) cắt \(\left( C \right)\) tại điểm \(N\left( {{x_N};{y_N}} \right)\) (khác \(M\)) sao cho \(P = 5x_M^2 + x_N^2\) đạt giá trị nhỏ nhất. Tính \(OM\).

Cho hàm số $y = \sqrt {{x^2} - 2x + 3} $ có đồ thị $\left( C \right)$ và điểm $A\left( {1;a} \right)$. Có bao nhiêu giá trị nguyên của $a$ để có đúng hai tiếp tuyến của $\left( C \right)$ đi qua $A$?

Cho hàm số \(y = {x^3} - 3x\) có đồ thị \(\left( C \right)\). Gọi \(S\) là tập hợp tất cả giá trị thực của \(k\) để đường thẳng \(d:y = k\left( {x + 1} \right) + 2\) cắt đồ thị \(\left( C \right)\) tại ba điểm phân biệt \(M,\)\(N,\)\(P\) sao cho các tiếp tuyến của \(\left( C \right)\) tại \(N\) và \(P\) vuông góc với nhau. Biết \(M\left( { - 1;2} \right)\), tính tích tất cả các phần tử của tập \(S\).

Cho đồ thị $\left( C \right):y = {x^3} - 3{x^2} - 9x + 10$ và điểm $A\left( {m;\, - 10} \right)$. Gọi $S$ là tập tất cả các giá trị thực của $m$ để có đúng $2$ tiếp tuyến của $\left( C \right)$ qua $A$. Tổng giá trị tất cả các phần tử của $S$ bằng

Cho hàm số \(y = {x^3} - m{x^2} - mx + 2m - 3\) có đồ thị là \(\left( C \right)\), với \(m\) là tham số thực. Gọi \(T\) là tập tất cả các giá trị nguyên của \(m\) để mọi đường thẳng tiếp xúc với \(\left( C \right)\) đều có hệ số góc dương. Tính tổng các phần tử của \(T\).

Cho hàm số \(y = {x^3} - 3x + 2\) có đồ thị \(\left( C \right)\). Hỏi có bao nhiêu điểm trên đường thẳng $d:y = 9x - 14$ sao cho từ đó kẻ được hai tiếp tuyến với \(\left( C \right)\).

Cho hàm số $y = {\left| x \right|^3} - 3{x^2} + 1$ có đồ thị $\left( C \right)$. Hỏi trên trục $Oy$ có bao nhiêu điểm $A$ mà qua $A$ có thể kẻ đến $\left( C \right)$ đúng ba tiếp tuyến?

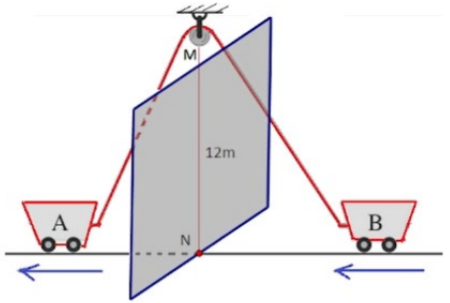
Trong hình vẽ, xe \(A\) kéo xe \(B\) bằng một sợi dây dài \(39\,m\) qua một ròng rọc ở độ cao \(12m\). Xe \(A\) xuất phát từ \(N\) và chạy với vận tốc không đổi \(2m/s\) theo chiều mũi tên.