Cho Hcn Abcd ( AD < AB ). Kẻ AH Vuông Góc BD. AH Cắt CD Tại I.a ...

HOC24

Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng

• Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn

Đóng Đăng nhập Đăng ký

Lớp học

• Lớp 12
• Lớp 11
• Lớp 10
• Lớp 9
• Lớp 8
• Lớp 7
• Lớp 6
• Lớp 5
• Lớp 4
• Lớp 3
• Lớp 2
• Lớp 1

Môn học

• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Đạo đức
• Tự nhiên và xã hội
• Khoa học
• Lịch sử và Địa lý
• Tiếng việt
• Khoa học tự nhiên
• Hoạt động trải nghiệm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Chủ đề / Chương

Bài học

HOC24

Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng

• Tất cả
• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Hãy tham gia nhóm Học sinh Hoc24OLM Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài

Câu hỏi

Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay Võ Thị Thảo Mai 13 tháng 8 2017 lúc 12:58

Cho hcn abcd ( AD < AB ). Kẻ AH vuông góc BD. AH cắt CD tại I.

a) CM AH. AI = BD.HD

b) AH cắt BC tại K. CM AH. AK = HB.DB

C) CM HA^2 = HI.HK

Lớp 9 Toán Những câu hỏi liên quan

• Trâm Nguyễn

17 tháng 9 2021 lúc 8:06

Bài 5. Cho hình chữ nhật ABCD, qua A kẻ đường vuông góc với BD tại H. Biết AB = 20 cm , AH = 12 cm a) Tính AD, HD, HB .b) AH cắt CD tại M. Chứng minh: DH.DB=AH.AM C) AH cắt BC tại K. Chứng minh; HA^ 2 =HM.HK

Xem chi tiết Lớp 9 Toán 1 1 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 18 tháng 9 2021 lúc 0:37

b: Xét ΔADM vuông tại D có DH là đường cao ứng với cạnh huyền AM

nên \(AH\cdot AM=AD^2\left(1\right)\)

Xét ΔADB vuông tại A có AH là đường cao ứng với cạnh huyền DB

nên \(DH\cdot DB=AD^2\left(2\right)\)

Từ (1) và (2) suy ra \(DH\cdot DB=AH\cdot AM\)

Đúng 0 Bình luận (0) Gửi Hủy

• Ngô Ngọc Linh

16 tháng 2 2021 lúc 19:47

Cho hình chữ nhật ABCD (AB>AD). Kẻ AH vuông góc với BD tại H, AH cắt CD tại K.

a. CM: tamgiac AHD đồng dạng tamgiac BAD. Tính AB biết AD=5cm, AH=4cm

b. CM: HA^2=HB.HD

c. Gọi I là trung điểm của CD. Tia BK cắt tia AD tại M, tia MI cắt AC tại N, tia BN cắt CD tại E. CM: DK=CE

Xem chi tiết Lớp 8 Toán Ôn tập: Tam giác đồng dạng 1 1 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 16 tháng 2 2021 lúc 21:24

a) Xét ΔAHD vuông tại H và ΔBAD vuông tại A có 

\(\widehat{ABD}\) chung

Do đó: ΔAHD∼ΔBAD(g-g)

Áp dụng định lí Pytago vào ΔADH vuông tại H, ta được:

\(AH^2+HD^2=AD^2\)

\(\Leftrightarrow HD^2=AD^2-AH^2=5^2-4^2=9\)

hay HD=3(cm)

Ta có: ΔAHD∼ΔBAD(cmt)

nên \(\dfrac{AH}{BA}=\dfrac{HD}{AD}=\dfrac{AD}{BD}\)

\(\Leftrightarrow\dfrac{4}{AB}=\dfrac{3}{5}\)

hay \(AB=\dfrac{20}{5}cm\)

Vậy: \(AB=\dfrac{20}{5}cm\)

b) Xét ΔAHD vuông tại H và ΔBHA vuông tại H có 

\(\widehat{HAD}=\widehat{HBA}\left(=90^0-\widehat{ADH}\right)\)

Do đó: ΔAHD∼ΔBHA(g-g)

⇔\(\dfrac{AH}{BH}=\dfrac{HD}{HA}\)(Các cặp cạnh tương ứng tỉ lệ)

hay \(HA^2=HB\cdot HD\)(đpcm)

Đúng 3 Bình luận (0) Gửi Hủy

• Cu Giai

7 tháng 8 2018 lúc 9:42

Cho hình chữ nhật ABCD có AD = 12cm, AB = 16 cm. Kẻ đường cao AH cuuar tam giác ABD. Đường thắng AH cắt DC tại I và BC tại K. Chứng minh AH2 = HI.HK

Xem chi tiết Lớp 8 Toán Câu hỏi của OLM 2 0 Gửi Hủy Hương Phạm 7 tháng 8 2018 lúc 10:34

\(\widehat{HAD}+\widehat{ADH}=90^0\)

\(\widehat{HAD}+\widehat{BAH}=90^0\)

=> \(\widehat{ADH}=\widehat{BAH}\)

C/m được: tam giác ADH đồng dạng với tam giác BAH theo t/h g.g

=> AH/HD=BH/AH

=>\(AH^2=HD.BH\)(1)

CMTT: tam giác HID đồng dạng vói tam giác HBK theo t/h g.g

=>HD/HI=HK/HB

=>HD.BH=HI/HK (2)

Từ (1) và (2) suy ra (đpcm)

Đúng 0 Bình luận (0) Gửi Hủy công 4 tháng 11 2018 lúc 20:58

chưa chặt chẽ

Đúng 0 Bình luận (0) Gửi Hủy

• An Đinh Khánh

19 tháng 8 2023 lúc 14:50 Cho hcn ABCD, Kẻ BH vuông góc với AC, Bh cắt CD tại E. Gọi tia BE cắt tia AD tại K,a) Cho AB= 4cm, BC= 3cm. Tính AC,AH,BHb) CM: BH.BE=CH.ACc)C/M góc ADH = góc ACKHelpppp Xem chi tiết Lớp 9 Toán 2 0 Gửi Hủy meme 19 tháng 8 2023 lúc 15:49

Để giải bài toán này, chúng ta có thể sử dụng định lí Euclid và các quy tắc về góc và đường thẳng. Hãy xem xét từng câu hỏi một.

a) Để tính AC, ta có thể sử dụng định lí Pythagoras trong tam giác ABC. Với AB = 4cm và BC = 3cm, ta có AC = √(AB^2 + BC^2). Tương tự, để tính AH và BH, ta có AH = AB và BH = BC.

b) Để chứng minh rằng BH.BE = CH.AC, ta có thể sử dụng các quy tắc về tỉ lệ đồng dạng của tam giác. Bằng cách chứng minh rằng tam giác AHB và tam giác CHB đồng dạng, ta có thể suy ra công thức trên.

c) Để chứng minh góc ADH = góc ACK, ta có thể sử dụng các quy tắc về góc đồng quy và góc nội tiếp. Bằng cách chứng minh rằng góc ADH và góc ACK đồng quy với góc nội tiếp tại cùng một cung, ta có thể suy ra bằng chứng cần thiết

Đúng 0 Bình luận (3) Gửi Hủy Nguyễn Lê Phước Thịnh CTV 19 tháng 8 2023 lúc 20:32

a: \(AC=\sqrt{AB^2+BC^2}=5\left(cm\right)\)

Xét ΔBAC vuông tại B có BH là đường cao

nên BH*AC=BA*BC

=>BH*5=3*4=12

=>BH=2,4cm

Xét ΔBAC vuông tại B có BH là đường cao

nên AH*AC=AB^2

=>AH=4^2/5=3,2cm

b: ΔBCE vuông tại C có CH là đường cao

nên BH*BE=BC^2

ΔBCA vuông tại B có BH là đường cao

nên CH*CA=BC^2

=>BH*BE=CH*CA

c: góc KDC=góc KHC=90 độ

=>KDHC nội tiếp

=>góc HCK+góc HDK=180 độ

mà góc HDK+góc ADH=180 độ

nên góc ADH=góc ACK

Đúng 0 Bình luận (0) Gửi Hủy

• Mèo Dương
• 

31 tháng 10 2023 lúc 21:54 Cho hình chữ nhật ABCD, AB9cm,AC12cm,kẻ AH vuông góc với BD tại Ha) Tính BD,AH và góc BDAb) Kẻ HI vuông góc AB.CM AI.ABDH.HBc) Đường thẳng AH cắt BC tại M, cắt DC tại N. CM HA2HM.HNgiúp tui giải ik mà làm ơnĐọc tiếp

Cho hình chữ nhật ABCD, AB=9cm,AC=12cm,kẻ AH vuông góc với BD tại H

a) Tính BD,AH và góc BDA

b) Kẻ HI vuông góc AB.CM AI.AB=DH.HB

c) Đường thẳng AH cắt BC tại M, cắt DC tại N. CM HA2=HM.HN

giúp tui giải ik mà làm ơn

Xem chi tiết Lớp 9 Toán 1 0 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 31 tháng 10 2023 lúc 22:58

a: ΔABD vuông tại A

=>\(BD^2=AB^2+AD^2\)

=>\(BD^2=9^2+12^2=225\)

=>BD=15(cm)

Xét ΔABD vuông tại A có AH là đường cao

nên \(AH\cdot BD=AB\cdot AD\)

=>\(AH\cdot15=12\cdot9=108\)

=>AH=108/15=7,2(cm)

XétΔABD vuông tại A có \(sinBDA=\dfrac{AB}{BD}=\dfrac{9}{15}=\dfrac{3}{5}\)

nên \(\widehat{BDA}\simeq37^0\)

b: Xét ΔAHB vuông tại H có HI là đường cao

nên \(AI\cdot AB=AH^2\left(1\right)\)

Xét ΔABD vuông tại A có AH là đường cao

nên \(AH^2=HD\cdot HB\left(2\right)\)

Từ (1) và (2) suy ra \(AI\cdot AB=HD\cdot HB\)

c: Xét ΔHDN vuông tại H và ΔHMB vuông tại H có

\(\widehat{HDN}=\widehat{HMB}\left(=90^0-\widehat{DBC}\right)\)

Do đó: ΔHDN đồng dạng với ΔHMB

=>HD/HM=HN/HB

=>\(HM\cdot HN=HD\cdot HB=HA^2\)

Đúng 2 Bình luận (1) Gửi Hủy

• Mèo Dương
• 

31 tháng 10 2023 lúc 21:35 Cho hình chữ nhật ABCD, AB9cm,AC12cm,kẻ AH vuông góc với BD tại Ha) Tính BD,AH và góc BDAb) Kẻ HI vuông góc AB.CM AI.ABDH.HBc) Đường thẳng AH cắt BC tại M, cắt DC tại N. CM HA2HM.HNgiúp tui vs tui đag cần lời giải gấp Đọc tiếp

Cho hình chữ nhật ABCD, AB=9cm,AC=12cm,kẻ AH vuông góc với BD tại H

a) Tính BD,AH và góc BDA

b) Kẻ HI vuông góc AB.CM AI.AB=DH.HB

c) Đường thẳng AH cắt BC tại M, cắt DC tại N. CM HA2=HM.HN

giúp tui vs tui đag cần lời giải gấp 

Xem chi tiết Lớp 9 Toán 1 0 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 31 tháng 10 2023 lúc 22:59

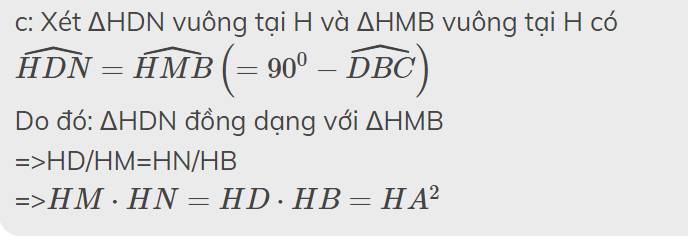
Đúng 1 Bình luận (1) Gửi Hủy

• Minh_MinhK

20 tháng 3 2021 lúc 19:40

Cho Tam giác ABC vuông tại A biết AB = 6 cm ,AC =8cm .kẻ phân giác BD a) Tính BC,AD,CD b) Kẻ đg cao AH, BD tại E. CM tam giác AED cân tại A c) CM CA/AH=AD/EH đ) Từ C kẻ đt vuông góc vs BD cắt AB tại F CM BF/BD=BC/BD Giúp mình vs ạk

Xem chi tiết Lớp 8 Toán 1 1 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 20 tháng 3 2021 lúc 20:02

a) Áp dụng định lí Pytago vào ΔABC vuông tại A,ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=6^2+8^2=100\)

hay BC=10(cm)

Vậy: BC=10cm

Đúng 0 Bình luận (1) Gửi Hủy

• Đông Phương

27 tháng 10 2021 lúc 10:23

Cho hình chữ nhật ABCD có AB = 24cm, AD = 26 cm. Kẻ AH vuông góc với BD tại H. a)Tính độ dài HD, AH. b)Tia AH cắt CD tại M. Chứng minh AH.AM = DH.DB

Xem chi tiết Lớp 9 Toán 1 1 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 27 tháng 10 2021 lúc 14:41

b: Xét ΔBAD vuông tại A có AH là đường cao

nên \(DH\cdot DB=AD^2\left(1\right)\)

Xét ΔADM vuông tại D có DH là đường cao

nên \(AH\cdot AM=AD^2\left(2\right)\)

Từ (1) và (2) suy ra \(DH\cdot DB=AH\cdot AM\)

Đúng 0 Bình luận (0) Gửi Hủy

• Lê Hoàng Yến Nhi

7 tháng 5 2019 lúc 20:54

Cho hình chữ nhật ABCD (AB>AD). Kẻ AH vuông góc với BD tại H, AH cắt CD tại K.

a. CM: tamgiac AHD đồng dạng tamgiac BAD. Tính AB biết AD=5cm, AH=4cm

b. CM: HA^2=HB.HD

c. Gọi I là trung điểm của CD. Tia BK cắt tia AD tại M, tia MI cắt AC tại N, tia BN cắt CD tại E. CM: DK=CE

Xem chi tiết Lớp 8 Toán Ôn tập cuối năm phần hình học 1 0 Gửi Hủy Hoaa 7 tháng 5 2019 lúc 21:04

a)Vì tam giác ABCD là HCN =>góc A = 90 độ

xét tam giác AHD VÀ TAM GIÁC ABD CÓ ;

GÓC D CHUNG

GÓC AHD = GÓC A

=>TAM GIÁC AHD ĐỒNG DẠNG VỚI TAM GIÁC BAD(G.G)

B)vÌ TAM GIÁC AHD ĐỒNG DẠNG VỚI TAM GIÁC BAD (THEO CÂU A)

=>GÓC HAD=GÓC ABD(1)

XÉT TAM GIÁC AHD VÀ TAM GIÁC AHB CÓ :

GÓC AHD = GÓC AHB (=90 ĐỘ )

GÓC HAD= GÓC ABD (THEO 1)

=>TAM GIÁC AHD ĐỒNG DẠNG VỚI TAM GIÁC BHA(G.G)

=>AH/HD=BH/AH

=>AH^2=BH.HD(DPCM)

Đúng 5 Bình luận (0) Gửi Hủy

Khoá học trên OLM (olm.vn)

• Toán lớp 9
• Ngữ văn lớp 9
• Tiếng Anh lớp 9
• Vật lý lớp 9
• Hoá học lớp 9
• Sinh học lớp 9
• Lịch sử lớp 9
• Địa lý lớp 9