Cho Hình 57 Chứng Minh NS Vuông Góc LM

Trang chủ » Cho Hình 57 Chứng Minh Ns Vuông Góc Lm » Cho Hình 57 Chứng Minh NS Vuông Góc LM

Có thể bạn quan tâm

Giải Toán 7 Luyện tập trang 83

Video giải Bài 59 trang 83 Toán lớp 7 Tập 2

Bài 59 trang 83 Toán lớp 7 Tập 2: Cho hình 57.

a) Chứng minh NS ⊥ LM

b) Khi góc LNP = 50o, hãy tính góc MSP và góc PSQ.

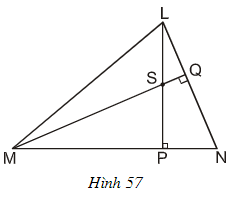
Tài liệu VietJack

Lời giải:

a) Trong ΔMNL có:

LP ⊥ MN nên LP là đường cao của ΔMNL.

MQ ⊥ NL nên MQ là đường cao của ΔMNL.

Mà LP, MQ cắt nhau tại điểm S nên suy ra S là trực tâm của ΔMNL.

Vì ba đường cao của tam giác cắt nhau tại một điểm nên suy ra NS là đường cao của tam giác MNL. Suy ra SN ⊥ ML.

b)

Xét ΔNMQ vuông tại Q ta có:

LNP^+QMN^=90°⇒QMN^=90°−LNP^=90°−50°=40°

Xét ΔMSP vuông tại P ta có:

MSP^+PMS^=90°⇒MSP^=90°−PMS^=90°−40°=50°

Vì và là hai góc kề bù nên ta có:

MSP^+PSQ^=180°⇒PSQ^=180°−MSP^=180°−50°=130°

Xem thêm lời giải bài tập Toán lớp 7 hay, chi tiết khác:

Bài 58 trang 83 Toán 7 Tập 2: Hãy giải thích tại sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm ở bên ngoài tam giác...

Bài 60 trang 83 Toán 7 Tập 2: Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K)...

Bài 61 trang 83 Toán 7 Tập 2: Cho tam giác ABC không vuông. Gọi H là trực tâm của nó...

Bài 62 trang 83 Toán 7 Tập 2: Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân...

Từ khóa » Cho Hình 57 Chứng Minh Ns Vuông Góc Lm