Cho Hình Bình Hành ABCD. Tổng Các Vectơ A B → A C →... - Hoc24

HOC24

Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng

• Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn

Đóng Đăng nhập Đăng ký

Lớp học

• Lớp 12
• Lớp 11
• Lớp 10
• Lớp 9
• Lớp 8
• Lớp 7
• Lớp 6
• Lớp 5
• Lớp 4
• Lớp 3
• Lớp 2
• Lớp 1

Môn học

• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Đạo đức
• Tự nhiên và xã hội
• Khoa học
• Lịch sử và Địa lý
• Tiếng việt
• Khoa học tự nhiên
• Hoạt động trải nghiệm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Chủ đề / Chương

Bài học

HOC24

Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng

• Tất cả
• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Hãy tham gia nhóm Học sinh Hoc24OLM Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài

Câu hỏi

Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay Pham Trong Bach 24 tháng 3 2017 lúc 3:30 Cho hình bình hành ABCD. Tổng các vectơ A B → + A C → + A D →  làĐọc tiếp

Cho hình bình hành ABCD. Tổng các vectơ A B → + A C → + A D →  là

Lớp 10 Toán Những câu hỏi liên quan

• Truc Thanh

12 tháng 9 2021 lúc 21:00

Cho hình bình hành ABCD có tâm là O . Tìm các vectơ từ 5 điểm A B C D O  a). Bằng vectơ AB ; OB. b). Có độ dài bằng OB .

Xem chi tiết Lớp 10 Toán Chương 1: VECTƠ 2 0 Gửi Hủy Nguyễn Việt Lâm CTV 12 tháng 9 2021 lúc 21:23

Bằng \(\overrightarrow{AB}\) là \(\overrightarrow{DC}\)

Bằng \(\overrightarrow{OB}\) là \(\overrightarrow{DO}\)

Có độ dài bằng OB là \(\overrightarrow{OB};\overrightarrow{BO};\overrightarrow{OD};\overrightarrow{DO}\)

Đúng 1 Bình luận (0) Gửi Hủy Ikino Yushinomi 12 tháng 9 2021 lúc 21:26

a) Bằng vectơ AB :\(\overrightarrow{DC}\)Bằng vectơ OB :\(\overrightarrow{DO}\)b)Có độ dài bằng OB :\(\overrightarrow{OD}, \overrightarrow{DO}, \overrightarrow{BO}\) 

Đúng 0 Bình luận (0) Gửi Hủy

• Pham Trong Bach

2 tháng 6 2018 lúc 5:25 Cho hình bình hành ABCD. A B →   +   A C →   + A D → Tổng các vectơ là A.  A C → B. 2 C . 3 D. 5Đọc tiếp

Cho hình bình hành ABCD. A B →   +   A C →   + A D → Tổng các vectơ là

A.  A C →

B. 2

C . 3

D. 5

Xem chi tiết Lớp 11 Toán 1 0 Gửi Hủy Cao Minh Tâm 2 tháng 6 2018 lúc 5:26

Đúng 0 Bình luận (0) Gửi Hủy

• Manh Duy

27 tháng 9 2021 lúc 18:01

Cho hình bình hành ABCD có O = AC n BD a,Tìm các vectơ khác vectơ O + Cùng phương với vectơ OA + Cùng chiều với vectơ BD b, Tìm các vectơ + bằng với AB + bằng với CO

Xem chi tiết Lớp 10 Toán §1. Các định nghĩa 0 0 Gửi Hủy

• Tiểu Z

7 tháng 8 2021 lúc 17:50 Câu 8: Cho hình bình hành ABCD tâm O. Các vectơ khác 0 ngược hướng với OB làA. BD OD , . B. BD OD BO , , . C. DB DO , . D. BD BO , .Câu 9: Cho ba điểm A, B, C thẳng hàng, trong đó điểm B nằm giữa hai điểm A và C. Khi đó các cặp vectơ nào sau đây cùng hướng?A. CB và AB. B. AB và AC. C. AB và CB . D. BA và BC.Câu 10: Cho một đa giác 1 2 2019 A A A ... có 2019 cạnh. Số vectơ khác 0 có điểm đầu và điểm cuối được tạo thành từ các đỉnh của đa giácA. 4074342. B. 8148684. C. 4076361. D. 8152722Đọc tiếp

Câu 8: Cho hình bình hành ABCD tâm O. Các vectơ khác 0 ngược hướng với OB là

A. BD OD , . B. BD OD BO , , . C. DB DO , . D. BD BO , .

Câu 9: Cho ba điểm A, B, C thẳng hàng, trong đó điểm B nằm giữa hai điểm A và C. Khi đó các cặp vectơ nào sau đây cùng hướng?

A. CB và AB. B. AB và AC. C. AB và CB . D. BA và BC.

Câu 10: Cho một đa giác 1 2 2019 A A A ... có 2019 cạnh. Số vectơ khác 0 có điểm đầu và điểm cuối được tạo thành từ các đỉnh của đa giác

A. 4074342. B. 8148684. C. 4076361. D. 8152722

Xem chi tiết Lớp 10 Toán 0 0 Gửi Hủy

• Bài 4
• 

SGK Chân trời sáng tạo trang 102 25 tháng 9 2023 lúc 21:45 Cho hình bình hành ABCD hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho overrightarrow {CE}  overrightarrow {AN} (hình 1)a) Tìm tổng của các vectơ:overrightarrow {NC} và overrightarrow {MC} ; overrightarrow {AM} và overrightarrow {CD} ; overrightarrow {AD} và overrightarrow {NC} b) Tìm các vectơ hiệu:overrightarrow {NC}  - overrightarrow {MC} ; overrightarrow {AC}  - overrightarrow {BC} ; overrightarrow {AB}  - overrightarrow {ME} . c) Chứng minh overrightarrow {AM} ...Đọc tiếp

Cho hình bình hành ABCD hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho \(\overrightarrow {CE}  = \overrightarrow {AN} \) (hình 1)

a) Tìm tổng của các vectơ:

\(\overrightarrow {NC} \) và \(\overrightarrow {MC} \); \(\overrightarrow {AM} \) và \(\overrightarrow {CD} \); \(\overrightarrow {AD} \) và \(\overrightarrow {NC} \)

b) Tìm các vectơ hiệu:

\(\)\(\overrightarrow {NC}  - \overrightarrow {MC} \); \(\overrightarrow {AC}  - \overrightarrow {BC} \); \(\overrightarrow {AB}  - \overrightarrow {ME} \).

 c) Chứng minh \(\overrightarrow {AM}  + \overrightarrow {AN}  = \overrightarrow {AB}  + \overrightarrow {AD} \)

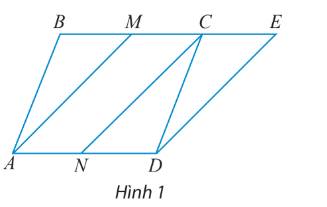
Xem chi tiết Lớp 10 Toán Bài tập cuối chương V 1 0 Gửi Hủy Hà Quang Minh Giáo viên CTVVIP 25 tháng 9 2023 lúc 21:46

a) Ta có: \(\overrightarrow {CE}  = \overrightarrow {AN}  \Rightarrow CE//AN\) và \(CE = AN = ND = BM = MC\)

Suy ra \(\overrightarrow {MC}  = \overrightarrow {CE} \)

+) \(\overrightarrow {NC}  + \overrightarrow {MC}  = \overrightarrow {NC}  + \overrightarrow {CE}  = \overrightarrow {NE} \)

+) ABCD là hình bình hành nên \(\overrightarrow {CD}  = \overrightarrow {BA} \)

\(\overrightarrow {AM}  + \overrightarrow {CD}  = \overrightarrow {AM}  + \overrightarrow {BA}  = \overrightarrow {BM} \)

+) Ta có \(\overrightarrow {MC}  = \overrightarrow {AN}  \Rightarrow AMCN\) là hình bình hành nên \(\overrightarrow {NC}  = \overrightarrow {AM} \)

\(\overrightarrow {AD}  + \overrightarrow {NC}  = \overrightarrow {AD}  + \overrightarrow {AM}  = \overrightarrow {AE} \) (vì AMED là hình bình hành)

b) Ta có:

+) \(\overrightarrow {NC}  - \overrightarrow {MC}  = \overrightarrow {NC}  + \overrightarrow {CM}  = \overrightarrow {NM} \)

+) \(\overrightarrow {AC}  - \overrightarrow {BC}  = \overrightarrow {AC}  + \overrightarrow {CB}  = \overrightarrow {AB} \)

+) \(\overrightarrow {AB}  - \overrightarrow {ME}  = \overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {AB}  + \overrightarrow {DA}  = \overrightarrow {DB} \)

c) Ta có:

\(\overrightarrow {AM}  + \overrightarrow {AN}  = \overrightarrow {AM}  + \overrightarrow {MC}  = \overrightarrow {AC} \)

Áp dụng quy tắc hình bình hành vào hình bình hành ABCD ta có

\(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} \)

Từ đó suy ra \(\overrightarrow {AM}  + \overrightarrow {AN}  = \overrightarrow {AB}  + \overrightarrow {AD} \) (đpcm)

Đúng 0 Bình luận (0) Gửi Hủy

• Tuấn Phạm

15 tháng 11 2023 lúc 20:28

1)Cho hình bình hành ABCD, xác định các vectơ DA+DC,AB+DA. 2)Cho 5 điểm A, B, C, D, E. Chứng minh rằng: AC-ED+CD+EC-BC = AB 3)Cho hình vuông ABCD, tâm O cạnh bằng a. a) Xác định vecto BA+DA+AC, AB+CA+BC, AB+AC. b) Tính độ dài vecto DA+DC, AB-BC

Xem chi tiết Lớp 10 Toán Câu hỏi của OLM 1 0 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 27 tháng 9 2025 lúc 20:39

1: ABCD là hình bình hành

=>\(\overrightarrow{DA}+\overrightarrow{DC}=\overrightarrow{DB}\)

\(\overrightarrow{AB}+\overrightarrow{DA}=\overrightarrow{DA}+\overrightarrow{AB}=\overrightarrow{DB}\)

2: \(\overrightarrow{AC}-\overrightarrow{ED}+\overrightarrow{CD}+\overrightarrow{EC}-\overrightarrow{BC}\)

\(=\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EC}+\overrightarrow{CB}\)

\(=\overrightarrow{AD}+\overrightarrow{DE}+\overrightarrow{EC}+\overrightarrow{CB}\)

\(=\overrightarrow{AE}+\overrightarrow{EC}+\overrightarrow{CB}=\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AB}\)

3:

a: \(\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}\)

\(=-\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{0}\)

\(\overrightarrow{AB}+\overrightarrow{CA}+\overrightarrow{BC}\)

\(=\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BC}\)

\(=\overrightarrow{CB}+\overrightarrow{BC}=\overrightarrow{0}\)

Gọi H là trung điểm của BC

Xét ΔABC có AH là đường trung tuyến

nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\cdot\overrightarrow{AH}\)

b: ABCD là hình vuông

=>\(DB^2=DA^2+AB^2\)

=>\(DB^2=a^2+a^2=2a^2\)

=>\(DB=a\sqrt2\)

ABCD là hình vuông

=>\(\overrightarrow{DA}+\overrightarrow{DC}=\overrightarrow{DB}\)

=>\(\left|\overrightarrow{DA}+\overrightarrow{DC}\right|=DB=a\sqrt2\)

\(\overrightarrow{AB}-\overrightarrow{CB}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\)

=>\(\left|\overrightarrow{AB}-\overrightarrow{CB}\right|=CA=a\sqrt2\)

Đúng 0 Bình luận (0) Gửi Hủy

• Nguyễn Duy

11 tháng 8 2016 lúc 12:41

Cho hình thang ABCD ( AB // CD ) và điểm M nằm trong hình thang ABCD. Kẻ các hình bình hành MAED, MBFC. Chứng minh hai vectơ EF và vectơ AB cùng phương.

Xem chi tiết Lớp 10 Toán §2. Tổng và hiệu của hai vectơ 0 0 Gửi Hủy

• Bài 1.50

SBT trang 45 8 tháng 4 2017 lúc 12:52

Cho hai hình bình hành ABCD và EBEF với A, D, F không thẳng hàng. Dựng các vectơ \(\overrightarrow{EH}\) và \(\overrightarrow{FG}\) bằng vectơ \(\overrightarrow{AD}\). Chứng minh tứ giác CDGH là hình bình hành ?

Xem chi tiết Lớp 10 Toán Ôn tập chương I 1 0 Gửi Hủy Nguyen Thuy Hoa 19 tháng 5 2017 lúc 14:36

\(\overrightarrow{EH}=\overrightarrow{AD},\overrightarrow{FG}=\overrightarrow{AD}\Rightarrow\overrightarrow{EH}=\overrightarrow{FG}\)

=> Tứ giác FEHG là hình bình hành

=> \(\overrightarrow{GH}=\overrightarrow{FE}\) (1)

Ta có \(\overrightarrow{DC}=\overrightarrow{AB},\overrightarrow{AB}=\overrightarrow{FE}\)

=> \(\overrightarrow{DC}=\overrightarrow{FE}\) (2)

Từ (1) và (2) ta có \(\overrightarrow{GH}=\overrightarrow{DC}\)

Vậy tứ giác GHCD là hình bình hành.

Đúng 0 Bình luận (0) Gửi Hủy

• Pham Trong Bach

5 tháng 1 2017 lúc 11:35  Trong không gian cho hai hình bình hành ABCD và A’B’C’D’ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ  B B → ,   C C → ,   D D →  đồng phẳng.Đọc tiếp

 Trong không gian cho hai hình bình hành ABCD và A’B’C’D’ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ  B B ' → ,   C C ' → ,   D D ' →  đồng phẳng.

Xem chi tiết Lớp 11 Toán 1 0 Gửi Hủy Cao Minh Tâm 5 tháng 1 2017 lúc 11:35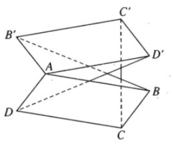

Ta có: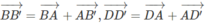 

Do đó: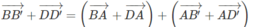 

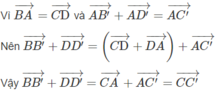
Hệ thức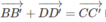 

 biểu thị sự đồng phẳng của ba vectơ  B B ' → ,   C C ' → ,   D D ' →

Đúng 0 Bình luận (0) Gửi Hủy

Khoá học trên OLM (olm.vn)

• Toán lớp 10 (Kết nối tri thức với cuộc sống)
• Toán lớp 10 (Cánh Diều)
• Toán lớp 10 (Chân trời sáng tạo)
• Ngữ văn lớp 10 (Kết nối tri thức với cuộc sống)
• Ngữ văn lớp 10 (Cánh Diều)
• Ngữ văn lớp 10 (Chân trời sáng tạo)
• Tiếng Anh lớp 10 (i-Learn Smart World)
• Tiếng Anh lớp 10 (Global Success)
• Vật lý lớp 10 (Kết nối tri thức với cuộc sống)
• Vật lý lớp 10 (Cánh diều)
• Hoá học lớp 10 (Kết nối tri thức với cuộc sống)
• Hoá học lớp 10 (Cánh diều)
• Sinh học lớp 10 (Kết nối tri thức với cuộc sống)
• Sinh học lớp 10 (Cánh diều)
• Lịch sử lớp 10 (Kết nối tri thức với cuộc sống)
• Lịch sử lớp 10 (Cánh diều)
• Địa lý lớp 10 (Kết nối tri thức với cuộc sống)
• Địa lý lớp 10 (Cánh diều)
• Giáo dục kinh tế và pháp luật lớp 10 (Kết nối tri thức với cuộc sống)
• Giáo dục kinh tế và pháp luật lớp 10 (Cánh diều)
• Lập trình Python cơ bản