Cho Lục Giác đều ABCDEF . A' ; B' ; C' ; D' ; E' ; F' , Là Trung điểm AB ...

Học liệu Hỏi đáp Đăng nhập Đăng ký

• Học bài
• Hỏi bài
• Kiểm tra
• ĐGNL
• Thi đấu
• Thư viện số
• Bài viết Cuộc thi Tin tức Blog học tập
• Trợ giúp
• Về OLM

OLM App phiên bản mới, cập nhật trải nghiệm ngay!

🔥ĐẤU TRƯỜNG TRỞ LẠI, THỬ THÁCH TĂNG CẤP!!! THAM GIA NGAY

Chính thức mở đề thi thử tốt nghiệp THPT trên máy tính từ 27/12/2025, xem ngay.

OLM Class tuyển sinh lớp bứt phá học kỳ II! Đăng ký ngay

• Mẫu giáo
• Lớp 1
• Lớp 2
• Lớp 3
• Lớp 4
• Lớp 5
• Lớp 6
• Lớp 7
• Lớp 8
• Lớp 9
• Lớp 10
• Lớp 11
• Lớp 12
• ĐH - CĐ

K Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xác nhận câu hỏi phù hợp

×

Chọn môn học Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên Mua vip

• Tất cả
• Mới nhất
• Câu hỏi hay
• Chưa trả lời
• Câu hỏi vip

SX super xity 18 tháng 12 2015 - olm

Cho lục giác đều ABCDEF . A' ; B' ; C' ; D' ; E' ; F' , là trung điểm AB , CD , DE , EF , FA

Chứng minh A'B'C'D'E'F' là lục giác đều

Giải chi tiết giùm nha

#Hỏi cộng đồng OLM #Toán lớp 8 1 NQ Nguyễn Quốc Khánh 18 tháng 12 2015

Theo đường tb tam giác

A'B'=1/2AC

B'C'=1/2BD

C'D'=1/2CE

D'E'=1/2DF

E'F'=1/2AE

A'F'=1/2BF

Mà AC=BD=CE=DF=AE=BF(tính chất lục giác)

=>A'B'C'D'E'F' là lục giác đều

Đúng(0) HK HASUN K. 25 tháng 11 2016 - olm

cho lục giác đều ABCDEF gọi A' B' C' D' E' F' lần lượt là trung điểm của các cạnh AB,BC,CD,DE,EF,FA chứng minh A'B'C'D'E'F' là lục giác đều

MẤY BN ĐANG ON GIẢI BÀI NÀY GIÚP MK VỚI MAI MK PHẢI NỘP RÙI

#Hỏi cộng đồng OLM #Toán lớp 8 0 DH Đào Hải Yến 15 tháng 10 2016

cho lục giác đều ABCDEF có góc A=góc B=góc C=góc D=góc E=góc F và AB<DE,EF<BC, CD<AF.CMR: DE-AB = BC - EF = AF- CD

 

#Hỏi cộng đồng OLM #Toán lớp 8 0 NL Ngô Linh 25 tháng 11 2017 - olm

Bài 3: Cho lục giác ABCDEF có số đo các góc (tính theo độ) là 1 số nguyên và góc A-góc B=góc B-góc C=góc C-góc D=góc D-góc E=góc E-góc F. Tính giá trị lớn nhất của góc A.Bài 4: Cho lục giác đều ABCDEF. M, N lần lượt là trung điểm của CD, DE. AM cắt BN tại I.a) Góc AIB=?b) Góc OID=? (biết O là tâm của lục giác đều)

#Hỏi cộng đồng OLM #Toán lớp 8 0 DB Đào Bảo 26 tháng 11 2021

Cho lục giác lồi abcdef có các cặp cạnh đối ab và de, bc và ef, CD và ef vừa song song vừa bằng nhau. Lục giác abcdef có nhất thiết là lục giác đều không

 

#Hỏi cộng đồng OLM #Toán lớp 8 0 DP Dat Phan 12 tháng 3 2020 - olm

cho lục giác đều abcdef các điểm m, n, p lần lượt là trung điểm các cạnh ab ,cd ,ef . cmr mnp là tam giác đều

#Hỏi cộng đồng OLM #Toán lớp 8 0 LL Lạnh Lùng Thì Sao 2 tháng 12 2015 - olm

CHo hình thoi ABCD có góc A=60độ. GỌi E, F, G, H lần lượt là trung điểm cyả cạnh AB,BC,CD,DA.Chứng minh rằng đa giác ÈGHD là lục giác đều 

Vẽ hình giúp mình nha

Giải chi tiết tí đừng rút gọn nha

#Hỏi cộng đồng OLM #Toán lớp 8 1 LN Lynh Ny Hann 2 tháng 12 2015

Số đo một góc trong lục giác đều là :\(180\times\left(6-2\right):6=720:6=120\left(độ\right)\)

ABCD là hình thoi =>AB=BC=CD=AD hay 1/2AB=1/2BC=1/2CD=1/2AD

Tam giác AHE có AH=AE (AH=1/2AD;AE=1/2AB)

=> Tam giác AHE cân . Mà A =60 (độ)

=> Tam giác AHE đều nên AHE=AEH=60 (độ)

Mặt khác góc DHE và góc HEB lần lượt kề bù vs AHE và AEH

=>DHE=HEB=120 (độ)

C/m tương tự ta có : HGF=BFG=120 (độ)

Lại có : ABCD là hình thoi có A =60 =>C=60 và D=B=120 (độ)

Lục giác HEBFGD có số đo mỗi góc bằng 120(độ) (cmt)

=> HEBFGD là lục giác đều

....................Đpcm

Hay cách khác cậu có thể c/m lục giác đều bằng cách c/m 6 cạnh bằng nhau thì sẽ dễ và nhanh hơn cách làm này,đương nhiên mk cux pit c/m cách lm đó n mk k tkick z pn tham khảo cách làm này na mặc dù nó hơi dài .!!!

Đúng(1) PT Pham Trong Bach 21 tháng 9 2018

Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

#Hỏi cộng đồng OLM #Toán lớp 10 1 CM Cao Minh Tâm 21 tháng 9 2018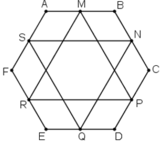

Gọi G là trọng tâm tam giác MPR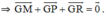 

Ta cần đi chứng minh G cũng là trọng tâm của ΔNQS bằng cách chứng minh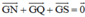 

Thật vậy ta có:

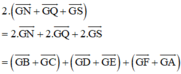
(Vì N, Q, S lần lượt là trung điểm của BC, DE, FA)

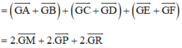
(Vì M, P, R là trung điểm AB, CD, EF)

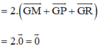
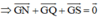 hay G cũng là trọng tâm của ΔNQS.

Vậy trọng tâm ΔMPR và ΔNQS trùng nhau.

Đúng(0) NT Nguyễn Thị Hồng Nhung 22 tháng 3 2016

Cho ABCDEF là lục giác lồi nội tiếp đường tròn bán kính R có các cạnh AB=CA=EF=R. Chứng minh rằng trung điểm 3 cạnh BC, DE, FA là đỉnh của một tam giác đều.

#Hỏi cộng đồng OLM #Toán lớp 11 1 NH Nguyễn Hòa Bình 22 tháng 3 2016

Ta cần chứng minh tam giác MNP là tam giác cân và có một góc bằng \(\frac{\Pi}{3}\)

Giả sử  lục giacs có hướng âm, kí hiệu \(f\) là phép quay vec tơ theo góc \(-\frac{\Pi}{3}\) và M, N. P theo thứ tự là trung điểm FA, BC, DE

Khi đó AB=BO, CD=DO=OC, EF=FO=OE nên các tam giác ABO, CDO, EFO đều và có hướng âm

Suy ra \(f\left(\overrightarrow{AB}\right)=\overrightarrow{AO}\), \(f\left(\overrightarrow{OC}\right)=\overrightarrow{OD}\), \(f\left(\overrightarrow{FO}\right)=\overrightarrow{FE}\)

Từ đó ta có :

\(f\left(\overrightarrow{MN}\right)=f\left(\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{FC}\right)\right)=\frac{1}{2}\left(f\left(\overrightarrow{AB}\right)+f\left(\overrightarrow{FC}\right)\right)\)

                \(=\frac{1}{2}\left(\overrightarrow{AO}\right)+\overrightarrow{OD}+\overrightarrow{FE}=\frac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{FE}\right)\)

                \(=\overrightarrow{MP}\)

Suy ra tam giác MNP cân và có góc PMN = \(\frac{\Pi}{3}\) => Điều phải chứng minh

Đúng(0) SG Sách Giáo Khoa 8 tháng 4 2017

Cho lục giác ABCDEF. Gọi M, N, P, Q, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm ?

#Hỏi cộng đồng OLM #Toán lớp 10 2 HH Hoang Hung Quan 19 tháng 5 2017

Giải:

Gọi \(G\) là trọng tâm của \(\Delta MPR\) và \(K\) là trọng tâm của của \(\Delta NQS\)

\(\Rightarrow\) Ta cần chứng minh: \(K\) và \(G\) trùng nhau

Vì \(G\) là trọng tâm của \(\Delta MPR\) nên ta có:

\(3\overrightarrow{KG}=\overrightarrow{KM}+\overrightarrow{KP}+\overrightarrow{KR}\)

\(=\dfrac{1}{2}\left(\overrightarrow{KA}+\overrightarrow{KB}+\overrightarrow{KC}+\overrightarrow{KD}+\overrightarrow{KE}+\overrightarrow{KF}\right)\) (t/c trung điểm)

\(=\dfrac{1}{2}\left(\overrightarrow{KB}+\overrightarrow{KC}\right)+\dfrac{1}{2}\left(\overrightarrow{KD}+\overrightarrow{KE}\right)+\dfrac{1}{2}\left(\overrightarrow{KA}+\overrightarrow{KF}\right)\)

\(=\overrightarrow{KN}+\overrightarrow{KQ}+\overrightarrow{KS}=\overrightarrow{0}\) (Vì \(K\) là trọng tâm của của \(\Delta NQS\))

\(\Rightarrow\) Đpcm

Đúng(0) AT Anh Triêt 20 tháng 5 2017

Đúng(0) Xem thêm câu trả lời Xếp hạng Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên

• Tuần
• Tháng
• Năm

• B 🐊Bombardiro💣Crocodilo✈️ 7 GP
• TK Tonko kakun 6 GP
• DM ༒☬Đăng Minh☬༒ (Meokonhonguongthuoc) 6 GP
• E ✦ ꧁𝓑é✿𝓬𝓱í𝓹꧂ ✦ 6 GP
• NB Nguyễn Bá Tĩnh 4 GP
• NT Nguyễn Thanh Trúc 4 GP
• NT Nguyễn Trường An 4 GP
• NT Nguyễn Thị Bảo Linh 4 GP
• NT Nguyễn Trường Tiến 4 GP
• O ꧁༺©ⓤ✞ঔৣ㊎۝ɦƯղɕლɑꜱζℰℜɦỒղղɦ¡Êղ2ƙ13✿❤☯... VIP 4 GP

Học liệu Hỏi đáp Link rút gọn Link rút gọn Để sau Đăng ký

Các khóa học có thể bạn quan tâm

× Mua khóa học Tổng thanh toán: 0đ (Tiết kiệm: 0đ) Tới giỏ hàng Đóng ×

Yêu cầu VIP

×

Học liệu này đang bị hạn chế, chỉ dành cho tài khoản VIP cá nhân, vui lòng nhấn vào đây để nâng cấp tài khoản.