Chứng Minh 3 điểm Thẳng Hàng - Chuyên đề Toán Lớp 9 Luyện Thi ...

Cách chứng minh 3 điểm thẳng hàng

• A. Cách chứng minh ba điểm thẳng hàng
• B. Bài tập chứng minh ba điểm thẳng hàng
• C. Bài tập tự luyện chứng minh ba điểm thẳng hàng

Bài tập Toán 9: Chứng minh ba điểm thẳng hàng là một dạng toán hình xuất hiện nhiều trong đề thi tuyển sinh vào lớp 10 môn Toán. Tài liệu được GiaiToan.com biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.

A. Cách chứng minh ba điểm thẳng hàng

Cách 1: Sử dụng hai góc kề bù có ba điểm nằm trên hai cạnh là hai tia đối nhau.

Cách 2: Hai đường thẳng cùng đi qua hai trong ba điểm ấy cùng vuông góc với đường thẳng thứ ba

Cách 3: Hai đường thẳng cùng đi qua hai trong ba điểm ấy cùng song song với đường thẳng thứ ba

Cách 4: Sử dụng tính chất đường phân giác của một góc, tính chất đường trung trực của đoạn thẳng, tính chất ba đường cao của tam giác.

B. Bài tập chứng minh ba điểm thẳng hàng

Ví dụ 1: Cho nửa đường đường tròn (O; R), đường kính AB. Một điểm M cố định thuộc đoạn thẳng OB (M khác B và M khác O). Đường thẳng d vuông góc với AB tại M cắt nửa đường tròn đã cho tại N. Trên cung NB lấy điểm E bất kì (E khác B và E khác N). Tia BE cắt đường thẳng d tại C, đường thẳng AC cắt nửa đường tròn tại D. Gọi H là giao điểm của AE và đường thẳng d.

a) Chứng minh tứ giác BMHE nội tiếp đường tròn.

b) Chứng minh ba điểm B, D, H thẳng hàng.

Hướng dẫn giải

Hình vẽ minh họa

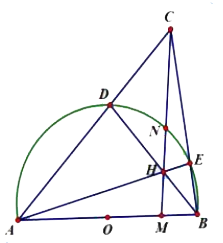
a) Ta có:  (giả thiết)

(góc nột tiếp chắn nửa đường tròn)

Xét tứ giác HEBM ta có  ở vị trí đối nhau và

Vậy tứ giác HEBM nội tiếp đường tròn.

b) Xét tam giác CAB có AE ⊥ CB nên AE là đường cao trong tam giác CAB.

CA ⊥ BD (góc nội tiếp chắn nửa đường tròn)

=> BD là đường cao trong tam giác CAB

Ta có BD giao với AE tại H nên H là trực tâm của tam giác CAB.

Vậy B, H, D thẳng hàng.

Ví dụ 2: Cho nửa đường tròn tâm O, đường kính AB. Lấy điểm C trên đoạn thẳng OA (C khác O và C khác A). Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn tại K. Gọi M là điểm bất kì trên cung BK (M khác B và K). Đường thẳng CK cắt các đường thẳng AM, BM lần lượt tại H và D. Đường thẳng BH cắt nửa đường tròn tại điểm thứ hai là N. Chứng minh ba điểm A, N, D thẳng hàng và tiếp tuyến tại N của nửa đường tròn đi qua trung điểm của HD.

Hướng dẫn giải

Hình vẽ minh họa:

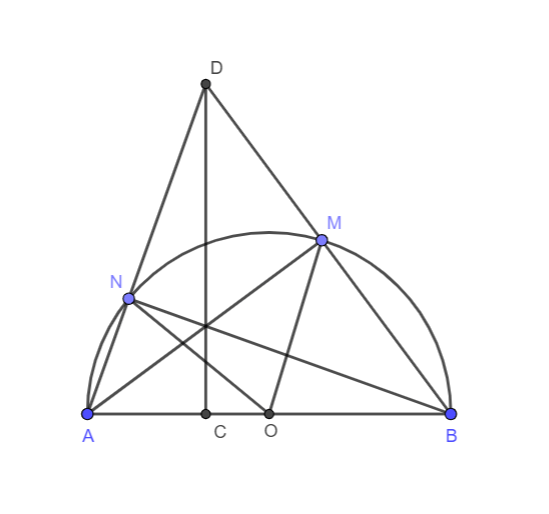
a) Chứng minh AN ⊥ BN từ giả thiết N ∈ (O) đường kính AB.

Chứng minh AD ⊥ BN:

Chỉ ra AM, DC là hai đường cao của tam giác ABD, AM ∩ DC = {H} nên H là trực tâm của tam giác ABD

=> AD ⊥ BH hay AD ⊥ BN

=> Ba điểm A, N, D thẳng hàng.

b) Gọi I là trung điểm cuả DH. Chỉ ra tam giác DHN vuông tại N là có NI là trung tuyến

=> NI = DH/2 = DI (tính chất trung tuyến của tam giác vuông)

=> Tam giác IDN cân tại I =>

Chỉ ra tam giác OAN cân tại O =>

=>

Xét tam giác ACD vuông tại C nên

=> IN ⊥ ON

Mà ON là bán kính của (O) nên IN là tiếp tuyến của (O) hay tiếp tuyến N của (O) đi qua I là trung điểm của DH.

C. Bài tập tự luyện chứng minh ba điểm thẳng hàng

Bài tập 1: Cho tam giác ABC vuông tại A. Đường tròn đường kính AB cắt BC tại D khác B. Gọi M là điểm bất kì trên đoạn AD. Kẻ MH, MI lần lượt vuông góc với AB, AC tại H, I. Kẻ HK vuông góc với ID tại K. Chứng minh và tứ giác AIKM nội tiếp, từ đó chứng minh ba điểm K, M, B thẳng hàng.

Bài tập 2: Cho tam giác ABC vuông tại A. Lấy B làm tâm, vẽ đường tròn bán kính BA, lấy điểm C làm tâm, vẽ đường tròn bán kính AC. Hai đường tròn này cắt nhau tại điểm thứ hai là D. Vẽ AM và AN lần lượt là các dây cung của đường tròn (B) và (C) sao cho AM vuông góc với AN và D nằm giữa M và N. Chứng minh ba điểm M, D, N thẳng hàng.

Bài tập 3: Cho nửa đường tròn (O; R) đường kính AB. Gọi C là điểm bất kì thuộc nửa đường tròn sao cho 0 < AC < BC. Gọi D là điểm thuộc cung nhỏ BC sao cho . Gọi E là giao điểm của AD và BC, F là giao điểm của AC và BD. Gọi I la trung điểm của EF. Chứng minh IC là tiếp tuyến của (O).

Bài tập 4: Cho hình thang ABCD có AB//CD. Gọi O là giao điểm của hai đường chéo AC vàBD. Gọi M, N, P lần lượt là trung điểm của AB, BC, AD. Gọi E là trung điểm của PN.Chứng minh rằng ba điểm M, O, E thẳng hàng.

Bài tập 5: Cho tam giác ABC nhọn nội tiếp đường tròn (O). Điểm M bất kỳ trên cung nhỏBC. Gọi E, F thứ tự là các điểm đối xứng của M qua AB, AC. Gọi H là trực tâm tam giácABC. Chứng minh rằng E, H, F thẳng hàng.

-------------------------------------