Chứng Minh định Lí Talet Thuận. - Hoc24

HOC24

Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng

• Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn

Đóng Đăng nhập Đăng ký

Lớp học

• Lớp 12
• Lớp 11
• Lớp 10
• Lớp 9
• Lớp 8
• Lớp 7
• Lớp 6
• Lớp 5
• Lớp 4
• Lớp 3
• Lớp 2
• Lớp 1

Môn học

• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Đạo đức
• Tự nhiên và xã hội
• Khoa học
• Lịch sử và Địa lý
• Tiếng việt
• Khoa học tự nhiên
• Hoạt động trải nghiệm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Chủ đề / Chương

Bài học

HOC24

Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng

• Tất cả
• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Hãy tham gia nhóm Học sinh Hoc24OLM Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài

Câu hỏi

Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay Đào Đức Mạnh 26 tháng 8 2015 lúc 18:54

Chứng minh định lí Talet thuận.

Lớp 5 Toán Những câu hỏi liên quan

• Pham Quang Truong

14 tháng 6 2015 lúc 9:41

chứng minh định lí Xê-va và định lí Meelenauyet bằng đinh lí talet với

Xem chi tiết Lớp 8 Toán Câu hỏi của OLM 0 0 Gửi Hủy

• Nguyen Nguyen

1 tháng 4 2020 lúc 15:13

Câu1: phát biểu và chứng minh định lý thuận của Talet, vẽ hình ghi giả thiết - kết luận và chứng minh định lý vừa nêu.

Xem chi tiết Lớp 8 Toán Bài 1: Định lý Talet trong tam giác 1 0 Gửi Hủy Trần Quốc Khanh 1 tháng 4 2020 lúc 15:25

Cho tgiac ABC với MN//BC, M,N thuộc AB,AC

Kẻ \(BH\perp AC\), ta có: \(\frac{S_{ANB}}{S_{ABC}}=\frac{\frac{1}{2}BH.AN}{\frac{1}{2}BH.AC}=\frac{AN}{AC}\left(1\right)\)

Tương tự ta cũng có: \(\frac{S_{AMC}}{S_{ABC}}=\frac{AM}{AB}\left(2\right)\)

Ta cần CM (1)=(2)

Ta có: \(S_{ANB}=S_{AMN}+S_{MNB}\left(3\right)\)

\(S_{AMC}=S_{AMN}+S_{MNC}\left(4\right)\)

Mà MN//BC nên : \(S_{MNB}=S_{MNC}\Rightarrow\left(3\right)=\left(4\right)\)

Từ đó có: \(S_{ANB}=S_{AMC}\Rightarrow\left(1\right)=\left(2\right)\Rightarrow\frac{AN}{AC}=\frac{AM}{AB}\)

A B C M N

Đúng 0 Bình luận (0) Khách vãng lai đã xóa Gửi Hủy

• Trần thị thùy dương

10 tháng 3 2022 lúc 1:58

Định lí talet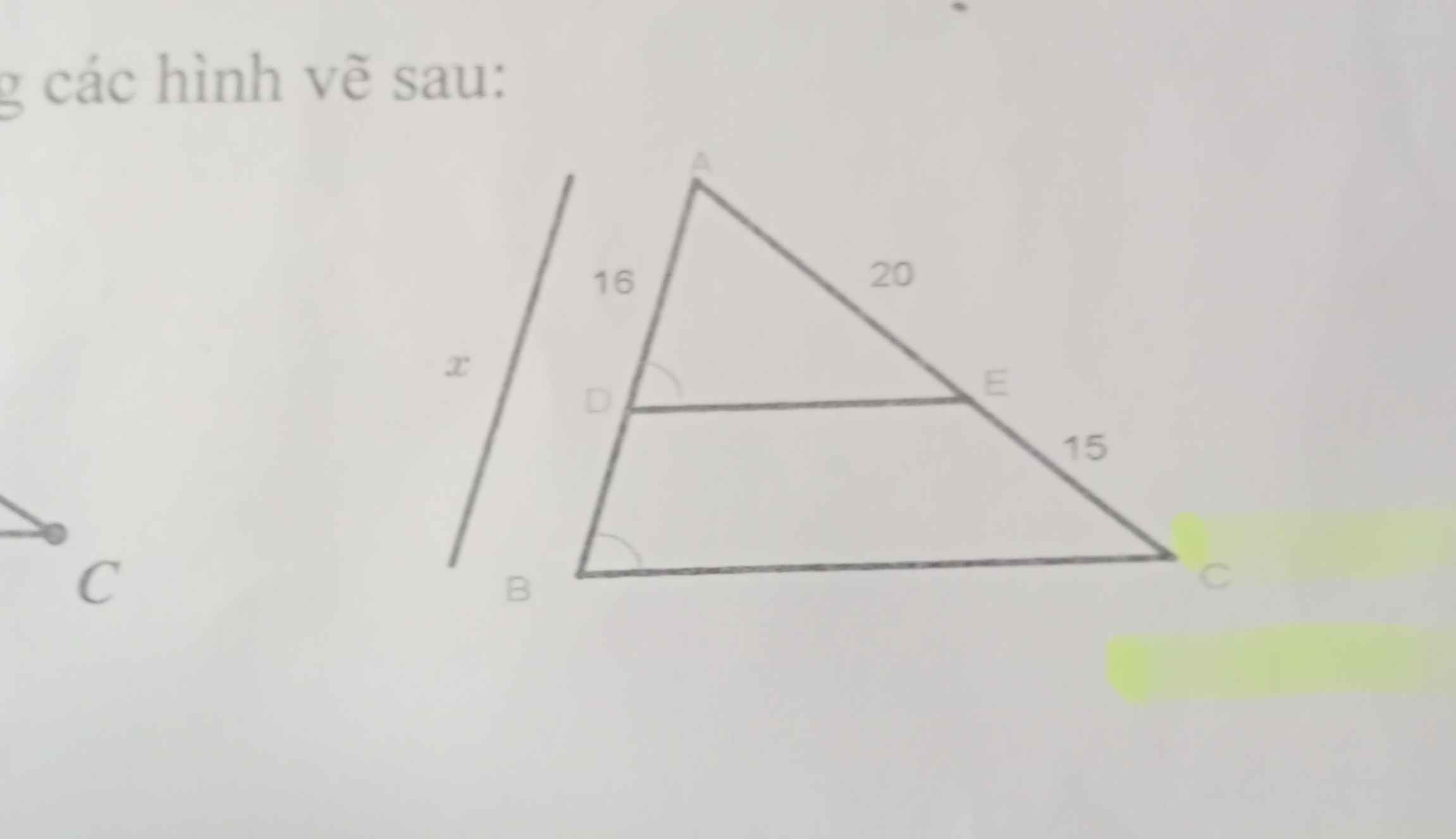

Xem chi tiết Lớp 8 Toán 1 0 Gửi Hủy Đỗ Tuệ Lâm 10 tháng 3 2022 lúc 6:36

Áp dụng đl ta-lét vào tam giác ABC có DE//BC có:

\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)

hay \(\dfrac{16}{DB}=\dfrac{20}{15}\Rightarrow DB=16:\dfrac{20}{15}=12\)

\(\Rightarrow x=AD+DB=16+12=28\)

Đúng 0 Bình luận (0) Gửi Hủy

• Hà Ánh Dương

23 tháng 12 2021 lúc 20:01

Một số định lí của những toán học nào từ thời cổ đại cụ thể được cho là còn phổ biến đến ngày nay?A. Talet, Pitago, ƠclitB. PitagoC. Talet, HômeD. Hôme

Xem chi tiết Lớp 6 Lịch sử 2 0 Gửi Hủy Lê Minh Đức 23 tháng 12 2021 lúc 20:01

A

Đúng 1 Bình luận (0) Gửi Hủy hoàng thị thanh hoa 23 tháng 12 2021 lúc 20:02

A

Đúng 0 Bình luận (0) Gửi Hủy

• Pham Trong Bach

6 tháng 4 2018 lúc 13:01

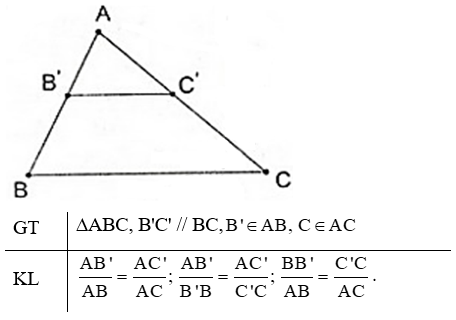
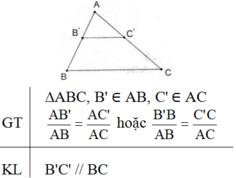
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Talet đảo.

Xem chi tiết Lớp 8 Toán 1 0 Gửi Hủy Cao Minh Tâm 6 tháng 4 2018 lúc 13:02

Định lí Talet đảo:

Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

 

Đúng 0 Bình luận (0) Gửi Hủy

• CP Enderboy

28 tháng 2 2020 lúc 16:58

Câu 1: Phát biểu định lí Talet thuận, đảo. Giả thiết, kết luận, vẽ hình

Câu 2: Phát biểu định lí đảo và hệ quả của định lí Talet. Vẽ hình, viết giả thiết, kết luận

Xem chi tiết Lớp 8 Toán Bài 1: Định lý Talet trong tam giác 1 0 Gửi Hủy Trúc Giang 28 tháng 2 2020 lúc 17:09

Câu 1:

*Định lí Ta - lét thuận: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

*Định lí Ta - lét đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Câu 2:

*Định lí Ta - lét đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Hệ quả của định lí Talet

Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.

Đúng 0 Bình luận (0) Khách vãng lai đã xóa Gửi Hủy

• Pham Trong Bach

5 tháng 6 2017 lúc 5:36

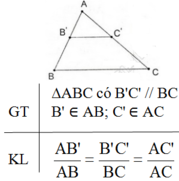
Phát biểu, vẽ hình, ghi giả thiết và kết luận của định lí Talet trong tam giác.

Xem chi tiết Lớp 8 Toán 1 0 Gửi Hủy Cao Minh Tâm 5 tháng 6 2017 lúc 5:38

Định lí Talet trong tam giác:

Nếu một đường thẳng song song với một cạnh của một tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.

 

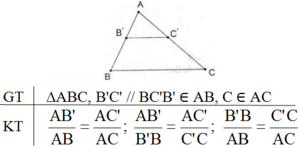
Đúng 0 Bình luận (0) Gửi Hủy

• Pham Trong Bach

28 tháng 8 2019 lúc 17:36

Phát biểu, vẽ hình, ghi giả thiết và kết luận về hệ quả của định lí Talet.

Xem chi tiết Lớp 8 Toán 1 0 Gửi Hủy Cao Minh Tâm 28 tháng 8 2019 lúc 17:37

Hệ quả của định lí Talet:

Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng với tỉ lệ ba cạnh của tam giác đã cho.

Đúng 0 Bình luận (0) Gửi Hủy

• Lê Ngọc Phương Trang

13 tháng 6 2020 lúc 11:17

Kết bạn zdới mình đêiiiiii ~~

À bạn nào giải thích giùm mình hệ quả định lí Talet với ạ không hiểu lắm nên không làm bài tập được :(

cho Vd

Xem chi tiết Lớp 8 Toán Câu hỏi của OLM 0 0 Gửi Hủy

Khoá học trên OLM (olm.vn)

• Toán lớp 5
• Tiếng Việt lớp 5
• Tiếng Anh lớp 5
• Khoa học lớp 5
• Lập trình Scratch