Chứng Minh Tứ Giác Là Hình Bình Hành, Hình Thoi, Hình Chữ Nhật, Hình ...

Trang chủ » Các Cách Chứng Minh Tứ Giác Là Hình Chữ Nhật » Chứng Minh Tứ Giác Là Hình Bình Hành, Hình Thoi, Hình Chữ Nhật, Hình ...

Có thể bạn quan tâm

Chứng minh hình bình hành, chứng minh hình thoi

  • A. Dấu hiệu nhận biết hình bình hành
  • B. Dấu hiệu nhận biết hình chữ nhật
  • C. Dấu hiệu nhận biết hình thoi
  • D. Dấu hiệu nhận biết hình vuông
  • E. Bài tập chứng minh tứ giác đã cho là hình bình hành, hình thoi, hình chữ nhật, hình vuông.

Bài tập Toán 9: Chứng minh tứ giác là hình bình hành, chứng minh tứ giác là hình thoi là một dạng toán khó thường gặp trong đề thi tuyển sinh vào lớp 10 môn Toán. Tài liệu được  GiaiToan.com biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.

A. Dấu hiệu nhận biết hình bình hành

+ Tứ giác có các cạnh đối song song là hình bình hành.

+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.

+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

+ Tứ giác có các góc đối bằng nhau là hình bình hành.

+ Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

B. Dấu hiệu nhận biết hình chữ nhật

+ Tứ giác có ba góc vuông là hình chữ nhật.

+ Hình thang cân có một góc vuông là hình chữ nhật.

+ Hình bình hành có một góc vuông là hình chữ nhật.

+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

C. Dấu hiệu nhận biết hình thoi

+ Tứ giác có bốn cạnh bằng nhau là hình thoi.

+ Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

+ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

D. Dấu hiệu nhận biết hình vuông

+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

+ Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.

+ Hình thoi có một góc vuông là hình vuông.

+ Hình thoi có hai đường chéo bằng nhau là hình vuông.

E. Bài tập chứng minh tứ giác đã cho là hình bình hành, hình thoi, hình chữ nhật, hình vuông.

Ví dụ 1: Cho đường tròn tâm (O) ngoại tiếp tam giác nhọn ABC. Gọi M, N lần lượt là điểm chính giữa cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại H và K. Chứng minh tứ giác BHIK là hình thoi.

Hướng dẫn giải

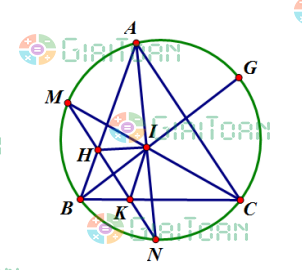
Chứng minh tứ giác là hình bình hành, hình thoi, hình chữ nhật, hình vuông

Tứ giác CNIK nội tiếp suy ra

\widehat {IKC} = \widehat {INC} (Hai góc nội tiếp chắn cung IC)

\widehat {ABC} = \widehat {ANC} (Hai góc nội tiếp chắn cung AC)

\Rightarrow \widehat {ABC} = \widehat {IKC}

Do hai góc ở vị trí đồng vị => IK // HB

Gọi BI cắt (O) tại G. Vì I là giao điểm của ba đường phân giác của tam giác ABC nên G là điểm chính giữa cung AC và BI là phân giác ABC.

Chứng minh tương tự AMHI nội tiếp

=> \widehat {AHI} = \widehat {AMI} (Hai góc nội tiếp chắn cung AI)

\Rightarrow \widehat {ABC} = \widehat {AHI}

Do hai góc ở vị trí đồng vị => HI // BK

Xét tứ giác BHIK có:

IK // BH (cmt)

HI // BK (cmt)

=> BHIK là hình bình hành. Mà BI là tia phân giác của HBK.

=> BHIK là hình thoi.

Ví dụ 2: Cho đường tròn (O) bán kính R có hai đường kính AB và CD vuông góc với nhau. Trên đoạn thẳng AB lấy điểm M (M khác O). CM cắt (O) tại N. Đường thẳng vuông góc với AB tại M cắt tiếp tuyến tại N của đường tròn ở P. Chứng minh:

a) Tứ giác OMNP nội tiếp.

b) Tứ giác CMPO là hình bình hành.

Hướng dẫn giải

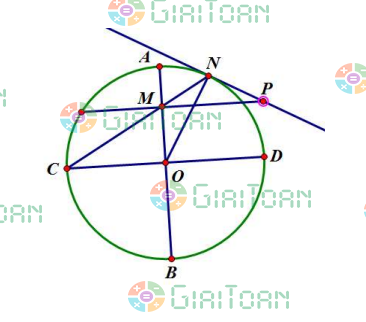
Chứng minh tứ giác là hình bình hành, hình thoi, hình chữ nhật, hình vuông

a) Ta có \widehat {OMP} = {90^0} (vì PM vuông góc với AB)

\widehat {ONP} = {90^0} (Vì NP là tiếp tuyến)

Như vậy M và N cùng nhìn OP dưới một góc bằng 900

=> M và N cùng nằm trên đường tròn đường kính OP.

=> Tứ giác OMNP nội tiếp.

b) Tứ giác OMNP nội tiếp => \widehat {OPM} = \widehat {ONM} (Góc nội tiếp chắn cung OM)

Tam giác ONC cân tại O vì ON = OC = R => \widehat {ONC} = \widehat {OCN} \Rightarrow \widehat {OPM} = \widehat {OCM}

Xét hai tam giác OMC và tam giác MOP ta có:

\begin{matrix} \widehat {MOC} = \widehat {OMP} = {90^0} \hfill \\ \widehat {OPM} = \widehat {OCM} \Rightarrow \widehat {CMO} = \widehat {POM} \hfill \\ \end{matrix}

MO là cạnh chung

\Rightarrow \Delta OMC = \Delta MOP \Rightarrow OC = MP\left( 1 \right)

Theo giả thiết ta có: \left\{ {\begin{array}{*{20}{c}} {CD \bot AB} \\ {PM \bot AB} \end{array} \Rightarrow CO//PM\left( 2 \right)} \right.

Từ (1) và (2) => Tứ giác CMPO là hình bình hành.

Ví dụ 3: Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Kẻ tiếp tuyến AB với đường tròn (O) (B là tiếp điểm) và đường kính BC. Trên đoạn thẳng CO lấy điểm I (I khác C, I khác O). Đường thẳng IA cắt (O) tại hai điểm D và E (D nằm giữa A và E). Gọi H là trung điểm của đoạn thẳng DE. Tia CD cắt AO tại điểm P, tia EO cắt BP tại điểm F. Chứng minh tứ giác BECF là hình chữ nhật.

Hướng dẫn giải

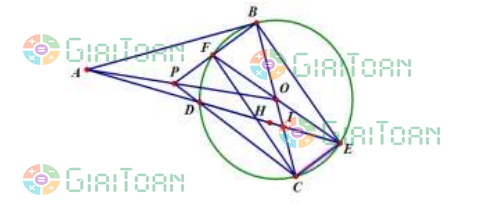
Chứng minh tứ giác là hình bình hành, hình thoi, hình chữ nhật, hình vuông

Gọi F’ là giao điểm của BP và đường tròn (O). Gọi QA là tiếp tuyến thứ 2 với đường tròn (O).

Vì tứ giác BDQC là tứ giác nội tiếp nên \widehat {QDC} = \widehat {QBC}\left( 1 \right).

Vì tứ giác ABOQ là tứ giác nội tiếp đường tròn đường kính AO nên \widehat {QBC} = \widehat {QAO}\left( 2 \right)

Từ (1) và (2) \Rightarrow \widehat {QDC} = \widehat {OAQ} => APDQ là tứ giác nội tiếp \Rightarrow \widehat {PAD} = \widehat {PQA}\left( 3 \right)

Ta có: \widehat {PDA} = \widehat {EDC} = \widehat {EBC}\left( 4 \right)

Ta có: \Delta ABP = \Delta AQP\left( {c - g - c} \right) \Rightarrow \widehat {PQA} = \widehat {PBA}\left( 5 \right)

Từ (3), (4), (5)

\begin{matrix} \Rightarrow \widehat {PBA} = \widehat {EBC} \hfill \\ \Rightarrow \widehat {PBE} = \widehat {ABC} = {90^0} \hfill \\ \Rightarrow \widehat {F'BE} = {90^0} \hfill \\ \end{matrix}

=> F’E là đường kính của (O) => F’ ∈ OE => F’ ≡ F

Vì FBEC là tứ giác nội tiếp nên \widehat {FCE} = {180^0} - \widehat {FBL} = {90^0}

Tứ giác FBEC có: \widehat {FCE} = \widehat {FBE} = \widehat {BCE} = {90^0} nên là hình chữ nhật.

-----------------------------------------------------

Hy vọng tài liệu Chuyên đề Toán 9: Chứng minh tứ giác sẽ giúp ích cho các bạn học sinh học nắm chắc các cách biến đổi hệ phương trình đồng thời học tốt môn Toán lớp 9. Chúc các bạn học tốt, mời các bạn tham khảo!

Từ khóa » Các Cách Chứng Minh Tứ Giác Là Hình Chữ Nhật