Chương I: Bài Tập Thời Gian Trong Dao động điều Hòa - SoanBai123

Chương I: Bài tập thời gian trong dao động điều hòa

Chương I: Bài tập số lần đi qua vị trí li độ x cho trước trong dao động điều hòa

Thời gian trong dao động điều hòa. Các dạng Bài tập thời gian trong dao động điều hòa. Phương pháp giải các Bài tập về thời gian trong dao động điều hòa chương trình vật lý 12 ôn thi Quốc gia.

Xác định thời gian đi từ vị trí x1 đến vị trí x2 Sử dụng kiến thức liên hệ giữa dao động điều hòa và chuyển động tròn đều xác định thời gian

t=Δφω=T.Δφ2πt=Δφω=T.Δφ2π​

Trong đó:

• Δφ: là góc mà vật quét được khi chuyển động từ x1 đến x2
• ω: tần số góc (rad/s); T: chu kỳ dao động (s)

Bài tập 1: Một chất điểm dao động điều hoà với biên độ 10 (cm) và tần số góc 10 (rad/s). Khoảng thời gian ngắn nhất để nó đi từ vị trí có li độ +3,5 cm đến vị trí cân bằng là A. 0,036 s. B. 0,121 s. C. 2,049 s. D. 6,951 s.

Hướng dẫn

Chương I: Bài tập thời gian trong dao động điều hòa

sinΔφ=0,35 => Δφ = 0, 3576(rad) => t = 0,036(s)

Bài tập 2: Vật dao động điều hoà, thời gian ngắn nhất vật đi từ vị trí x=+A đến vị trí x = A/3 là 0,1 s. Chu kì dao động của vật là A. 1,85 s. B. 1,2 s. C. 0,51 s. D. 0,4 s.

Hướng dẫn

cosΔφ=1/3 => Δφ=70,53 t=T.Δφ2πt=T.Δφ2π => T=0,51s

Bài tập 3: Vật dao động điều hoà với biên độ A. Thời gian ngắn nhất vật đi từ vị trí có li độ A/2 đến vị trí có li độ A là 0,2 s. Chu kì dao động của vật là: A.0,12 s. B. 0,4 s. C. 0,8 s. D. 1,2 s.

Hướng dẫn

Δφ = 60 t=T.Δφ2πt=T.Δφ2π => T=1,2s

Bài tập 4: Một chất điểm dao động điều hòa với chu kì 1 s với biên độ 4,5 cm. Khoảng thời gian trong một chu kỳ để vật cách vị trí cân bằng một khoảng nhỏ hơn 2 cm là A. 0,29 s. B. 16,80 s. C. 0,71 s. D. 0,15 s.

Hướng dẫn

Δφ = 52,77 t=2T.Δφ2πt=2T.Δφ2π = 0,29

Bài tập 5: Một chất điểm dao động điều hòa với chu kì T. Khoảng thời gian trong một chu kỳ để vật cách vị trí cân bằng một khoảng lớn hơn nửa biên độ là A. T/3. B. 2T/3. C. T/6. D. T/2.

Hướng dẫn

t=4.T/6=2T/3 Biết mối quan hệ giữ t1; t2 xác định các đại lượng T, A, x1 …

Bài tập 6 : Một dao động điều hoà có chu kì dao động là T và biên độ là A. Tại thời điểm ban đầu vật có li độ x1 > 0. Thời gian ngắn nhất để vật đi từ vị trí ban đầu về vị trí cân bằng gấp ba thời gian ngắn nhất để vật đi từ vị trí ban đầu về vị trí biên x = +A. Chọn phương án đúng. A. x1=0,924A. B. x1=0,5√3A. C. x1=0,5A√2. D. x1=0,021A.

Hướng dẫn

t1 + t=T/4 t1=3t2 x1=Acos2πt2Tx1=Acos2πt2T => x1=0,924A

Bài tập 7: Một dao động điều hoà có chu kì dao động là T và biên độ là A. Tại thời điểm ban đầu vật có li độ x1 (mà x1 ≠0; x1 ≠ ±A), bất kể vật đi theo hướng nào thì cứ sau khoảng thời gian ngắn nhất Δt nhất định vật lại cách vị trí cân bằng một khoảng như cũ. Chọn phương án đúng.

Hướng dẫn

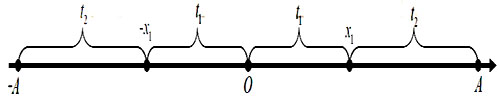Δt=2t1 = 2t2 mà t1 + t2 = T/4 nên t1 = t2 = T/8. x1=Asin2πt1Tx1=Asin2πt1T=0,5A√2 Trục phân bố thời gian khi chất điểm chuyển động giữa các vị trí đặc biệt

Bài tập 8: Một vật dao động điều hoà có phương trình li độ x=8cos(7πt + π/6) cm. Khoảng thời gian tối thiểu để vật đi từ li độ 4√2cm đến vị trí có li độ -4√3cm là A. 1/24 s. B. 5/12 s. C. 1/6 s. D. 1/12 s.

Hướng dẫn

A=8cm => 4√2=A/√2; -4√3=-A√3/2 => t=7T/24=1/12(s)

Bài tập 9: Một dao động điều hoà có chu kì dao động là T và biên độ là A. Thời gian ngắn nhất để vật đi từ điểm có li độ cực đại về điểm có li độ bằng một nửa biên độ cực đại mà véctơ vận tốc có hướng cùng với hướng của trục toạ độ là A. T/3. B. 5T/6. C. 2T/3. D. T/6.

Hướng dẫn

t=5T/6

Bài tập 10: Một con lắc lò xo đang dao động điều hòa với biên độ A, thời gian ngắn nhất để con lắc di chuyển từ vị trí có li độ x1=‒ A đến vị trí có li độ x2=A/2 là 1 s. Chu kì dao động của con lắc là: A. 6 s. B. 1/3 s. C. 2 s. D. 3 s.

Hướng dẫn

t=T/3=1 => T=3(s) Li độ và vận tốc tại các điểm đặc biệt sau các khoảng thời gian bằng nhau Sau khoảng thời gian bằng nhau Δt=T/6 vật chuyển động đến các vị trí M hoặc O, hoặc N. 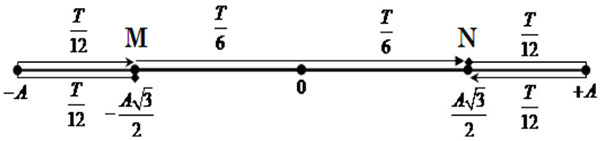Sau khoảng thời gian bằng nhau Δt=T/8 vật chuyển động đến các vị trí M1, M2, O, M3, M4 Sau khoảng thời gian bằng nhau Δt=T/12 vật chuyển động đến các vị trí M1, M2, M3, M4 (O); M5, M6, M7

Bài tập 11: Một chất điểm đang dao động điều hoà trên một đoạn thẳng xung quanh vị trí cân bằng O. Gọi M, N là hai điểm trên đường thẳng cùng cách đều O. Biết cứ 0,05 s thì chất điểm lại đi qua các điểm M, O, N và tốc độ của nó lúc đi qua các điểm M, N là 20π cm/s. Biên độ A bằng A. 4 cm. B. 6 cm. C. 4√2cm. D. 4√3cm.

Hướng dẫn

T/6=0,05 => T=0,3(s) => ω=20π/3 (rad/s) |xM|=A√3/2 => |vM|=Aω/2 => A=6cm

Bài tập 12: Một chất điểm đang dao động điều hoà trên một đoạn thẳng. Trên đoạn thẳng đó có bảy điểm theo đúng thứ tự M1, M2, M3, M4, M5, M6 và M7 với M4 là vị trí cân bằng. Biết cứ 0,05 s thì chất điểm lại đi qua các điểm M1, M 2, M3, M4, M5, M6 và M7. Tốc độ của nó lúc đi qua điểm M3 là 20π cm/s. Biên độ A bằng A. 4 cm. B. 6 cm. C. 12 cm. D. 4√3 cm.

Hướng dẫn

T/12=0,05 => T=0,6(s) => ω=20π/6 |xM|=A/2 => |vM|=Aω√3/2 => A=4√3cm

Bài tập 13: Vật đang dao động điều hòa dọc theo đường thẳng. Một điểm M nằm cố định trên đường thẳng đó, phía ngoài khoảng chuyển động của vật, tại thời điểm t thì vật xa điểm M nhất, sau đó một khoảng thời gian ngắn nhất là Δt thì vật gần điểm M nhất. Độ lớn vận tốc của vật sẽ bằng nửa vận tốc cực đại vào thời điểm gần nhất là A. t + Δt/3 B. t + Δt/6 C. t + Δt/4 D. 0,5t + 0,25Δt

Hướng dẫn

Δt=T/2 =>T =2Δt v=vmax/2=Aω/2 thay vào phương trình độc lập với thời gian => x=A√3/2 Thời gian ngắn nhất để đi từ A đến A√3/2 là T/12 => thời điểm cần tìm: t + T/12=t + Δt/6 Bài toán thời gian liên quan đến vận tốc, động lượng Sử dụng biểu thức độc lập với thời gian

x2+v2ω2=A2x2+v2ω2=A2 => hệ phương tình​

theo vận tốc

• nếu v=v1 => x1
• nếu v=v2 => x2

theo động lượng p=mv

• nếu p=p1 => x1
• nếu p=p2 => x2

Trong 1 chu kỳ vật dao động điều hòa: vận tốc của vật trong đoạn [-x1; x1] là v1 x1=Asin(ωt1) => t1=1ωarcsinx1At1=1ωarcsinx1A x1=Acos(ωt2) => t2=1ωarccosx1At2=1ωarccosx1A

• v > v1 sẽ nằm trong đoạn [-x1; x1] thời gian tương ứng là 4t1
• v < v1 sẽ nằm ngoài đoạn [-x1; x1] thời gian tương ứng là 4t2

Bài tập 14: Một chất điểm dao động điều hòa với chu kì T trên trục Ox với O là vị trí cân bằng. Thời gian ngắn nhất vật đi từ điểm có toạ độ x=0 đến điểm mà tốc độ của vật bằng nửa tốc độ cực đại là A. T/8. B. T/16. C. T/6. D. T/12.

Hướng dẫn

v=vmax/2=Aω/2 thay vào phương trình độc lập với thời gian => x=A√3/2 Thời gian đi từ x=0 đến x=A√3/2 là Δt=T/6

Bài tập 15 : Một chất điểm dao động điều hòa với chu kì T. Khoảng thời gian trong một chu kỳ để vật có tốc độ nhỏ hơn 1/3 tốc độ cực đại là. A. T/3. B. 2T/3. C. 0,22T. D. 0,78T.

Hướng dẫn

v1=vmax/3=Aω/3 => x1=A√8/3 v < v1 => Δt=4t2=41ωarccosx1A1ωarccosx1A=0,22T

Bài tập 16 : Một chất điểm dao động điều hòa với chu kì T. Khoảng thời gian trong một chu kỳ để vật có tốc độ lớn hơn 0,5 tốc độ cực đại là A. T/3. B. 2T/3. C. T/6. D. T/2.

Hướng dẫn

v1=vmax/2=Aω/2 => x1=A√3/2 v > v1 => Δt=4t1 = 41ωarcsinx1A1ωarcsinx1A=2T/3

Bài tập 17: Một chất điểm dao động điều hòa với chu kì T. Gọi vtb là tốc độ trung bình của chất điểm trong một chu kì, v là tốc độ tức thời của chất điểm. Trong một chu kì, khoảng thời gian mà v ≥ 0,25πvtb là: A. T/3. B. 2T/3. C. T/6. D. T/2.

Hướng dẫn

vtb=s/t=4A/T=2Aω/π => 0,25πvtb = Aω/2 v1 = Aω/2 => x1=A√3/2 v > v1 => Δt=4t1 = 41ωarcsinx1A1ωarcsinx1A=2T/3

Bài tập 18 : Một vật nhỏ dao động điều hòa với chu kì T và biên độ 8 cm. Biết trong một chu kì, khoảng thời gian để vật nhỏ có độ lớn vận tốc không vượt quá 16 cm/s là T/3. Tần số góc dao động của vật là A. 4 rad/s. B. 3 rad/s. C. 2 rad/s. D. 5 rad/s.

Hướng dẫn

v < v1 => Δt=4t2 = T/3 => t2=T/12=π/(6ω) x1 = Acos(ωt2)=A√3/2=4√3 thay vào phương trình x2+v2ω2=A2x2+v2ω2=A2 => ω = 4 rad/s

Bài tập 19 : Một vật dao động điều hòa với biên độ 10 cm. Biết trong một chu kì, khoảng thời gian để tốc độ dao động không nhỏ hơn π (m/s) là 1/15 (s). Tần số góc dao động của vật có thể là : A. 6,48 rad/. B. 43,91 rad/s. C. 6,36 rad/s. D. 39,95 rad/s.

Hướng dẫn

v1 = π(m/s)=100π (cm/s) => v > v1 => Δt=4t1 = 1/15 => t1 = 1/60 (s) => x1=10sin(ω/60) thay vào phương trình x2+v2ω2=A2x2+v2ω2=A2 => ω=39,95 rad/s.

Bài tập 20: Con lắc lò xo gồm một vật nhỏ có khối lượng 250 g và lò xo nhẹ có độ cứng 100 N/m dao động điều hòa dọc theo trục Ox với biên độ 4 cm. Khoảng thời gian ngắn nhất để vận tốc của vật có giá trị từ ‒40 cm/s đến 40√3 cm/s là A. π/40 (s). B. π/120 (s). C. π/20 (s). D. π/60 (s)

Hướng dẫn

ω=√kmω=km=20(rad/s) v1=-40cm/s => x1=-A√3/2 v2=40√3 cm/s => x2=-A/2

Bài toán thời gian liên quan đến gia tốc, năng lượng, lực trong dao động điều hòa

• Vận dụng công thức tính gia tốc a=-ω2x
• Công thức tính độ lớn lực phục hồi: F=kx

Trong 1 chu kỳ vật dao động điều hòa: gia tốc của vật trong đoạn [-x1; x1] là |a1| x1=Asin(ωt1) => t1=1ωarcsinx1At1=1ωarcsinx1A x1=Acos(ωt2) => t2=1ωarccosx1At2=1ωarccosx1A

• |a| < |a1| sẽ nằm trong đoạn [-x1; x1] thời gian tương ứng là 4t1
• |a| > |a1|sẽ nằm ngoài đoạn [-x1; x1] thời gian tương ứng là 4t2

Bài tập 21: Một vật dao động điều hòa với chu kì T, trên một đoạn thẳng, giữa hai điểm biên M và N. Chọn chiều dương từ M đến N, gốc tọa độ tại vị trí cân bằng O, mốc thời gian t=0 là lúc vật đi qua trung điểm I của đoạn MO theo chiều dương. Gia tốc của vật bằng không lần thứ nhất vào thời điểm A. T/8. B. T/16. C. T/6. D. T/12.

Hướng dẫn

A=OM => OI=A/2 => x1=-0,5A; a= 0=> x2=0 => Δt=T/12

Bài tập 22: Một con lắc lò xo dao động theo phương ngang. Lực đàn hồi cực đại tác dụng vào vật là 12 N. Khoảng thời gian giữa hai lần liên tiếp vật chịu tác dụng của lực kéo lò xo 6√3N là 0,1 (s). Chu kỳ dao động của vật là A. 0,4 (s). B. 0,3 (s). C. 0,6 (s). D. 0,1 (s).

Hướng dẫn

Fmax=kA; F= kx1 =>x1=A√3/2 Lực kéo => lò xo đang giãn => vật sẽ đi từ x1 ra biên rồi quay lại x1 => Δt=T/6=0,1 => T=0,6(s)

Bài tập 23: Vật dao động điều hòa với vận tốc cực đại bằng 3 m/s và gia tốc cực đại bằng 30π (m/s2). Lúc t=0 vật có vận tốc v1=+1,5 m/s và thế năng đang giảm. Hỏi sau thời gian ngắn nhất bao nhiêu thì vật có gia tốc bằng ‒15π (m/s2)? A. 0,05 s. B. 0,15 s. C. 0,10 s. D. 1/12 s.

Hướng dẫn

vmax = ωA; amax = ω2A => ω=10π (rad/s) v1=+1,5 m/s=vmax/2 và thế năng đang giảm => x1=-A√3/2 a2=-15π => x2=A/2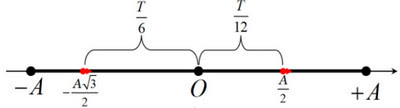 => Δt=T/4 = 0,05 s

Bài tập 24: Một con lắc lò xo dao động điều hòa với chu kì π/2 (s), tốc độ cực đại của vật là 40 (cm/s). Tính thời gian trong một chu kì gia tốc của vật không nhỏ hơn 96 (cm/s2). A. 0,78 s. B. 0,71 s. C. 0,87 s. D. 0,93 s

Hướng dẫn

ω= 2π/T=4 (rad/s); vmax=Aω => A=10(cm) |a1|=96 => x1=6 (cm) |a| > |a1| => Δt=4t2 = 41ωarccosx1A1ωarccosx1A=0,93s

Bài tập 25: Một chất điểm dao động điều hòa với chu kì T. Khoảng thời gian trong một chu kỳ để vật có độ lớn gia tốc bé hơn 1/2 gia tốc cực đại là A. T/3. B. 2T/3. C. T/6. D. T/2.

Hướng dẫn

|a1|=ω2A/2 => x1=A/2 (cm) |a| < |a1| => Δt=4t1 = 41ωarcsinx1A1ωarcsinx1A=T/3

Bài tập 26: Một con lắc lò xo dao động điều hòa với chu kì T và biên độ 5 cm. Biết trong một chu kì, khoảng thời gian để vật nhỏ của con lắc có độ lớn gia tốc không vượt quá 100 cm/s2 là T/3. Lấy π2=10. Tần số dao động của vật là A. 4 Hz. B. 3 Hz. C. 2 Hz. D. 1 Hz.

Hướng dẫn

|a1|=100 cm/s2 |a| < |a1| => Δt=4t1 = T/3 => t1 = T/12 => x1=Asin(ωt1)=2,5cm => ω=√|a1||x1|ω=|a1||x1|=2π => f=1Hz

Bài tập 27: Một vật dao động điều hòa với tần số 2 Hz. Tính thời gian trong một chu kì Wt ≤ 2Wđ. A. 0,196 s. B. 0,146 s. C. 0,096 s. D. 0,304 s.

Hướng dẫn

Wt=2Wđ => 3Wt = W => x1 = A√23A23 Wt ≤ 2Wđ nằm trong đoạn [-x1; x1] => Δt=4t1=41ωarcsinx1A1ωarcsinx1A=0,304 s. Chuyên mục: Bài Tập Vật Lý Lớp 12

Thảo luận cho bài: Chương I: Bài tập thời gian trong dao động điều hòa

Bài viết cùng chuyên mục

• Chương VII: Bài tập phóng xạ, vật lý hạt nhân

• Chương VII: Bài tập năng lượng hạt nhân

• Chương VII: Bài tập cấu tạo hạt nhân, thuyết tương đối

• Chương VI: Bài tập tia x, lượng tử ánh sáng

• Chương VI: Bài tập tiên đề Bo, vật lý lượng tử

• Chương VI: Bài tập lượng tử ánh sáng pin quang điện, chuyển động của e trong điện trường, từ trường

• Chương VI: Bài tập lượng tử ánh sáng, các định luật quang điện

• Chương V: Bài tập vật giao thoa hỗn hợp ánh sáng, giao thoa ánh sáng trắng