Chuyên đề Hàm Số Lượng Giác - Toán Lớp 10 - Trường Quốc Học
Có thể bạn quan tâm
Chuyên đề Hàm số lượng giác lớp 10 bao gồm kiến thức lý thuyết lượng giác cần nhớ và các bài tập tự giải.
A. Kiến thức cần nhớ
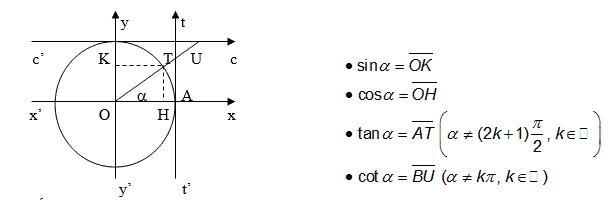
1. Các hằng đẳng thức cơ bản
a) $ {{\sin }^{2}}x+{{\cos }^{2}}x=1$
b) $ \tan x=\frac{{\sin x}}{{\cos x}}$
c) $ \cot x=\frac{{\cos x}}{{\sin x}}$
d) $ 1+{{\tan }^{2}}x=\frac{1}{{{{{\cos }}^{2}}x}}$
e) $ 1+{{\cot }^{2}}x=\frac{1}{{{{{\sin }}^{2}}x}}$ f) $ \tan x.\cot x=1$
2. Giá trị của các hàm lượng giác cung liên quan đặc biệt
a) Hai cung đối nhau
$ \begin{array}{l}\cos (-x)=\cos x\\\sin (-x)=-\sin x\\\tan (-x)=-\tan x\\\cot (-x)=-\cot x\end{array}$
b) Hai cung bù nhau
$ \begin{array}{l}\sin (\pi -x)=\sin x\\\cos (\pi -x)=-\cos x\\\tan (\pi -x)=-\tan x\\\cot (\pi -x)=-\cot x\end{array}$
c) Hai cung khác nhau
$ \begin{array}{l}\sin (x+2\pi )=\sin x\\\cos (x+2\pi )=\cos x\\\tan (x+2\pi )=\tan x\\\cot (x+2\pi )=\cot x\end{array}$
d) Hai cung khác nhau
$ \begin{array}{l}\sin (\pi +x)=-\sin x\\\cos (\pi +x)=-\cos x\\\tan (\pi +x)=\tan x\\\cot (\pi +x)=\cot x\end{array}$
e) Hai cung phụ nhau
$ \begin{array}{l}\sin \left( {\frac{\pi }{2}-x} \right)=\cos x\text{ };\text{ }\cos \left( {\frac{\pi }{2}-x} \right)=\sin x\\\tan \left( {\frac{\pi }{2}-x} \right)=\cot x\text{ ; }\cot \left( {\frac{\pi }{2}-x} \right)=\tan x\end{array}$
B. Bài tập
1. Tìm các giá trị của $ \alpha $để biểu thức sau đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
$ A=\frac{1}{{1+\sin \alpha }}\text{ ; }B=\frac{1}{{1-\cos \alpha }}$
2. Xét dấu của các biểu thức sau:
a) $ \sin {{123}^{o}}-\sin {{132}^{o}}$
b) $ \cot {{304}^{o}}-\cot {{316}^{o}}$
3. Rút gọn các biểu thức sau:
a) $ 5\tan {{540}^{o}}+2\cos {{1170}^{o}}+4\sin {{990}^{o}}-3\cos {{540}^{o}}$
b) $ 3\sin \frac{{25\pi }}{6}-3\tan \frac{{13\pi }}{4}+2\cos \frac{{19\pi }}{3}$
c) $ {{\sin }^{2}}{{15}^{o}}+{{\sin }^{2}}{{35}^{o}}+{{\sin }^{2}}{{55}^{o}}+{{\sin }^{2}}{{75}^{o}}$
d) $ {{\cos }^{2}}{{15}^{o}}+{{\cos }^{2}}{{35}^{o}}+{{\cos }^{2}}{{55}^{o}}+{{\cos }^{2}}{{75}^{o}}$
e) $ {{\sin }^{2}}\frac{\pi }{{12}}+{{\sin }^{2}}\frac{{3\pi }}{{12}}+{{\sin }^{2}}\frac{{5\pi }}{{12}}+{{\sin }^{2}}\frac{{7\pi }}{{12}}+{{\sin }^{2}}\frac{{9\pi }}{{12}}+{{\sin }^{2}}\frac{{11\pi }}{{12}}$
f) $ {{\cos }^{2}}\frac{\pi }{{12}}+{{\cos }^{2}}\frac{{3\pi }}{{12}}+{{\cos }^{2}}\frac{{5\pi }}{{12}}+{{\cos }^{2}}\frac{{7\pi }}{{12}}+{{\cos }^{2}}\frac{{9\pi }}{{12}}+{{\cos }^{2}}\frac{{11\pi }}{{12}}$
g) $ \sin (\pi +a)-\cos \left( {\frac{\pi }{2}+a} \right)+\cot (2\pi -a)+\tan \left( {\frac{{3\pi }}{2}+a} \right)$
h) $ A={{\sin }^{4}}a+{{\cos }^{2}}a+{{\sin }^{2}}a.{{\cos }^{2}}a$
i) $ B=\frac{{{{{\left( {\sin \frac{a}{2}+\cos \frac{a}{2}} \right)}}^{2}}-1}}{{\tan \frac{a}{2}-\sin \frac{a}{2}.\cos \frac{a}{2}}}$
j) $ C=\frac{{{{{\cos }}^{2}}{{{696}}^{o}}+\tan (-{{{260}}^{o}}).\tan {{{530}}^{o}}-{{{\cos }}^{2}}156}}{{{{{\tan }}^{2}}{{{252}}^{o}}+{{{\cot }}^{2}}{{{342}}^{o}}}}$
k) $ {{\left[ {\tan \frac{{17\pi }}{4}+\tan \left( {\frac{{7\pi }}{2}-b} \right)} \right]}^{2}}+{{\left[ {\cot \frac{{13\pi }}{4}+\cot \left( {7\pi -b} \right)} \right]}^{2}}$
l) $ \left( {\sqrt{{\frac{{1-\sin x}}{{1+\sin x}}}}-\sqrt{{\frac{{1+\sin x}}{{1-\sin x}}}}} \right)\left( {\sqrt{{\frac{{1-\cos x}}{{1+\cos x}}}}-\sqrt{{\frac{{1+\cos x}}{{1-\cos x}}}}} \right)$
m) $ {{\sin }^{3}}a(1+\cot a)+{{\cos }^{3}}a(1+\tan a)$
n) $ \frac{{\tan b}}{{\tan b+\cot b}}$
o) $ \frac{{1-{{{\cos }}^{4}}a-{{{\sin }}^{4}}a}}{{{{{\cos }}^{4}}a}}$
p) $ \frac{{\sin (x-\pi ).\cos (x-2\pi ).\sin (2\pi -x)}}{{\sin \left( {\frac{\pi }{2}-x} \right).\cot (\pi -x).\cot \left( {\frac{{3\pi }}{2}+x} \right)}}$
q) $ {{\left[ {\sin \left( {\frac{\pi }{2}-x} \right)+\sin (\pi -x)} \right]}^{2}}+{{\left[ {\cos \left( {\frac{{3\pi }}{2}-x} \right)+\cos (2\pi -x)} \right]}^{2}}$
r) $ \sin \left( {\frac{\pi }{3}-a} \right).\tan \left( {\frac{{2\pi }}{3}+a} \right).\cos \left( {\frac{{5\pi }}{3}+a} \right)+\tan (\pi +a).\tan \left( {\frac{{3\pi }}{2}-a} \right)$
s) $ \frac{{\cot (5,5\pi -a)+\tan (b-4\pi )}}{{\cot (a-6\pi )-\tan (b-3,5\pi )}}$
t) $ \tan {{50}^{o}}.\tan {{190}^{o}}.\tan {{250}^{o}}.\tan {{260}^{o}}.\tan {{400}^{o}}.\tan {{700}^{o}}$
4. Cho A, B, C là ba góc của tam giác ABC. Chứng minh:
a) $ \sin (A+B)=\sin C\text{; cos(B}+\text{C)}=\text{-cosA}$ c) $ \tan (A+C)=-\tan B;\text{ cot(A}+\text{B)}=\text{-cotC}$
b) $ \text{sin}\frac{{\text{A}+\text{B}}}{\text{2}}=\cos \frac{C}{2}\text{; cos}\frac{{\text{B}+\text{C}}}{\text{2}}=\sin \frac{A}{2}$ d) $ \tan \frac{{A+C}}{2}=\cot \frac{B}{2};\text{ cot}\frac{{\text{A}+\text{B}}}{\text{2}}=\tan \frac{C}{2}$
5. Tìm giá trị lớn nhất của hàm số: $ y=\frac{{2+\cos x}}{{\sin x+\cos x-2}}$
6. Tìm giá trị nhỏ nhất và lớn nhất của hàm số trong khoảng $ -\pi <x<\pi $: $ y=\frac{{\cos x+2\sin x+3}}{{2\cos x-\sin x+4}}$.
7. Gọi a, b, c là các cạnh đối diện với các góc tương ứng của tam giác ABC.
a) Cho $ {{\sin }^{2}}B+{{\sin }^{2}}C=2{{\sin }^{2}}A$. Chứng minh $ \text{A}\le {{60}^{o}}$.
b) $ 2(a\cos A+b\cos B+c\cos C)=a+b+c\Rightarrow \Delta ABC$ đều.
c) Chứng minh: $ 0<\sin A+\sin B+\sin \text{C-sinA}\text{.sinB-sinB}\text{.sinC-sinC}\text{.sinA}<\text{1}$
Toán lớp 10 - Tags: hàm số, lượng giácPhương pháp giải toán hình học trên tọa độ Oxy lớp 10
Bài tập trắc nghiệm Số gần đúng và Sai số – Đại số 10
Bài tập trắc nghiệm Mệnh đề và suy luận toán học – Đại số 10
Ôn tập học kì 1 Toán 10: Đại số và Hình học
Đề cương ôn tập học kì 1 môn Toán lớp 10 THPT Chu Văn An năm 2017 – 2018
Bài tập chứng minh đẳng thức vectơ, phân tích vectơ
Cách chứng minh đường thẳng đi qua điểm cố định bằng vectơ
Từ khóa » Hàm Lượng Giác Toán 10
-
Các Công Thức Lượng Giác Toán 10 Đầy Đủ Nhất - Kiến Guru
-
Xem Bảng Công Thức Lượng Giác Đầy Đủ - Mathvn
-
Công Thức Lượng Giác đầy đủ Nhất Cho Lớp 9, Lớp 10, Lớp 11
-
Các Công Thức Lượng Giác Lớp 10 Cần Nhớ - Toán 10 - Hayhochoi
-
Các Công Thức Lượng Giác Lớp 10 Cơ Bản, Tổng Hợp đầy đủ - KhoiA.Vn
-
Giải Toán 10 Bài 3: Công Thức Lượng Giác
-
ĐẠO HÀM CỦA CÁC HÀM SỐ LƯỢNG GIÁC - TOÁN 10 - Hocmai
-
Cách Xác định Dấu Của Các Giá Trị Lượng Giác Lớp 10 - TopLoigiai
-
Cung Và Góc Lượng Giác - Môn Toán 10 - Thầy Giáo Nguyễn Công ...
-
Công Thức Lượng Giác - Phần 3 - Toán 10 - Thầy Nguyễn Công Chính
-
Bảng Công Thức Lượng Giác Dùng Cho Lớp 10 - 11 - 12
-
Bài Tập Công Thức Lượng Giác Lớp 10
-
[ TỔNG HỢP ] Các Công Thức Lượng Giác Toán 10 Từ A-Z - Fanhome