Chuyên đề Hệ Thức Lượng Trong Tam Giác
Có thể bạn quan tâm
- Trang Chủ
- Đăng ký
- Đăng nhập
- Upload
- Liên hệ

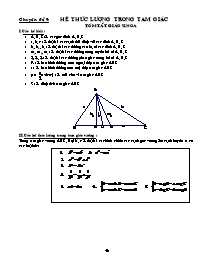
Chuyên đề 9: HỆ THỨC LƯỢNG TRONG TAM GIÁC
TÓM TẮT GIÁO KHOA
I. Các ký hiệu:
· A, B, C: là các góc đỉnh A, B, C
· a, b, c : là độ dài các cạnh đối diện với các đỉnh A, B, C
· ha, hb, hc : là độ dài các đường cao hạ từ các đỉnh A, B, C
· ma, mb, mc : là độ dài các đường trung tuyến kẻ từ A, B, C
· la, lb, lc : là độ dài các đường phân giác trong kẻ từ A, B, C
· R : là bán kính đường tròn ngoại tiếp tam giác ABC
· r : là bán kính đường tròn nội tiếp tam giác ABC
 ngochoa2017
ngochoa2017  6532
6532 1 Download Bạn đang xem tài liệu "Chuyên đề Hệ thức lượng trong tam giác", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trênChuyên đề 9: HỆ THỨC LƯỢNG TRONG TAM GIÁC TÓM TẮT GIÁO KHOA I. Các ký hiệu: A, B, C: là các góc đỉnh A, B, C a, b, c : là độ dài các cạnh đối diện với các đỉnh A, B, C ha, hb, hc : là độ dài các đường cao hạ từ các đỉnh A, B, C ma, mb, mc : là độ dài các đường trung tuyến kẻ từ A, B, C la, lb, lc : là độ dài các đường phân giác trong kẻ từ A, B, C R : là bán kính đường tròn ngoại tiếp tam giác ABC r : là bán kính đường tròn nội tiếp tam giác ABC p = (a+b+c) : là nữa chu vi tam giác ABC S : là diện tích tam giác ABC II. Các hệ thức lượng trong tam giác vuông : Trong tam giác vuông ABC . Gọi b', c' là độ dài các hình chiếu các cạnh góc vuông lên cạnh huyền ta có các hệ thức: II. Các hệ thức lượng trong tam giác thường 1. Định lý hàm số CÔSIN: Trong tam giác ABC ta luôn có : Ghi nhớ: Trong một tam giác, bình phương mỗi cạnh bằng tổng bình phương hai cạnh kia trừ đi hai lần tích hai cạnh ấy với côsin của góc xen giữa chúng. Hệ quả: Trong tam giác ABC ta luôn có : , , 2. Định lý hàm số SIN: Trong tam giác ABC ta có : Hệ quả: Với mọi tam giác ABC, ta có: Ghi nhớ: Trong một tam giác, tỷ số giữa một cạnh của tam giác và sin của góc đối diện với cạnh đó bằng đường kính đường tròn ngoại tiếp tam giác. 3. Định lý về đường trung tuyến: Trong tam giác ABC ta có : 4. Định lý về diện tích tam giác: Diện tích tam giác ABC được tính theo các công thức sau: 5. Định lý về đường phân giác: CÁC DẠNG TOÁN CƠ BẢN Dạng 1: CHỨNG MINH ĐẲNG THỨC LƯỢNG GIÁC TRONG TAM GIÁC Để chứng minh đẳng thức lượng giác A=B ta có thể thực hiện theo một trong các phương pháp sau Phương pháp 1: Biến đổi vế này thành vế kia Phương pháp 2: Xuất phát từ một một hệ thức đúng đã biết để suy ra đẳng thức cần chứng minh VÍ DỤ MINH HỌA: Ví dụ 1: Cho tam giác ABC. Chứng minh các đẳng thức sau: a) b) Ví dụ 2: Cho tam giác ABC. Chứng minh các đẳng thức sau: a) (ABC không vuông) b) Dạng 2: CHỨNG MINH BẤT ĐẲNG THỨC LƯỢNG GIÁC TRONG TAM GIÁC I. Bất đẳng thức trong tam giác : Nếu a, b, c là ba cạnh của một tam giác thì : a > 0, b > 0, c > 0 II. Các bất đẳng thức cơ bản : 1. Bất đẳng thức Cauchy: Cho hai số không âm a; b ta có : Dấu "=" xãy ra khi và chỉ khi a=b Tổng quát : Cho n số không âm a1,a2,...an ta có : Dấu "=" xãy ra khi và chỉ khi a1 = a2 =...= an 2 . Bất đẳng thức Bunhiacốpski : Cho bốn số thực a,b,x,y ta có : Dấu "=" xãy ra khi và chỉ khi ay = bx Tổng quát : Cho hai bộ số và ta có : Dấu "=" xãy ra khi và chỉ khi với quy ước rằng nếu mẫu bằng 0 thì tử cũng bằng 3) Bất đẳng thức cơ bản: a) Cho hai số dương x, y ta luôn có: Dấu "=" xãy ra khi và chỉ khi x = y b) Với mọi số thực x, y ta luôn có: Dấu "=" xãy ra khi và chỉ khi x = y III. Bất đẳng thức JENSEN : 1) Nếu hàm số y=f(x) có đạo hàm cấp hai f''(x) < 0 (f là hàm lồi) thì Với mọi ta có: Dấu "=" xãy ra khi và chỉ khi 2) Nếu hàm số y=f(x) có đạo hàm cấp hai f''(x) > 0 (f là hàm lõm) thì Với mọi ta có: Dấu "=" xãy ra khi và chỉ khi Để chứng minh đẳng thức lượng giác AB (>,) ta có thể thực hiện theo một trong các phương pháp sau: Phương pháp 1: Biến đổi bất đẳng thức cần chứng minh đến đến một bất đẳng thức hiển nhiên đúng Phương pháp 2: Sử dụng các bất đẳng thức cơ bản đã biết (Cô si, BCS,...) để suy ra bất đẳng thức cần chứng minh VÍ DỤ MINH HỌA: Ví dụ 1: Cho tam giác ABC. Chứng minh rằng: Ví dụ 2: Cho tam giác ABC. Chứng minh rằng: a) b) c) Ví dụ 3: Cho tam giác ABC. Chứng minh rằng: a) b) c) Dạng 3: NHẬN DẠNG TAM GIÁC KIỂU ĐỀ TOÁN 1: KIỂU ĐỀ TOÁN 2: "Điều kiện cho trước" có thể là: Đẳng thức lượng giác về góc Đẳng thức lượng giác + độ dài (cạnh, trung tuyến, phân giác,...) Đẳng thức độ dài Hệ đẳng thức 1) Nhận dạng tam giác vuông Phương pháp: Sử dụng các phép biến đổi tương đương hoặc hệ quả để biến đổi "Điều kiện cho trước" đến một đẳng thức mà từ đó ta dể dàng kết luận được tính chất của tam giác 2) Nhận dạng tam giác cân Phương pháp: Sử dụng các phép biến đổi tương đương hoặc hệ quả để biến đổi "Điều kiện cho trước" đến một đẳng thức mà từ đó ta dể dàng kết luận được tính chất của tam giác 3) Nhận dạng tam giác đều Ngoài phương pháp đã nêu trên ta có thể giải quyết bài toán theo cách sau Phương pháp sử dụng bất đẳng thức: Gồm 2 bước (áp dụng khi "Điều kiện cho trước" có dạng đẳng thức A = B Bước 1: CM bất đẳng thức hoặc (1) Bước 2: Lập luận để đẳng thức ở (1) xãy ra mà khi đẳng thức (1) xảy ra thì tam giác ABC đều VÍ DỤ MINH HỌA: Ví dụ 1: Tam giác ABC có . Chứng minh rằng ABC vuông Ví dụ 2: Chứng minh rằng nếu thỏa mãn điều kiện thì tam giác đó là tam giác vuông Ví dụ 3: Chứng minh rằng nếu tam giác ABC thoả mãn một trong các điều kiện sau là tam giác cân 1) 2) Ví dụ 4: Chứng minh rằng nếu tam giác ABC thoả mãn một trong các điều kiện sau là tam giác đều 1) 2) 3) 4) Ví dụ 5: Xác định dạng của tam giác ABC biết: 1) 2) 3) 4) Ví dụ 6: Hãy tính các góc của tam giác ABC nếu trong tam giác đó ta có : Ví dụ 7: Tính các góc của tam giác ABC biết rằng trong đó BC = a, AB = c, --------------------------------Hết---------------------------
1 Download Bạn đang xem tài liệu "Chuyên đề Hệ thức lượng trong tam giác", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trênChuyên đề 9: HỆ THỨC LƯỢNG TRONG TAM GIÁC TÓM TẮT GIÁO KHOA I. Các ký hiệu: A, B, C: là các góc đỉnh A, B, C a, b, c : là độ dài các cạnh đối diện với các đỉnh A, B, C ha, hb, hc : là độ dài các đường cao hạ từ các đỉnh A, B, C ma, mb, mc : là độ dài các đường trung tuyến kẻ từ A, B, C la, lb, lc : là độ dài các đường phân giác trong kẻ từ A, B, C R : là bán kính đường tròn ngoại tiếp tam giác ABC r : là bán kính đường tròn nội tiếp tam giác ABC p = (a+b+c) : là nữa chu vi tam giác ABC S : là diện tích tam giác ABC II. Các hệ thức lượng trong tam giác vuông : Trong tam giác vuông ABC . Gọi b', c' là độ dài các hình chiếu các cạnh góc vuông lên cạnh huyền ta có các hệ thức: II. Các hệ thức lượng trong tam giác thường 1. Định lý hàm số CÔSIN: Trong tam giác ABC ta luôn có : Ghi nhớ: Trong một tam giác, bình phương mỗi cạnh bằng tổng bình phương hai cạnh kia trừ đi hai lần tích hai cạnh ấy với côsin của góc xen giữa chúng. Hệ quả: Trong tam giác ABC ta luôn có : , , 2. Định lý hàm số SIN: Trong tam giác ABC ta có : Hệ quả: Với mọi tam giác ABC, ta có: Ghi nhớ: Trong một tam giác, tỷ số giữa một cạnh của tam giác và sin của góc đối diện với cạnh đó bằng đường kính đường tròn ngoại tiếp tam giác. 3. Định lý về đường trung tuyến: Trong tam giác ABC ta có : 4. Định lý về diện tích tam giác: Diện tích tam giác ABC được tính theo các công thức sau: 5. Định lý về đường phân giác: CÁC DẠNG TOÁN CƠ BẢN Dạng 1: CHỨNG MINH ĐẲNG THỨC LƯỢNG GIÁC TRONG TAM GIÁC Để chứng minh đẳng thức lượng giác A=B ta có thể thực hiện theo một trong các phương pháp sau Phương pháp 1: Biến đổi vế này thành vế kia Phương pháp 2: Xuất phát từ một một hệ thức đúng đã biết để suy ra đẳng thức cần chứng minh VÍ DỤ MINH HỌA: Ví dụ 1: Cho tam giác ABC. Chứng minh các đẳng thức sau: a) b) Ví dụ 2: Cho tam giác ABC. Chứng minh các đẳng thức sau: a) (ABC không vuông) b) Dạng 2: CHỨNG MINH BẤT ĐẲNG THỨC LƯỢNG GIÁC TRONG TAM GIÁC I. Bất đẳng thức trong tam giác : Nếu a, b, c là ba cạnh của một tam giác thì : a > 0, b > 0, c > 0 II. Các bất đẳng thức cơ bản : 1. Bất đẳng thức Cauchy: Cho hai số không âm a; b ta có : Dấu "=" xãy ra khi và chỉ khi a=b Tổng quát : Cho n số không âm a1,a2,...an ta có : Dấu "=" xãy ra khi và chỉ khi a1 = a2 =...= an 2 . Bất đẳng thức Bunhiacốpski : Cho bốn số thực a,b,x,y ta có : Dấu "=" xãy ra khi và chỉ khi ay = bx Tổng quát : Cho hai bộ số và ta có : Dấu "=" xãy ra khi và chỉ khi với quy ước rằng nếu mẫu bằng 0 thì tử cũng bằng 3) Bất đẳng thức cơ bản: a) Cho hai số dương x, y ta luôn có: Dấu "=" xãy ra khi và chỉ khi x = y b) Với mọi số thực x, y ta luôn có: Dấu "=" xãy ra khi và chỉ khi x = y III. Bất đẳng thức JENSEN : 1) Nếu hàm số y=f(x) có đạo hàm cấp hai f''(x) < 0 (f là hàm lồi) thì Với mọi ta có: Dấu "=" xãy ra khi và chỉ khi 2) Nếu hàm số y=f(x) có đạo hàm cấp hai f''(x) > 0 (f là hàm lõm) thì Với mọi ta có: Dấu "=" xãy ra khi và chỉ khi Để chứng minh đẳng thức lượng giác AB (>,) ta có thể thực hiện theo một trong các phương pháp sau: Phương pháp 1: Biến đổi bất đẳng thức cần chứng minh đến đến một bất đẳng thức hiển nhiên đúng Phương pháp 2: Sử dụng các bất đẳng thức cơ bản đã biết (Cô si, BCS,...) để suy ra bất đẳng thức cần chứng minh VÍ DỤ MINH HỌA: Ví dụ 1: Cho tam giác ABC. Chứng minh rằng: Ví dụ 2: Cho tam giác ABC. Chứng minh rằng: a) b) c) Ví dụ 3: Cho tam giác ABC. Chứng minh rằng: a) b) c) Dạng 3: NHẬN DẠNG TAM GIÁC KIỂU ĐỀ TOÁN 1: KIỂU ĐỀ TOÁN 2: "Điều kiện cho trước" có thể là: Đẳng thức lượng giác về góc Đẳng thức lượng giác + độ dài (cạnh, trung tuyến, phân giác,...) Đẳng thức độ dài Hệ đẳng thức 1) Nhận dạng tam giác vuông Phương pháp: Sử dụng các phép biến đổi tương đương hoặc hệ quả để biến đổi "Điều kiện cho trước" đến một đẳng thức mà từ đó ta dể dàng kết luận được tính chất của tam giác 2) Nhận dạng tam giác cân Phương pháp: Sử dụng các phép biến đổi tương đương hoặc hệ quả để biến đổi "Điều kiện cho trước" đến một đẳng thức mà từ đó ta dể dàng kết luận được tính chất của tam giác 3) Nhận dạng tam giác đều Ngoài phương pháp đã nêu trên ta có thể giải quyết bài toán theo cách sau Phương pháp sử dụng bất đẳng thức: Gồm 2 bước (áp dụng khi "Điều kiện cho trước" có dạng đẳng thức A = B Bước 1: CM bất đẳng thức hoặc (1) Bước 2: Lập luận để đẳng thức ở (1) xãy ra mà khi đẳng thức (1) xảy ra thì tam giác ABC đều VÍ DỤ MINH HỌA: Ví dụ 1: Tam giác ABC có . Chứng minh rằng ABC vuông Ví dụ 2: Chứng minh rằng nếu thỏa mãn điều kiện thì tam giác đó là tam giác vuông Ví dụ 3: Chứng minh rằng nếu tam giác ABC thoả mãn một trong các điều kiện sau là tam giác cân 1) 2) Ví dụ 4: Chứng minh rằng nếu tam giác ABC thoả mãn một trong các điều kiện sau là tam giác đều 1) 2) 3) 4) Ví dụ 5: Xác định dạng của tam giác ABC biết: 1) 2) 3) 4) Ví dụ 6: Hãy tính các góc của tam giác ABC nếu trong tam giác đó ta có : Ví dụ 7: Tính các góc của tam giác ABC biết rằng trong đó BC = a, AB = c, --------------------------------Hết--------------------------- Tài liệu đính kèm:
 He thuc luong.doc
He thuc luong.doc
 Giáo án Giải tích 12 bài 4: Đồ thị của hàm số và phép tịnh tiến hệ toạ độ
Giáo án Giải tích 12 bài 4: Đồ thị của hàm số và phép tịnh tiến hệ toạ độ Lượt xem: 1225
Lượt xem: 1225  Lượt tải: 0
Lượt tải: 0 Chuyên đề về Khảo sát hàm số
Chuyên đề về Khảo sát hàm số Lượt xem: 1545
Lượt xem: 1545  Lượt tải: 0
Lượt tải: 0 Giáo án Giải tích lớp 12 - Tiết 1: Sự đồng biến, nghịch biến của hàm số (tiết 1)
Giáo án Giải tích lớp 12 - Tiết 1: Sự đồng biến, nghịch biến của hàm số (tiết 1) Lượt xem: 1620
Lượt xem: 1620  Lượt tải: 0
Lượt tải: 0 Giáo án Giải tích 12 tiết 20, 21: Đường tiệm cận
Giáo án Giải tích 12 tiết 20, 21: Đường tiệm cận Lượt xem: 1430
Lượt xem: 1430  Lượt tải: 0
Lượt tải: 0 Một kiểu tư duy tìm lời giải cho một bài toán
Một kiểu tư duy tìm lời giải cho một bài toán Lượt xem: 1297
Lượt xem: 1297  Lượt tải: 0
Lượt tải: 0 Sáng tạo mới trong những bài toán cũ
Sáng tạo mới trong những bài toán cũ Lượt xem: 1043
Lượt xem: 1043  Lượt tải: 0
Lượt tải: 0 Đề và đáp án thi tốt nghiệp trung học phổ thông năm 2012 môn thi: Toán − Giáo dục thường xuyên
Đề và đáp án thi tốt nghiệp trung học phổ thông năm 2012 môn thi: Toán − Giáo dục thường xuyên Lượt xem: 1216
Lượt xem: 1216  Lượt tải: 0
Lượt tải: 0 Đề cương ôn tập Học kỳ 1 – Toán 12
Đề cương ôn tập Học kỳ 1 – Toán 12 Lượt xem: 1044
Lượt xem: 1044  Lượt tải: 0
Lượt tải: 0 Dạy phương trình lượng giác có tham số
Dạy phương trình lượng giác có tham số Lượt xem: 6042
Lượt xem: 6042  Lượt tải: 1
Lượt tải: 1 Đề thi chọn học sinh giỏi tỉnh Nghệ An lớp 12 năm học 2010 - 2011 môn thi: Toán 12 thpt - Bảng A
Đề thi chọn học sinh giỏi tỉnh Nghệ An lớp 12 năm học 2010 - 2011 môn thi: Toán 12 thpt - Bảng A Lượt xem: 1323
Lượt xem: 1323  Lượt tải: 0
Lượt tải: 0
Copyright © 2025 Lop12.net - Giáo án điện tử lớp 12, Sáng kiến kinh nghiệm hay, chia sẻ thủ thuật phần mềm


Từ khóa » Tính Chất Hệ Thức Lượng Trong Tam Giác
-
Lý Thuyết Các Hệ Thức Lượng Trong Tam Giác Và Giải Tam Giác
-
Hệ Thức Lượng Trong Tam Giác: Vuông, Cân, Thường Chính Xác 100%
-
Hệ Thức Lượng Trong Tam Giác Vuông, Cân, Thường Lớp 8, 9, Lớp ...
-
Các Hệ Thức Lượng Trong Tam Giác Thường, Và Tam Giác Vuông.
-
Hệ Thức Lượng Trong Tam Giác
-
Lý Thuyết Các Hệ Thức Lượng Trong Tam Giác Và Giải Tam ... - TopLoigiai
-
Tổng Quan Về Hệ Thức Lượng Trong Tam Giác Kèm 5 Ví Dụ Hay
-
Hệ Thức Lượng Giác Trong Tam Giác Vuông , Thường Có Công Thức Lớp ...
-
Công Thức Hệ Thức Lượng Trong Tam Giác Vuông, Tỉ Số Lượng Giác Của ...
-
Lý Thuyết: Hệ Thức Lượng Trong Tam Giác Vuông
-
Lý Thuyết Các Hệ Thức Lượng Trong Tam Giác Và Giải Tam Giác
-
Lý Thuyết Chương 1: Hệ Thức Lượng Trong Tam Giác Vuông đầy đủ Nhất
-
Hệ Thức Lượng Trong Tam Giác Vuông Lớp 8, Lớp 9 Từ Cơ Bản đến Nâng ...