Chuyên đề Khảo Sát Hàm Số - Tài Liệu ôn Tập Môn Toán Lớp 12

Download.vn Hướng dẫn sử dụng, mẹo vặt, thủ thuật phần mềm tài liệu và học tập Thông báo Mới

• Tất cả
  • Học tập
  • Tài liệu
  • Hướng dẫn
• • Học tập
  • Tài liệu
  • Hướng dẫn
  • Giáo án
  • Bài giảng điện tử
  • Đề thi
  • Tài liệu Giáo viên

Download.vn Học tập Lớp 12 Toán 12Chuyên đề khảo sát hàm số Tài liệu ôn tập môn Toán lớp 12Tải về Bình luận

• 4

Mua gói Pro để tải file trên Download.vn và trải nghiệm website không quảng cáo Tìm hiểu thêm Mua ngay

Chuyên đề khảo sát hàm số là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô giáo cùng các bạn học sinh lớp 12 cùng tham khảo.

Tài liệu gồm 177 trang hướng dẫn giải các dạng toán chuyên đề khảo sát hàm số, tài liệu do thầy Nguyễn Phú Khánh biên soạn. Nội dung tài liệu gồm 8 bài:

• Tính đơn điệu của hàm số;
• Cực trị hàm số;
• Tiệm cận của hàm số;
• Giá trị lớn nhất và nhỏ nhất của hàm số;
• Phép tịnh tiến và tâm đối xứng;
• Khảo sát sự biến thiên và vẽ đồ thị của hàm số;
• Giao điểm của hai đồ thị.
• Sự tiếp xúc của hai đường cong

Chuyên đề khảo sát hàm số

ŀNguyễn Phú Khánh – Đà Lạt Tài Liệu ôn thi Tú Tài Đại học theo cấu trúc BGD.5Chương 1ỨNG DỤNG CỦA ĐẠO HÀM ĐỂ KHẢO SÁTVÀ VẼ ĐỒ THỊ CỦA HÀM SỐBài 1: TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ1.1 TÓM TẮT LÝ THUYẾT1. Định nghĩa :Giả sửKlà một khoảng , một đoạn hoặc một nửa khoảng . Hàm sốfxác địnhtrênKđược gọi là•Đồng biến trênKnếu với mọi()()121212,,xxKxxfxfx∈<⇒<; •Nghịch biến trênKnếu với mọi()()121212,,xxKxxfxfx∈<⇒>. 2. Điều kiện cần để hàm số đơn điệu :Giả sửhàm sốfcó đạo hàm trên khoảngI•Nếu hàm sốfđồng biến trên khoảngIthì()'0fx≥với mọixI∈;•Nếu hàm sốfnghịch biến trên khoảngIthì()'0fx≤với mọixI∈.3. Điều kiện đủ để hàm số đơn điệu :Giả sửIlà một khoảng hoặc nửa khoảng hoặc một đoạn ,flà hàm số liên tụctrênIvà có đạo hàm tại mọi điểm trong củaI( tức là điểm thuộcInhưngkhông phải đầu mút củaI) .Khi đó :•Nếu()'0fx>với mọixI∈thì hàm sốfđồng biến trên khoảngI;•Nếu()'0fx<với mọixI∈thì hàm sốfnghịch biến trên khoảngI;•Nếu()'0fx=với mọixI∈thì hàm sốfkhông đổi trên khoảngI.Chú ý :•Nếu hàm sốfliên tục trên;abvà có đạo hàm()'0fx>trên khoảng();abthì hàm sốfđồng biến trên;ab.•Nếu hàm sốfliên tục trên;abvà có đạo hàm()'0fx<trên khoảng();abthì hàm sốfnghịch biến trên;ab.•Giả sử hàm sốfliên tục trên đoạn;ab.*Nếu hàm sốfđồng biến trên khoảng();abthì nó đồng biến trên đoạn;ab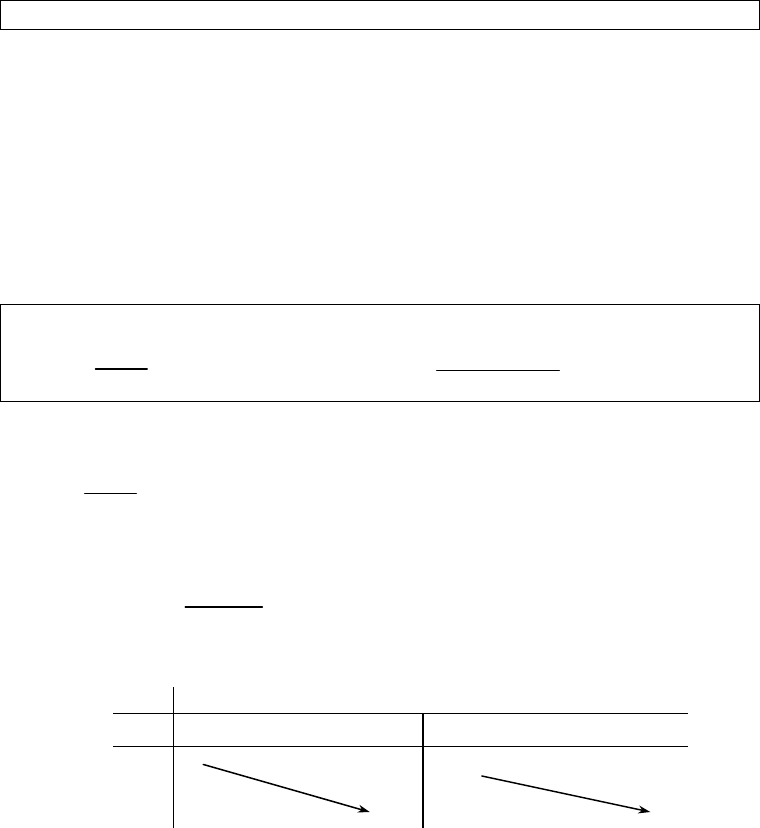.Nguyễn Phú Khánh – Đà Lạt Tài Liệu ôn thi Tú Tài Đại học theo cấu trúc BGD.6*Nếu hàm sốfnghịch biến trên khoảng();abthì nó nghịch biến trên đoạn;ab.*Nếu hàm sốfkhông đổi trên khoảng();abthì không đổi trên đoạn;ab.4. Định lý mở rộng Giả sử hàm sốfcó đạo hàm trên khoảngI.•Nếu'()0fx≥vớixI∀∈và'()0fx=chỉ tại một số hữu hạn điểm thuộcIthì hàm sốfđồng biến trên khoảngI;•Nếu'()0fx≤vớixI∀∈và'()0fx=chỉ tại một số hữu hạn điểm thuộcIthì hàm sốfnghịch biến trên khoảngI.1.2 DẠNG TOÁN THƯỜNG GẶPDạng 1 : Xét chiều biến thiên của hàm số .Xét chiều biến thiên của hàm số()yfx= ta thực hiện các bước sau: •Tìm tập xác địnhDcủa hàm số .•Tính đạo hàm()''yfx= . •Tìm các giá trị củaxthuộcDđể()'0fx=hoặc()'fxkhông xác định( ta gọi đó là điểm tới hạn hàm số ).•Xét dấu()''yfx= trên từng khoảng xthuộcD.•Dựa vào bảng xét dấu và điều kiện đủ suy ra khoảng đơn điệu của hàm số.Ví dụ 1: Xét chiều biến thiên của các hàm số sau: 21.1xyx+=−2212.2xxyx−+−=+Giải:21.1xyx+=−*Hàm số đã cho xác định trên khoảng()();11;−∞∪+∞.*Ta có:()23'0,11yxx-=<∀≠−*Bảng biến thiên:x−∞1+∞'y−−y1−∞+∞1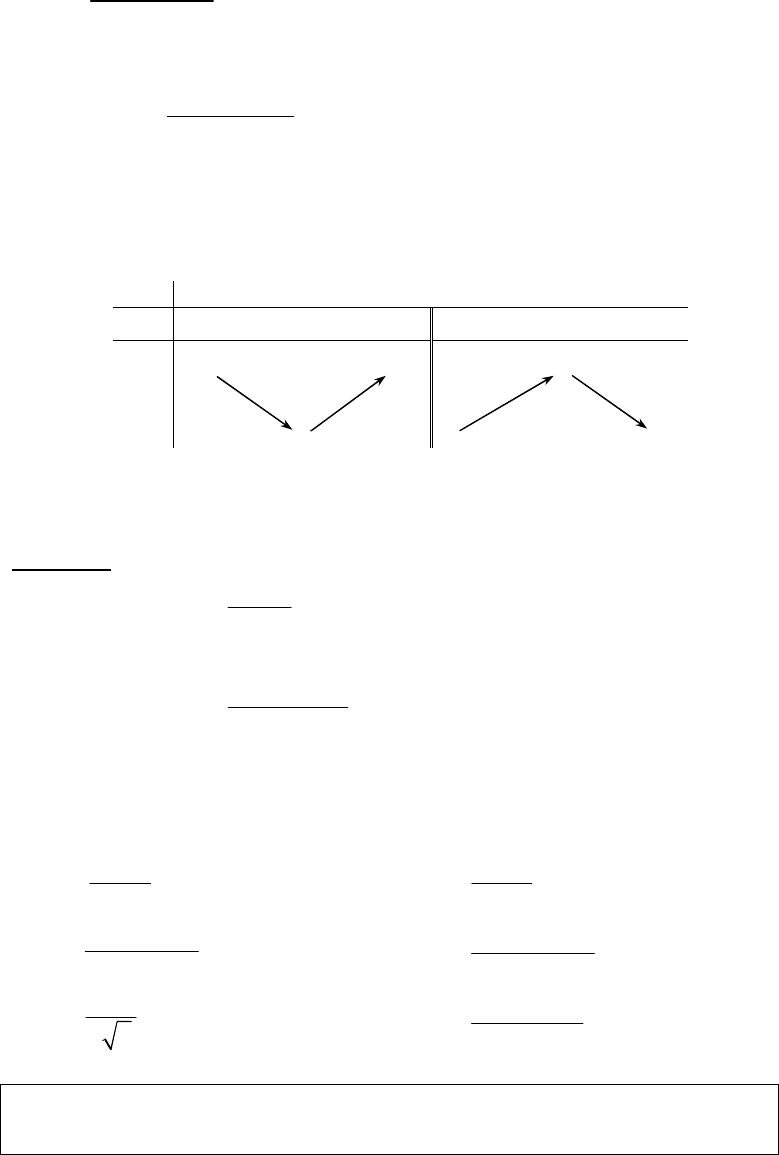Nguyễn Phú Khánh – Đà Lạt Tài Liệu ôn thi Tú Tài Đại học theo cấu trúc BGD.7Vậy hàm số đồng biến trên mỗi khoảng();1−∞và ()1;+∞.2212.2xxyx−+−=+*Hàm số đã cho xác định trên khoảng()();22;−∞−∪−+∞.*Ta có:()2245',22xxyxx−−+=∀≠−+5'01xyx=−=⇔=*Bảng biến thiên :x−∞5−2−1+∞'y−0++0−y+∞+∞−∞−∞Vậy, hàm số đồng biến trên các khoảng()5;2−−và()2;1−, nghịch biến trên các khoảng();5−∞−và()1;+∞.Nhận xét:* Đối với hàm số(.0)axbyaccxd+=≠+luôn đồng biến hoặc luôn nghịchbiến trên từng khoảng xác định của nó.* Đối với hàm số2''axbxcya xb++=+luôn có ít nhất hai khoảng đơn điệu.* Cả hai dạng hàm số trên không thể luôn đơn điệu trênℝ.Bài tập tương tự :Xét chiều biến thiên của các hàm số sau:211.1xyx−=+2432.2xxyx++=+13.3xyx+=234.1xyx=+22435.224xxyxx−+=−−22226.21xxyxx++=++Ví dụ 2: Xét chiều biến thiên của các hàm số sau: 321.32426yxxx=−−++ 422.681yxxx=−++Chia sẻ bởi: Trịnh Thị Thanh

Download

Liên kết tải về

Link Download chính thức:

Chuyên đề khảo sát hàm số 1,6 MB 21/03/2019 DownloadTìm thêm: Toán 12

Tài liệu tham khảo khác

Có thể bạn quan tâm

• 

  Văn mẫu lớp 9: Thuyết minh về cây chuối

  100.000+
• 

  Phân tích tác phẩm Mùa xuân chín (Dàn ý + 3 mẫu)

  100.000+
• 

  Văn mẫu lớp 9: Thuyết minh về cây dừa

  100.000+
• 

  Cảm nhận khổ 1 bài thơ Mùa xuân chín (Dàn ý + 2 mẫu)

  10.000+
• 

  Văn mẫu lớp 9: Đóng vai người lính kể lại bài thơ Ánh trăng của Nguyễn Duy

  100.000+
• 

  Văn mẫu lớp 6: Tóm tắt truyện cổ tích Sọ Dừa (16 mẫu)

  100.000+
• 

  Bài viết số 1 lớp 9 đề 2: Thuyết minh về một loài cây

  100.000+
• 

  Phân tích khổ 1 bài thơ Mùa xuân chín (Dàn ý + 2 Mẫu)

  10.000+
• 

  Văn mẫu lớp 9: Đóng vai người lính kể lại bài thơ Đồng Chí của Chính Hữu

  100.000+
• 

  Tập làm văn lớp 4: Kể một câu chuyện về lòng dũng cảm (8 mẫu)

  100.000+

Xem thêmSắp xếp theo Mặc địnhMới nhấtCũ nhấtXóa Đăng nhập để Gửi

Mới nhất trong tuần

• Vòng tròn lượng giác

  

• Các dạng bài tập cực trị của hàm số

  

• Tóm tắt lý thuyết và giải nhanh Toán 12

  

• Các dạng bài tập tính đơn điệu của hàm số

  

• 524 câu hỏi vận dụng cao trong các đề thi THPT Quốc gia

  

• Phương pháp tọa độ hóa hình không gian

  

• Bộ đề thi chọn học sinh giỏi môn Toán lớp 12

  

• Bộ đề thi khảo sát chất lượng đầu năm môn Toán lớp 12 năm 2023 - 2024

  

• Thể tích khối chóp: Công thức và bài tập

  

• Lý thuyết và bài tập trắc nghiệm số phức

  

Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm Mua Download Pro 79.000đ

Tài khoản

Gói thành viên

Giới thiệu

Điều khoản

Bảo mật

Liên hệ

Facebook

Twitter

DMCA

Giấy phép số 569/GP-BTTTT. Bộ Thông tin và Truyền thông cấp ngày 30/08/2021. Cơ quan chủ quản: CÔNG TY CỔ PHẦN MẠNG TRỰC TUYẾN META. Địa chỉ: 56 Duy Tân, Dịch Vọng Hậu, Cầu Giấy, Hà Nội. Điện thoại: 024 2242 6188. Email: info@meta.vn. Bản quyền © 2024 download.vn.