Chuyên đề Phương Trình Bậc Hai Chứa Tham Số Toán 9 (Có đáp án)

Chuyên đề Phương trình bậc hai chứa tham số Toán 9 (Có đáp án) Tài liệu đại số Toán 9 ôn thi vào 10 Bài trước Tải về Bài sau Lớp: Lớp 9 Môn: Toán Loại File: PDF Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Chuyên đề Phương trình bậc hai chứa tham số Toán 9

(Có đáp án)

Chuyên đề Phương trình bậc hai chứa tham số là dạng bài thường gặp trong chương trình Toán lớp 9 cũng như thi vào lớp 10. Để giúp các em học sinh nắm vững phần này, VnDoc gửi tới các bạn Chuyên đề Phương trình bậc hai chứa tham số. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hơn. 

Tài liệu Phương trình bậc hai chứa tham số được chia làm hai phần: Lý thuyết và bài tập vận dụng. Phần lý thuyết có các bài tập ví dụ để các bạn học sinh tham khảo. Phần bài tập được sưu tầm và chọn lọc để các bạn học sinh có thể áp dụng lý thuyết phía trên vận dụng làm bài. Qua đó sẽ giúp cho các bạn học sinh ôn tập và củng cố lại kiến thức về Phương trình bậc hai chứa tham số đồng thời nắm vững các kiến thức để chuẩn bị cho kì thi tuyển sinh vào lớp 10.

A. Công thức giải bài toán phương trình bậc hai chứa tham số 

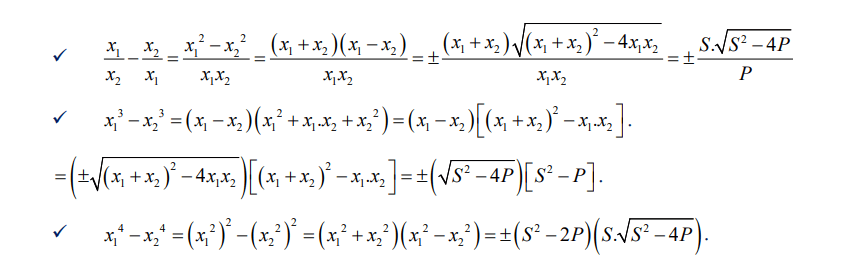
B. Các dạng bài tập về phương trình bậc hai chứa tham số có hướng dẫn 

Câu 1: Cho phương trình \(x^{2} - 2m + 1x + m^{2} + m - 1 = 0\) ( \(m\) là tham số).

a) Chứng minh rằng phương trình luôn có nghiệm vói mọi \(m\).

b) Gọi \(x_{1},x_{2}\) là hai nghiệm của phương trình. Tìm \(m\) sao cho \(A = \left( 2x_{1} - x_{2} \right)\left( 2x_{2} - x_{1} \right)\) đạt giá trị nhỏ nhất và tính giá trị nhỏ nhất đó.

Hướng dẫn giải 

Xét \(2m - 1 = 0 \Rightarrow m = \frac{1}{2}\) phương trình trở thành \(- x + 1 = 0 \Rightarrow x = 1 \notin ( - 1;0)\)

Xét \(2m - 1 \neq 0 \Rightarrow m \neq \frac{1}{2}\) khi đó ta có:

\(\Delta' = m^{2} - (2m - 1) = m^{2} -2m + 1 = (m - 1)^{2} \geq 0\) với mọi m

Suy ra phương trình có nghiệm với mọi \(m\).

Ta thấy nghiệm \(x = 1\) không thuộc khoảng \(( - 1;0)\)

Với \(m \neq \frac{1}{2}\) phương trình còn có nghiệm là \(x = \frac{m - m + 1}{2m - 1} = \frac{1}{2m - 1}\)

Phương trình có nghiệm trong khoáng \(( - 1;0)\) suy ra

\(- 1 \leq \frac{1}{2m - 1} \leq 0\Leftrightarrow \left\{ \begin{matrix}\dfrac{1}{2m - 1} + 1 > 0 \\2m - 1 < 0\end{matrix} \right.\)

\(\Leftrightarrow \left\{ \begin{matrix}\dfrac{2m}{2m - 1} > 0 \\2m - 1 < 0\end{matrix} \Rightarrow m < 0 \right.\)

Vậy phương trình đã cho có nghiệm trong khoảng \(( - 1;0)\) khi và chỉ khi \(m < 0\).

Câu 2: Cho phương trình \(x^{2} - 2mx + m^{2} - \frac{1}{2} = 0\) ( \(m\) là tham số).

a) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị \(m\).

b) Tìm \(m\) để hai nghiệm của phương trình có giá trị tuyệt đối bằng nhau.

c) Tìm \(m\) để hai nghiệm đó là số đo của 2 cạnh góc vuông của tam giác vuông có cạnh huyền bằng 3.

Hướng dẫn giải 

a) \(\ \Delta = (2m - 1)^{2} - 4 \cdot \left( m^{2} - 1 \right) = 5 - 4m\)

Phương trình có hai nghiệm phân biệt \(\Leftrightarrow m < \frac{5}{4}\)

b) Phương trình hai nghiệm \(\Leftrightarrow m < \frac{5}{4}\)

Áp dụng hệ thức Vi-ét, ta có: \(\left\{ \begin{matrix} x_{1} + x_{2} = 2m - 1 \\ x_{1}x_{2} = m^{2} - 1 \end{matrix} \right.\)

Theo đề bài:

\(\left( x_{1} - x_{2} \right)^{2} = x_{1} - 3x_{2}\)

\(\Leftrightarrow \left( x_{1} + x_{2} \right)^{2} - 4x_{1}x_{2} = x_{1} - 3x_{2}\)

\(\Leftrightarrow (2m - 1)^{2} - 4\left( m^{2} - 1 \right) = x_{1} - 3x_{2}\)

\(\Leftrightarrow x_{1} - 3x_{2} = 5 - 4m\)

Ta có hệ phương trình: \(\left\{\begin{matrix}x_{1} + x_{2} = 2m - 1 \\x_{1} - 3x_{2} = 5 - 4m\end{matrix} \Leftrightarrow \left\{ \begin{matrix}x_{1} = \dfrac{m + 1}{2} \\x_{2} = \dfrac{3(m - 1)}{2}\end{matrix} \right.\ \right.\)

\(\begin{matrix} \Rightarrow \frac{{m + 1}}{2}.\frac{{3\left( {m - 1} \right)}}{2} = {m^2} - 1 \hfill \\ \Rightarrow 3\left( {{m^2} - 1} \right) = 4\left( {{m^2} - 1} \right) \hfill \\ \Rightarrow {m^2} - 1 = 0 \Leftrightarrow \left[ \begin{gathered} m = 1 \hfill \\ m = - 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{matrix}\)

Kết hợp với điều kiện đề bài suy ra \(m = \pm 1\) là các giá trị cần tìm.

Câu 3: Cho phương trình \(x^{2} - 2x + m + 3 = 0\) ( \(m\) là tham số).

a) Tìm \(m\) để phương trình có nghiệm \(x = - 1\). Tính nghiệm còn lại.

b) Tìm \(m\) để hai nghiệm phân biệt \(x_{1},x_{2}\) thỏa mãn hệ thức \(x_{1}^{3} + x_{2}^{3} = 8\).

Hướng dẫn giải 

Ta có: \(\Delta = 5^{2} - 4.1 \cdot (3m - 1) = 29 - 12m\)

Để phương trình có hai nghiệm phân biệt \(\Rightarrow \Delta \geq 0 \Rightarrow m \leq \frac{29}{12}\)

Áp dụng hệ thức Vi-ét: \(\left\{ \begin{matrix} x_{1} + x_{2} = - 5 \\ x_{1}x_{2} = 3m - 1 \end{matrix} \right.\)

Ta có: \(x_{1}^{3} - x_{2}^{3} + 3x_{1}x_{2} = 75\)

\(\Leftrightarrow \left( x_{1} - x_{2} \right)\left( \left( x_{1} + x_{2} \right)^{2} - x_{1}x_{2} \right) + 3x_{1}x_{2} = 75\)

\(\Rightarrow \left( x_{1} - x_{2} \right)\left( 25 - x_{1}x_{2} \right) + 3x_{1}x_{2} = 75\)

\(\Leftrightarrow 25\left( x_{1} - x_{2} \right) - \left( x_{1} - x_{2} \right)x_{1}x_{2} + 3x_{1}x_{2} = 75\)

\(\Rightarrow x_{1} - x_{2} = 3\)

Kết hợp \(x_{1} + x_{2} = - 5\) suy ra \(x_{1} = - 1;x_{2} = - 4\)

Thay vào \(x_{1}x_{2} = 3m - 1\) suy ra \(m = \frac{5}{3}\)

Vậy \(m = \frac{5}{3}\) là giá trị cần tìm

Câu 4: Tìm các giá trị của tham số \(m\) để phương trình \(x^{2} + (2m - 1)x + m^{2} - 1 = 0\) có hai nghiệm phân biệt \(x_{1},x_{2}\) sao cho biểu thức \(P = x_{1}^{2} + x_{2}^{2}\) đạt giá trị nhỏ nhất.

Hướng dẫn giải 

a) Với \(m = 1\) phương trình đã cho trở thành \(x^{2} - 10x + 9 = 0\)

Ta có: \(a + b + c = 0\) nên phương trình có hai nghiệm phân biệt là \(\left\lbrack \begin{matrix} x_{1} = 1 \\ x_{2} = 9 \end{matrix} \right.\)

b) \(\ \Delta' = ( - 5m)^{2} - 1.9m = 25m^{2} - 9m\)

Điều kiện phương trình đã cho có hai nghiệm phân biệt là