Chuyên đề: Tam Thức Bậc Hai - Toán Lớp 10 - Abcdonline

Trang chủ » Dấu Tam Thức Bậc 2 Lớp 10 » Chuyên đề: Tam Thức Bậc Hai - Toán Lớp 10 - Abcdonline

Có thể bạn quan tâm

Chuyên đề: Tam thức bậc hai – Toán lớp 10

Cách xét dấu của tam thức bậc hai, các dạng bài tập về tam thức bậc hai trong chương trình Đại số 10 – Toán lớp 10 .

Trong bài viết này chúng ta ôn lại lý thuyết định lý về dấu của tam thức bậc hai: định lý thuận, định lý đảo, cách so sánh nghiệm của tam thức bậc hai với một số, hai số, cách chứng minh phương trình bậc hai có nghiệm, biện luận nghiệm của PT bậc hai.

I. Lí thuyết về tam thức bậc hai

f(x) = ax2 + bx + c (a ≠ 0)

Kí hiệu: x1, x2 là nghiệm của f(x) = 0

1. Định lí thuận về dấu của tam thức bậc hai

(trong trái, ngoài cùng)

+ Δ < 0 → af(x) > 0 với \displaystyle \forall x\in R

+ Δ = 0 → af(x) > 0 với \displaystyle \forall x\ne -\frac{b}{{2a}} hoặc af(x) ≥ 0 với \displaystyle \forall x\in R

+ Δ > 0 → \displaystyle \left\{ \begin{array}{l}af(x)>0\Leftrightarrow \left[ \begin{array}{l}x<{{x}_{1}}\\x>{{x}_{2}}\end{array} \right.\\af(x)<0\Leftrightarrow {{x}_{1}}<x<{{x}_{2}}\end{array} \right.

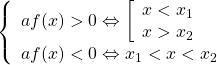
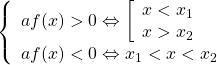
2. Định lí đảo về dấu của tam thức bậc hai

a. Nội dung: Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0). Nếu có số α thoả mãn af(α) < 0 thì f(x) có hai nghiệm phân biệt x1, x2 và x1 < α < x2. b. Hệ quả: + \displaystyle af(\alpha )<0\Leftrightarrow \left\{ \begin{array}{l}\Delta >0\\{{x}_{1}}<\alpha <{{x}_{2}}\end{array} \right.

+ \displaystyle af(\alpha )=0\Leftrightarrow \alpha là nghiệm của f(x)

+ \displaystyle \left\{ \begin{array}{l}af(\alpha )>0\\\Delta >0\end{array} \right.\Rightarrow \alpha \notin [{{x}_{1}};{{x}_{2}}]\text{ }. Xảy ra 2 trường hợp:

. \displaystyle \alpha <{{\text{x}}_{\text{1}}}<{{x}_{2}} khi \displaystyle \frac{S}{2}>\alpha

. \displaystyle {{\text{x}}_{\text{1}}}<{{x}_{2}}<\alpha khi \displaystyle \frac{S}{2}<\alpha

II. Các dạng bài tập

1. So sánh nghiệm của tam thức với một số cho trước

+ \displaystyle {{x}_{1}}<\alpha <{{x}_{2}}\Leftrightarrow af(\alpha )<0

+ \displaystyle \alpha <{{x}_{1}}<{{x}_{2}}\Leftrightarrow \left\{ \begin{array}{l}\Delta >0\\af(\alpha )>0\\\frac{S}{2}-\alpha >0\end{array} \right.

+ \displaystyle {{x}_{1}}<{{x}_{2}}<\alpha \Leftrightarrow \left\{ \begin{array}{l}\Delta >0\\af(\alpha )>0\\\frac{S}{2}-\alpha <0\end{array} \right.

+ \displaystyle \alpha \notin [{{x}_{1}};{{x}_{2}}]\Leftrightarrow \left\{ \begin{array}{l}\Delta >0\\af(\alpha )>0\end{array} \right.

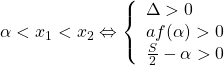
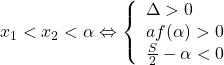
2. So sánh nghiệm của tam thức với hai số cho trước α < β

+ \displaystyle {{x}_{1}}<\alpha <\beta <{{x}_{2}}\Leftrightarrow \left\{ \begin{array}{l}af(\alpha )<0\\af(\beta )<0\end{array} \right.

+ \displaystyle {{x}_{1}}<\alpha <{{x}_{2}}<\beta \Leftrightarrow \left\{ \begin{array}{l}af(\alpha )<0\\af(\beta )>0\end{array} \right.

+ \displaystyle \alpha <{{x}_{1}}<\beta <{{x}_{2}}\Leftrightarrow \left\{ \begin{array}{l}af(\alpha )>0\\af(\beta )<0\end{array} \right. + Phương trình có hai nghiệm phân biệt và chỉ có một nghiệm thuộc khoảng (α;β) khi f(α).f(β) < 0

+ Phương trình có hai nghiệm phân biệt và \displaystyle \alpha <{{x}_{1}}<{{x}_{2}}<\beta \Leftrightarrow \left\{ \begin{array}{l}\Delta >0\\af(\alpha )>0\\af(\beta )>0\\\frac{S}{2}-\alpha >0\\\frac{S}{2}-\beta <0\end{array} \right.

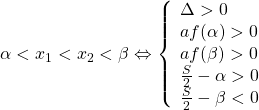
3. Tìm điều kiện để tam thức bậc hai không đổi dấu trên R, trên một miền cho trước

+ \displaystyle f(x)>0,\forall x\in R\Leftrightarrow \left\{ \begin{array}{l}a>0\\\Delta <0\end{array} \right.

+ \displaystyle f(x)\ge 0,\forall x\in R\Leftrightarrow \left\{ \begin{array}{l}a>0\\\Delta \le 0\end{array} \right.

+ \displaystyle f(x)<0,\forall x\in R\Leftrightarrow \left\{ \begin{array}{l}a<0\\\Delta <0\end{array} \right.

+ \displaystyle f(x)\le 0,\forall x\in R\Leftrightarrow \left\{ \begin{array}{l}a<0\\\Delta \le 0\end{array} \right.

4. Chứng minh phương trình bậc hai có nghiệm

+ Nếu có α sao cho af(α) < 0 thì phương trình có hai nghiệm phân biệt.

+ Nếu có hai số α, β sao cho f(α).f(β) < 0 thì phương trình f(x) = 0 có nghiệm.

+ Nếu có hai số α, β sao cho f(α).f(β) < 0 và a ≠ 0 thì phương trình f(x) = 0 có hai nghiệm phân biệt.

5. Giải và biện luận phương trình, bất phương trình bậc hai

Lập bảng xét dấu

maΔf(α)S/2 – αf(β)S/2 – βKết luận

III. Bài tập về dấu của tam thức bậc 2

Bài 1: So sánh 1 với nghiệm của phương trình: 2x2 – 18x + 17 = 0 [TD10BD70]

Bài 2: So sánh – 2 với nghiệm của phương trình: f(x) = (m2 + 1)x2 – 5(m2 + 1)x – m2 + m – 1 = 0 [TD11BD70]

Bài 3: Tìm m để các phương trình sau có hai nghiệm:

a. mx2 + (m – 1)x + 3 – 4m = 0 và thoả mãn x1 < 2 < x2

b. (m + 1)x2 – (m – 3)x + m + 1 = 0 và thoả mãn -1 < x1 ≤ x2

c. (m + 1)x2 + mx + 3 = 0 và thoả mãn x1 < – 2 < 1 < x2

d. x2 – 2mx + m = 0 và thoả mãn x1, x2 \displaystyle \in(-1;3)

e. x2 – 2x – 3m = 0 và thoả mãn \displaystyle \frac{m}{2}\le {{x}_{1}}<1<{{x}_{2}}

Bài 4: Tìm m sao cho:

f(x) = 2x2 – 2(m + 1)x + 2m + 1 > 0 \displaystyle \forall x\in R

f(x) = (m – 1)x2 – (m – 1)x + 1 – 2m ≤ 0 \displaystyle \forall x\in R.

Bài 5: Tìm m để bất phương trình f(x) = mx2 – (2m – 1)x + m + 1 < 0 vô nghiệm.

Bài 6: Định m để: \displaystyle \left| {\frac{{{{x}^{2}}+x+4}}{{{{x}^{2}}-mx+4}}} \right|\le 2 với \displaystyle \forall x\in R.

Bài 7: Tìm m để phương trình sau có nghiệm:

a. (x2 + 2x)2 – 4m(x2 + 2x) + 3m + 1 = 0.

b. x4 + mx3 + 2mx2 + mx + 1 = 0.

Bài 8: Tìm m để phương trình: (m + 1)x2 – 3mx + 4m = 0 có duy nhất một nghiệm lớn hơn 1.

Bài 9: Tìm m sao cho: f(x) = (m + 2)x2 – 2(m + 3)x – m + 3 > 0 với \displaystyle \forall x\in (-\infty ;1).

Bài 10: CMR phương trình f(x) = m(x2 – 9) + x(x – 5) = 0 luôn có nghiệm.

Bài 11: Giải và biện luận phương trình: \displaystyle \frac{1}{{\sqrt{{{{x}^{2}}+2mx}}}}=\frac{1}{{\sqrt{{8x-6m-3}}}}(1).

Bài 12: Với giá trị nào của m thì: \displaystyle 1<\frac{{3{{x}^{2}}-mx+5}}{{2{{x}^{2}}-x+1}}\le 6;\forall x\in R.

Bài 13: Tìm m để \displaystyle {{x}^{2}}-2mx-m+2\ge 0;\forall x\notin (-1;2].

Đại số 10 - Tags: tam thức, tam thức bậc hai, toán 10

  • Cách so sánh nghiệm của tam thức bậc 2 với các số α, β

  • Tóm tắt kiến thức Toán lớp 10: Đại số 10 và Hình học 10

Từ khóa » Dấu Tam Thức Bậc 2 Lớp 10