Chuyên đề Vectơ Trong Không Gian, Quan Hệ Vuông Góc
Có thể bạn quan tâm
- 1
Mua gói Pro để tải file trên Download.vn và trải nghiệm website không quảng cáo
Tìm hiểu thêm » Mua Pro 79.000đ Hỗ trợ qua ZaloNhằm mang đến cho học sinh lớp 11 có thêm nhiều tài liệu học chương trình Hình học 11 chương 3, Download.vn xin giới thiệu tài liệu Chuyên đề vectơ trong không gian, quan hệ vuông góc.
Tài liệu gồm 99 trang với đầy đủ lý thuyết, dạng toán và bài tập chủ đề vectơ trong không gian, quan hệ vuông góc, sẽ giúp các em dễ dàng tiếp cận và học tốt hơn hình học không gian. Sau đây là nội dung chi tiết mời các em cùng tham khảo và tải tài liệu tại đây.
Chuyên đề vectơ trong không gian, quan hệ vuông góc
 GV. TRGV. TRGV. TRGV. TRẦẦẦẦN QUN QUN QUN QUỐỐỐỐC NGHC NGHC NGHC NGHĨAĨAĨAĨA 1111 VÉCTƠ TRONG KHÔNG GIAN QUAN HỆ VUÔNG GÓC Vấn đề 1. VÉCTƠ TRONG KHÔNG GIAN I.Véctơtrongkhônggian①①①① Véctơ, giá và độ dài của véctơ. Véctơ trong không gian là một đoạn thẳng có hướng. Kí hiệuAB chỉ véctơ có điểm đầu A, điểm cuối B. Véctơ còn được kí hiệu a, b, c, … Giá của véctơ là đường thẳng đi qua điểm đầu và điểm cuối của véctơ đó. Hai véctơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau. Ngược lại, hai véctơ có giá cắt nhau được gọi là hai véctơ không cùng phương. Hai véctơ cùng phương thì có thể cùng hướng hoặc ngược hướng. Độ dài của véctơ là độ dài của đoạn thẳng có hai đầu mút là điểm đầu và điểm cuối của véctơ. Véctơ có độ dài bằng 1 gọi là véctơ đơn vị. Kí hiệu độ dài véctơ AB là AB Như vậy: ABABBA==. ②②②② Hai véctơ bằng nhau, đối nhau. Cho hai véctơ a, b(≠ 0) Hai véctơ a và b được gọi là bằng nhau nếu chúng có cùng hướng và cùng độ dài.Kí hiệu ab= và ||||ababab=⇔=cuønghöôùng Hai véctơ a và được gọi là đối nhau nếu chúng ngược hướng và cùng độ dài.Kí hiệu ab=− và ||||ababab=⇔=cuønghöôùng ③③③③ Véctơ – không. Véctơ – không là véctơ có điểm đầu và điểm cuối trùng nhau. Kí hiệu: 0, ...0AABBCC====. Véctơ – không có phương, hướng tùy ý, có độ dài bằng không.Véctơ – không cùng phương, cùng hướng với mọi véctơ. II.Phépcộngvàphéptrừvéctơ①①①① Định nghĩa 1. Cho a và b. Trong không gian lấy một điểm A tùy ý, dựng ABa=, BCb=. Véctơ AC được gọi là tổng của hai véctơ a và bvà được kí hiệu ACABBCab=+=+. ()abab−=+− ②②②② Tính chất 1. Tính chất giao hoán: abba+=+ Tính chất kết hợp: ()()abcabc++=++ Cộng với 0: 00aaa+=+= Cộng với véctơ đối: ()0aaaa+−= −+= abABCabab+8 Chủđề
GV. TRGV. TRGV. TRGV. TRẦẦẦẦN QUN QUN QUN QUỐỐỐỐC NGHC NGHC NGHC NGHĨAĨAĨAĨA 1111 VÉCTƠ TRONG KHÔNG GIAN QUAN HỆ VUÔNG GÓC Vấn đề 1. VÉCTƠ TRONG KHÔNG GIAN I.Véctơtrongkhônggian①①①① Véctơ, giá và độ dài của véctơ. Véctơ trong không gian là một đoạn thẳng có hướng. Kí hiệuAB chỉ véctơ có điểm đầu A, điểm cuối B. Véctơ còn được kí hiệu a, b, c, … Giá của véctơ là đường thẳng đi qua điểm đầu và điểm cuối của véctơ đó. Hai véctơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau. Ngược lại, hai véctơ có giá cắt nhau được gọi là hai véctơ không cùng phương. Hai véctơ cùng phương thì có thể cùng hướng hoặc ngược hướng. Độ dài của véctơ là độ dài của đoạn thẳng có hai đầu mút là điểm đầu và điểm cuối của véctơ. Véctơ có độ dài bằng 1 gọi là véctơ đơn vị. Kí hiệu độ dài véctơ AB là AB Như vậy: ABABBA==. ②②②② Hai véctơ bằng nhau, đối nhau. Cho hai véctơ a, b(≠ 0) Hai véctơ a và b được gọi là bằng nhau nếu chúng có cùng hướng và cùng độ dài.Kí hiệu ab= và ||||ababab=⇔=cuønghöôùng Hai véctơ a và được gọi là đối nhau nếu chúng ngược hướng và cùng độ dài.Kí hiệu ab=− và ||||ababab=⇔=cuønghöôùng ③③③③ Véctơ – không. Véctơ – không là véctơ có điểm đầu và điểm cuối trùng nhau. Kí hiệu: 0, ...0AABBCC====. Véctơ – không có phương, hướng tùy ý, có độ dài bằng không.Véctơ – không cùng phương, cùng hướng với mọi véctơ. II.Phépcộngvàphéptrừvéctơ①①①① Định nghĩa 1. Cho a và b. Trong không gian lấy một điểm A tùy ý, dựng ABa=, BCb=. Véctơ AC được gọi là tổng của hai véctơ a và bvà được kí hiệu ACABBCab=+=+. ()abab−=+− ②②②② Tính chất 1. Tính chất giao hoán: abba+=+ Tính chất kết hợp: ()()abcabc++=++ Cộng với 0: 00aaa+=+= Cộng với véctơ đối: ()0aaaa+−= −+= abABCabab+8 Chủđề 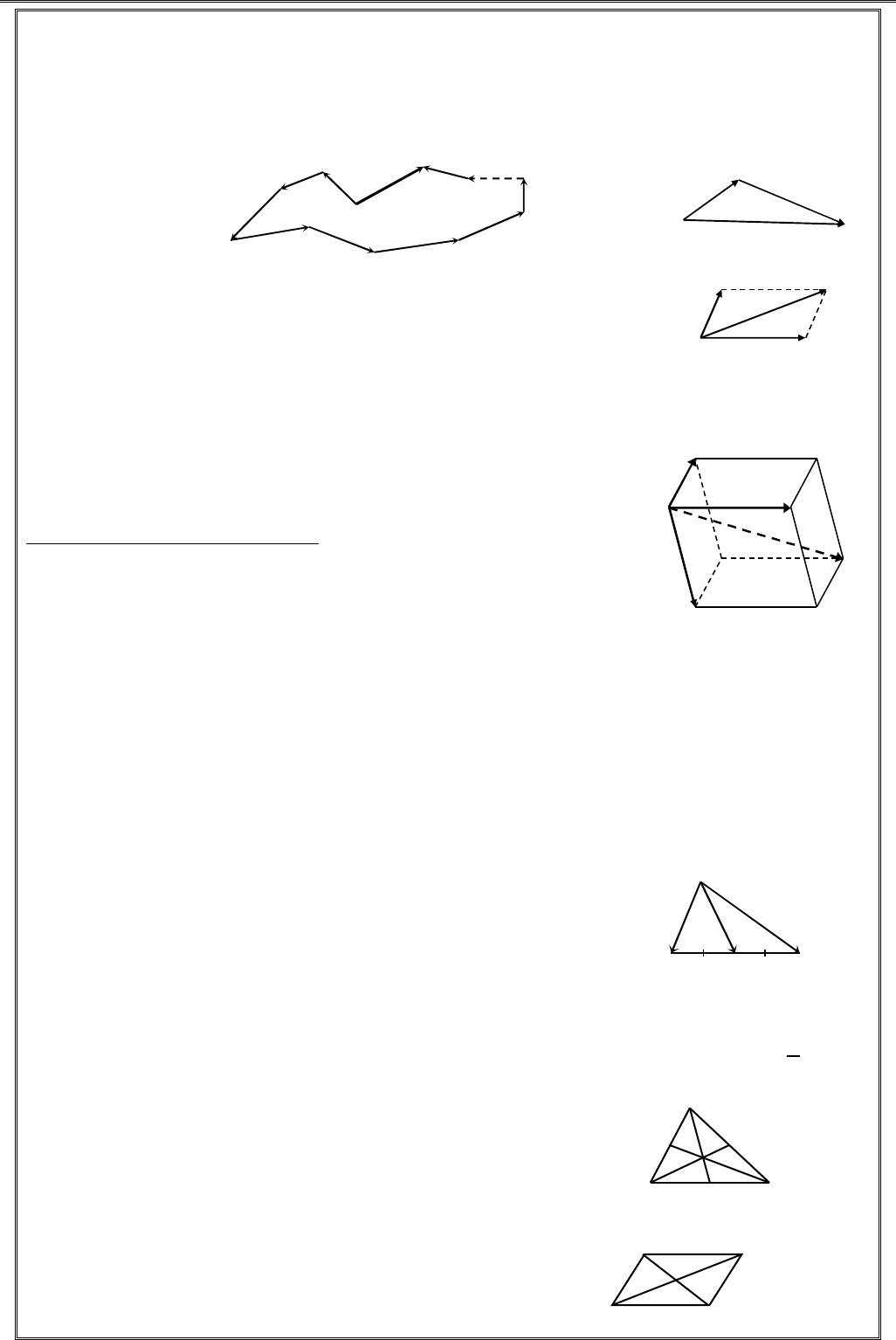 TÀI LITÀI LITÀI LITÀI LIỆỆỆỆU HU HU HU HỌỌỌỌC TC TC TC TẬẬẬẬP TOÁN 11P TOÁN 11P TOÁN 11P TOÁN 11 –––– HK2HK2HK2HK2 2222 ③③③③ Các qui tắc. Qui tắc ba điểm: Với ba điểm A, B, C bất kì ta có: ACABBC=+ Mở rộng: Qui tắc đa giác khép kínCho n điểm bất kì 123–1, , , , , nnAAAAA…. Ta có: 122311nnnAAAAAAAA−+++=… Qui tắc trừ (ba điểm cho phép trừ): Với ba điểm A, B, C bất kì ta có: ACBCBA=− Qui tắc hình bình hành: Với hình bình hành ABCD ta có: ACABAD=+ và DBABAD=− Qui tắc hình hộp. Cho hình hộp .ABCD ABCD′′′′ với AB, AD, AA′ là ba cạnh có chung đỉnh A và AC′ là đường chéo, ta có: ACABADAA′′=++ III.Phépnhânmộtsốvớimộtvéctơ①①①① Định nghĩa 2. Cho 0k≠ và véctơ 0a≠. Tích .k a là một véctơ: - Cùng hướng với a nếu 0k> - Ngược hướng với a nếu 0k< ②②②② Tính chất 2. Với a, b bất kì; ,mnR∈, ta có: ()mabmamb+=+ ()mnamana+=+ ()()mnamna= 1.aa=, ()1.aa−=− 0.0a=; .00k= ③③③③ Điều kiện để hai véctơ cùng phương. Cho hai véctơ a và b (0≠),0k≠: a cùng phương b ⇔ akb= Hệ quả: điều kiện để ba điểm A, B, C thẳng hàng là ABkAC= ④④④④ Một số tính chất. Tính chất trung điểm Cho đoạn thẳng AB có I là trung điểm, ta có: 0IAIB+=; IAIB=−; 12AIIBAB== 2MAMBMI+= (M bất kì) Tính chất trọng tâm. Cho ABC∆, G là trọng tâm, ta có: 0GAGBGC++= 3MAMBMCMG++= (M bất kì) Tính chất hình bình hành. Cho hình bình hành ABCD tâm O, ta có: 0OAOBOCOD+++= 4MAMBMCMDMO+++= 1A2A3A4A5A7A8A9A10An-1AnAABCABCDABCDA'B'C'D'MAIBABCGABCDO
TÀI LITÀI LITÀI LITÀI LIỆỆỆỆU HU HU HU HỌỌỌỌC TC TC TC TẬẬẬẬP TOÁN 11P TOÁN 11P TOÁN 11P TOÁN 11 –––– HK2HK2HK2HK2 2222 ③③③③ Các qui tắc. Qui tắc ba điểm: Với ba điểm A, B, C bất kì ta có: ACABBC=+ Mở rộng: Qui tắc đa giác khép kínCho n điểm bất kì 123–1, , , , , nnAAAAA…. Ta có: 122311nnnAAAAAAAA−+++=… Qui tắc trừ (ba điểm cho phép trừ): Với ba điểm A, B, C bất kì ta có: ACBCBA=− Qui tắc hình bình hành: Với hình bình hành ABCD ta có: ACABAD=+ và DBABAD=− Qui tắc hình hộp. Cho hình hộp .ABCD ABCD′′′′ với AB, AD, AA′ là ba cạnh có chung đỉnh A và AC′ là đường chéo, ta có: ACABADAA′′=++ III.Phépnhânmộtsốvớimộtvéctơ①①①① Định nghĩa 2. Cho 0k≠ và véctơ 0a≠. Tích .k a là một véctơ: - Cùng hướng với a nếu 0k> - Ngược hướng với a nếu 0k< ②②②② Tính chất 2. Với a, b bất kì; ,mnR∈, ta có: ()mabmamb+=+ ()mnamana+=+ ()()mnamna= 1.aa=, ()1.aa−=− 0.0a=; .00k= ③③③③ Điều kiện để hai véctơ cùng phương. Cho hai véctơ a và b (0≠),0k≠: a cùng phương b ⇔ akb= Hệ quả: điều kiện để ba điểm A, B, C thẳng hàng là ABkAC= ④④④④ Một số tính chất. Tính chất trung điểm Cho đoạn thẳng AB có I là trung điểm, ta có: 0IAIB+=; IAIB=−; 12AIIBAB== 2MAMBMI+= (M bất kì) Tính chất trọng tâm. Cho ABC∆, G là trọng tâm, ta có: 0GAGBGC++= 3MAMBMCMG++= (M bất kì) Tính chất hình bình hành. Cho hình bình hành ABCD tâm O, ta có: 0OAOBOCOD+++= 4MAMBMCMDMO+++= 1A2A3A4A5A7A8A9A10An-1AnAABCABCDABCDA'B'C'D'MAIBABCGABCDO 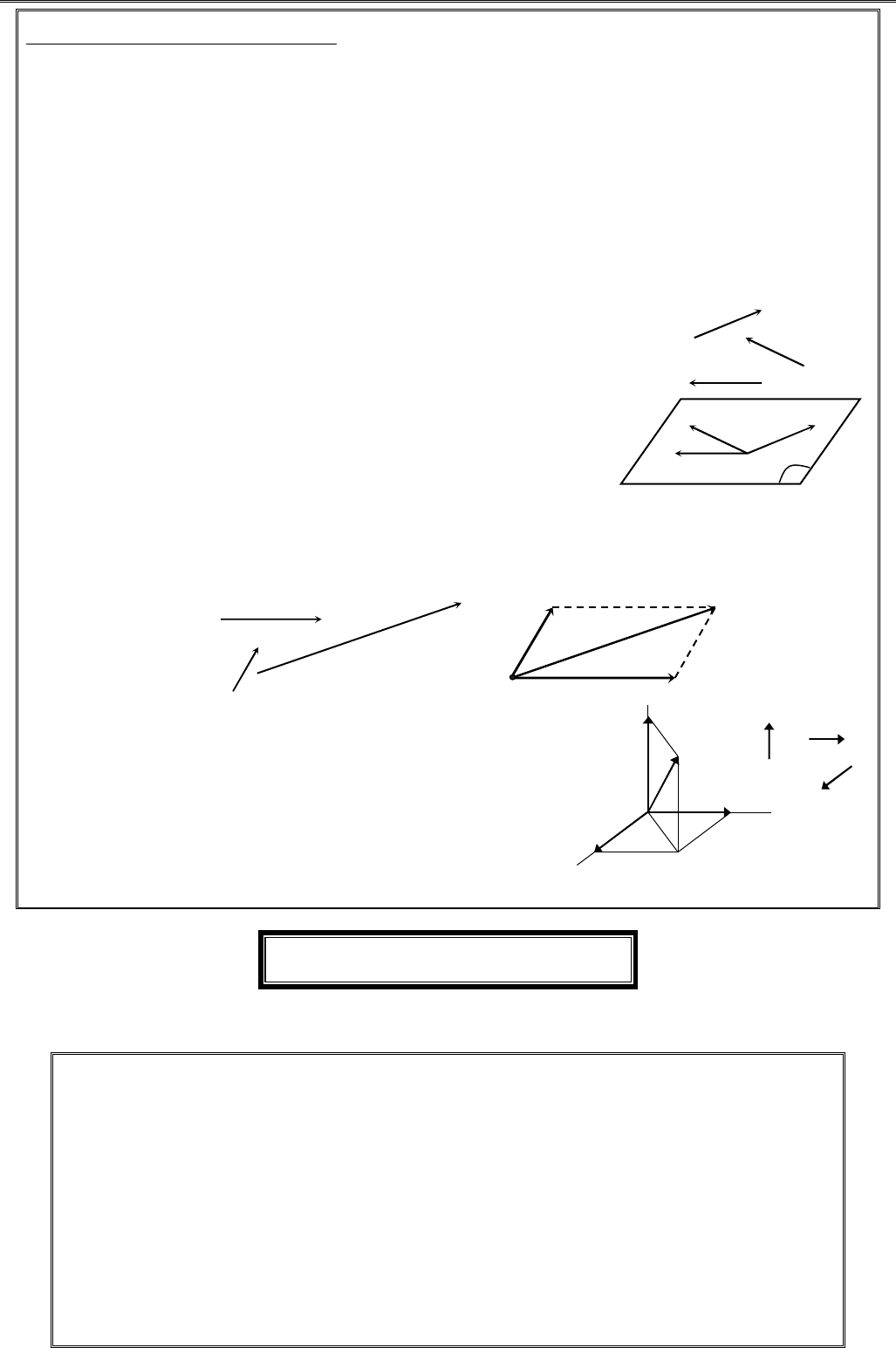 GV. TRGV. TRGV. TRGV. TRẦẦẦẦN QUN QUN QUN QUỐỐỐỐC NGHC NGHC NGHC NGHĨAĨAĨAĨA 3333 IV.Điềukiệnđểbavéctơđồngphẳng①①①① Khái niện về sự đồng phẳng của ba véctơ trong không gian. Cho ba véctơ a, b, c (≠0) trong không gian. Từ một điểm O bất kì ta dựng OAa=, OBb=, OCc=. Khi đó xảy ra hai trường hợp: Các đường thẳng OA, OB, OC không cùng nằm trong một mặt phẳng thì ta nói ba véctơ a,b,c không đồng phẳng. Các đường thẳng OA, OB, OC cùng nằm trong một mặt phẳng thì ta nói ba véctơ a, b,c đồng phẳng. ②②②② Định nghĩa 3. Ba véctơ gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng. Trên hình bên, giá của các véctơ a, b, c cùng song song với mặt phẳng (α) nên ba véctơ a, b, c đồng phẳng. ③③③③ Điều kiện để ba véctơđồng phẳng Định lí 1.Cho ba véctơ a, b, c trong đó a và b không cùng phương. Điều kiện cần và đủ để ba véctơ a, b, c đồng phẳng là có duy nhất các sốm, n sao cho cmanb=+. ④④④④ Phân tích một véctơ theo ba véctơ không đồng phẳng Định lí 2. Nếu ba véctơ a, b, c không đồng phẳng thì với mỗi véctơ d, ta tìm được duy nhất các số m, n, p sao cho dmanbpc=++. Dạng1.TínhtoánvéctơA. PHƯƠNG PHÁP GIẢI ①①①①Quy tắc ba điểm: ABACCB=+ (quy tắc cộng) ABCBCA=− (quy tắc trừ) ②②②②Quy tắc hình bình hành: Với hình bình hành ABCD ta luôn có: ACABAD=+ ③③③③Quy tắc hình hộp: Cho hình hộp .ABCD ABCD′′′′, ta được: ACABADAA′′=++ ④④④④Quy tắc trung điểm: Cho I là trung điểm AB, M là điển bất kỳ: 0IAIB+= và 2MAMBMI+= ⑤⑤⑤⑤Tính chất trọng tâm của tam giác: G là trọng tâm ABC∆, M∀ ta có: 0GAGBGC++= và 3MAMBMCMG++= abcOOBAcm.an.babcOAmanbpcdD'DOCABabcα Chia sẻ bởi:
GV. TRGV. TRGV. TRGV. TRẦẦẦẦN QUN QUN QUN QUỐỐỐỐC NGHC NGHC NGHC NGHĨAĨAĨAĨA 3333 IV.Điềukiệnđểbavéctơđồngphẳng①①①① Khái niện về sự đồng phẳng của ba véctơ trong không gian. Cho ba véctơ a, b, c (≠0) trong không gian. Từ một điểm O bất kì ta dựng OAa=, OBb=, OCc=. Khi đó xảy ra hai trường hợp: Các đường thẳng OA, OB, OC không cùng nằm trong một mặt phẳng thì ta nói ba véctơ a,b,c không đồng phẳng. Các đường thẳng OA, OB, OC cùng nằm trong một mặt phẳng thì ta nói ba véctơ a, b,c đồng phẳng. ②②②② Định nghĩa 3. Ba véctơ gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng. Trên hình bên, giá của các véctơ a, b, c cùng song song với mặt phẳng (α) nên ba véctơ a, b, c đồng phẳng. ③③③③ Điều kiện để ba véctơđồng phẳng Định lí 1.Cho ba véctơ a, b, c trong đó a và b không cùng phương. Điều kiện cần và đủ để ba véctơ a, b, c đồng phẳng là có duy nhất các sốm, n sao cho cmanb=+. ④④④④ Phân tích một véctơ theo ba véctơ không đồng phẳng Định lí 2. Nếu ba véctơ a, b, c không đồng phẳng thì với mỗi véctơ d, ta tìm được duy nhất các số m, n, p sao cho dmanbpc=++. Dạng1.TínhtoánvéctơA. PHƯƠNG PHÁP GIẢI ①①①①Quy tắc ba điểm: ABACCB=+ (quy tắc cộng) ABCBCA=− (quy tắc trừ) ②②②②Quy tắc hình bình hành: Với hình bình hành ABCD ta luôn có: ACABAD=+ ③③③③Quy tắc hình hộp: Cho hình hộp .ABCD ABCD′′′′, ta được: ACABADAA′′=++ ④④④④Quy tắc trung điểm: Cho I là trung điểm AB, M là điển bất kỳ: 0IAIB+= và 2MAMBMI+= ⑤⑤⑤⑤Tính chất trọng tâm của tam giác: G là trọng tâm ABC∆, M∀ ta có: 0GAGBGC++= và 3MAMBMCMG++= abcOOBAcm.an.babcOAmanbpcdD'DOCABabcα Chia sẻ bởi: Tải về
Liên kết tải về Chuyên đề vectơ trong không gian, quan hệ vuông góc 1,2 MB Tải về Tìm thêm: Toán 11Có thể bạn quan tâm
-

GDCD 7 Bài 2: Quan tâm, cảm thông và chia sẻ
10.000+ -

Đoạn văn Tiếng Anh về địa điểm du lịch (16 mẫu)
100.000+ 2 -

So sánh yếu tố kì ảo trong Chuyện chức phán sự đền Tản Viên của Nguyễn Dữ với truyện cổ tích Thạch Sanh
10.000+ -

Văn mẫu lớp 12: Nghị luận về cách vượt qua nghịch cảnh trong cuộc sống
100.000+ -

Văn mẫu lớp 7: Phân tích tình bạn qua bài Bạn đến chơi nhà (Dàn ý + 5 mẫu)
10.000+ -

Nghị luận về sự trải nghiệm trong cuộc sống
100.000+ 2 -

Bài thơ Đất nước (Nguyễn Đình Thi)
10.000+ -

Nghị luận về thói quen gây bè phái, chia rẽ tập thể lớp
10.000+ -

Phân tích đánh giá chủ đề và những nét đặc sắc về nghệ thuật của truyện Con chó xấu xí
10.000+ -

Chuyên đề giá trị tuyệt đối môn Toán lớp 7
10.000+
Nhiều người đang xem
Xác thực tài khoản!Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhấtHỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Hotline
024 322 333 96
Khiếu nại & Hoàn tiền
Giải quyết vấn đề đơn hàng & hoàn trả
Mới nhất trong tuần
-
Trả lời ngắn Toán 11: Phương trình lượng giác

-
Trắc nghiệm đúng sai Toán 11: Giới hạn của hàm số

-
Trắc nghiệm đúng sai Toán 11: Hàm số lượng giác

-
Trắc nghiệm đúng sai Toán 11: Quan hệ song song trong không gian

-
Trắc nghiệm đúng sai Toán 11: Phương trình lượng giác cơ bản

-
Trả lời ngắn Toán 11: Hàm số lượng giác

-
Trả lời ngắn Toán 11: Dãy số

-
Trả lời ngắn Toán 11: Góc lượng giác

-
Trả lời ngắn Toán 11: Giá trị lượng giác của góc lượng giác

-
Trả lời ngắn Toán 11: Công thức lượng giác

Tài khoản
Gói thành viên
Giới thiệu
Điều khoản
Bảo mật
Liên hệ
DMCA
Giấy phép số 569/GP-BTTTT. Bộ Thông tin và Truyền thông cấp ngày 30/08/2021. Cơ quan chủ quản: CÔNG TY CỔ PHẦN MẠNG TRỰC TUYẾN META. Địa chỉ: 56 Duy Tân, Phường Cầu Giấy, Hà Nội. Điện thoại: 024 2242 6188. Email: [email protected]. Bản quyền © 2025 download.vn.Từ khóa » Chuyên đề Vectơ Trong Không Gian
-
Chuyên đề Vectơ Trong Không Gian, Quan Hệ Vuông Góc
-
Chuyên đề Vecto Trong Không Gian Quan Hệ Vuông Góc
-
20 Dạng Bài Vectơ Trong Không Gian, Quan Hệ Vuông Góc Trong ...
-
Chuyên đề-vecto-trong-không Gian-quan Hệ-vuông Góc-lu-si-phap.pdf
-
Chuyên đề Vectơ Trong Không Gian Pps - Tài Liệu - 123doc
-
Chuyên đề Véctơ Trong Không Gian - Tài Liệu Text - 123doc
-
Hình Học 11 - Vecto Trong Không Gian- Đầy đủ Chi Tiết Nhất
-
Chuyên đề Hình Học 11 - Chương 3: Véc Tơ Trong Không Gian. Quan ...
-
Chuyên đề: Vectơ Trong Không Gian - Hình Học 11
-
Chuyên đề Vectơ Trong Không Gian, Quan Hệ Vuông Góc – Bản 1
-
Chuyên đề Vectơ Trong Không Gian, Quan Hệ Vuông Góc – Lư Sĩ Pháp
-
[PDF] Chuyên đề Vectơ Trong Không Gian, Quan Hệ Vuông Góc
-
Chuyên đề Vector Trong Không Gian, Quan Hệ Vuông Góc
-
Chuyên đề: Vectơ Trong Không Gian - Hình Học 11











