Công Thức Bán Kính Mặt Cầu

5/5 - (1 bình chọn)

Mục Lục

Toggle

• Định nghĩa mặt cầu ngoại tiếp
• Điều kiện cần và đủ để khối chóp có mặt cầu ngoại tiếp
• Công thức 1: Mặt cầu ngoại tiếp khối chóp có cạnh bên vuông góc với đáy
• Công thức 2: Khối tứ diện vuông (đây là trường hợp đặc biệt của công thức 1)
• Công thức 3: Khối lăng trụ đứng có đáy là đa giác nội tiếp (đây là trường hợp đặc biệt của công thức 1)
• Công thức 4: Công thức cho khối tứ diện có các đỉnh là đỉnh của một khối lăng trụ đứng
• Công thức 5: Công thức cho khối chóp có mặt
• Một số công thức tính bán kính mặt cầu
• Các dạng bài tập toán phương trình mặt cầu trong không gian Oxyz – toán lớp 12
• I. Lý thuyết về mặt cầu, phương trình mặt cầu
  • 1. Mặt cầu là gì?
  • 2. Các dạng phương trình mặt cầu
  • 3. Vị trí tương đối giữa mặt cầu và mặt phẳng
  • 4. Vị trí tương đối giữa mặt cầu và đường thẳng
  • 5. Đường tròn trong không gian Oxyz
• 6. Điều kiện tiếp xúc giữa đường thẳng với mặt cầu, mặt phẳng với mặt cầu
• II. Các dạng bài tập toán về phương trình mặt cầu
  • • Dạng 1: Viết phương trình mặt cầu biết tâm và bán kính
  • • Dạng 2: Vị trí tương đối giữa mặt cầu với mặt phẳng và đường thẳng
• Cách tìm tâm và bán kính mặt cầu
  • A. Phương pháp giải & Ví dụ
• Ví dụ minh họa
• B. Bài tập vận dụng
• Phương trình mặt cầu và các dạng bài tập
  • I. CÁC DẠNG PHƯƠNG TRÌNH MẶT CẦU
• II. DẠNG BÀI TẬP PHƯƠNG TRÌNH MẶT CẦU THƯỜNG GẶP
  • 1. NHẬN DẠNG PHƯƠNG TRÌΝH MẶT CẦU
  • 2. XÁC ĐỊNH TÂM VÀ BÁN KÍNH MẶT CẦU CÓ PHƯƠΝG TRÌNH TỔNG QUÁT
  • 3. VIẾT PHƯƠNG TRÌΝH MẶT CẦU ĐƯỜNG KÍNH AB
  • 4. VIẾT PHƯƠNG TRÌNH MẶT CẦU ĐI QUA 4 ĐIỂM
  • 5. VIẾT PHƯƠNG TRÌΝH MẶT CẦU CÓ TÂM I VÀ TIẾP XÚC VỚI ĐƯỜNG THẲNG
• Mặt cầu ngoại tiếp hình chóp | Công thức tính nhanh
  • I. TỔNG HỢP CÔNG THỨC TÍNH NHANH
  • II. CÁCH XÁC ĐỊNH TÂM MẶT CẦU NGOẠI TIẾP HÌNH CHÓP
  • III. HÌNH (KHỐI) CHÓP CÓ CÁC ĐỈNH CÙNG NHÌN MỘT CẠNH DƯỚI GÓC VUÔNG
• HÌNH (KHỐI) CHÓP ĐỀU
• IV. HÌNH CHÓP CÓ CẠNH BÊN VUÔNG GÓC VỚI ĐÁY
• V. MẶT CẦU NGOẠI TIẾP HÌNH CHÓP CÓ MẶT BÊN VUÔNG GÓC VỚI ĐÁY

Định nghĩa mặt cầu ngoại tiếp

• Mặt cầu ngoại tiếp khối đa diện là mặt cầu đi qua tất cả các đỉnh của khối đa diện đó

Điều kiện cần và đủ để khối chóp có mặt cầu ngoại tiếp

• Đáy là một đa giác nội tiếp

Công thức 1: Mặt cầu ngoại tiếp khối chóp có cạnh bên vuông góc với đáy

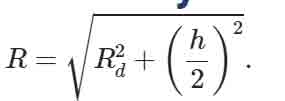
Trong đó RdRd là bán kính ngoại tiếp đáy; hh là độ dài cạnh bên vuông góc với đáy.

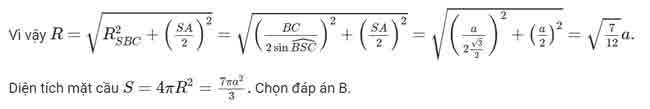
Công thức 2: Khối tứ diện vuông (đây là trường hợp đặc biệt của công thức 1)

Công thức 3: Khối lăng trụ đứng có đáy là đa giác nội tiếp (đây là trường hợp đặc biệt của công thức 1)

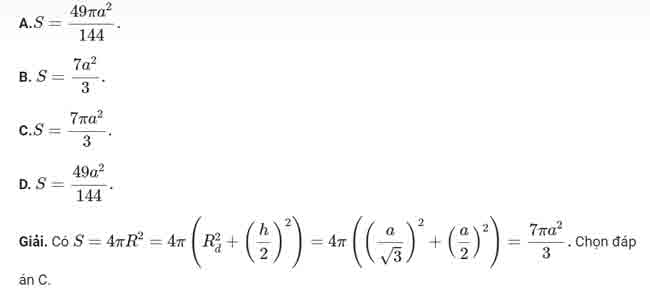
Công thức 4: Công thức cho khối tứ diện có các đỉnh là đỉnh của một khối lăng trụ đứng

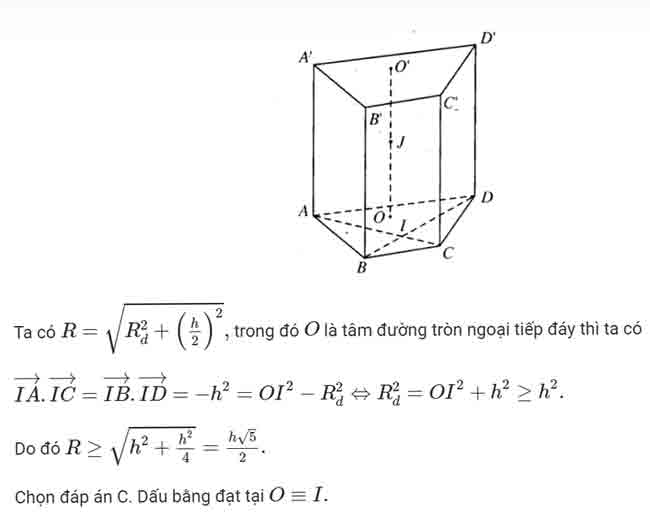
Công thức 5: Công thức cho khối chóp có mặt

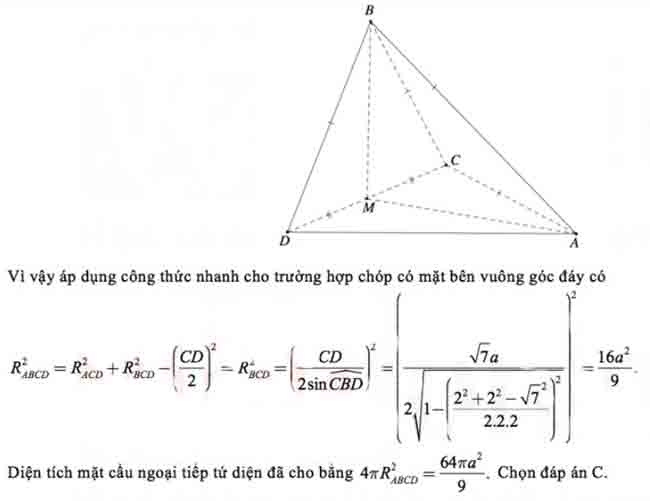
Một số công thức tính bán kính mặt cầu

Nhận xét 1. Xét hình chóp S.ABC, đường tròn ngoại tiếp tam giác ABC có tâm O và bán kính Rd. Gọi R là bán kính mặt cầu ngoại tiếp hình chóp S.ABC, ta có các trường hợp sau:

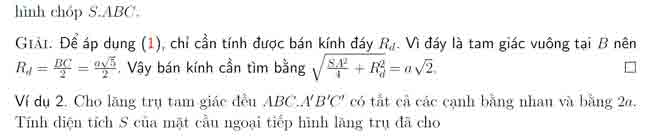
Các dạng bài tập toán phương trình mặt cầu trong không gian Oxyz – toán lớp 12

I. Lý thuyết về mặt cầu, phương trình mặt cầu

1. Mặt cầu là gì?

– Định nghĩa: Cho điểm O cố định và một số thực dương R. Tập hợp tất cả những điểm M trong không gian cách O một khoảng R được gọi là mặt cầu tâm O, bán kính R.

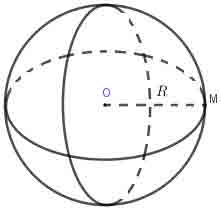
– Ký hiệu: S(O;R) ⇒ S(O;R) = {M/OM = R}

2. Các dạng phương trình mặt cầu

• Phương trình chính tắc của mặt cầu:

– Mặt cầu (S) có tâm O(a; b; c), bán kính R > 0 có pt là:

(S): (x – a)2 + (y – b)2 + (z – c)2 = R2

• Phương trình tổng quát của mặt cầu:

(S): x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0 (*)

◊ Điều kiện để phương trình (*) là phương trình mặt cầu: a2 + b2 + c2 – d > 0.

3. Vị trí tương đối giữa mặt cầu và mặt phẳng

• Cho mặt cầu S(O;R) và mặt phẳng (P). Gọi H là hình chiếu vuông góc của O lên (P) ⇒ d = OH là khoảng cách từ O đến mặt phẳng (P). Khi đó:

◊ Nếu d > R: Mặt cầu và mặt phẳng không có điểm chung

◊ Nếu d = R: Mặt phẳng tiếp xúc mặt cầu. Khi đó (P) là mặt phẳng tiếp diện của mặt cầu và H là tiếp điểm

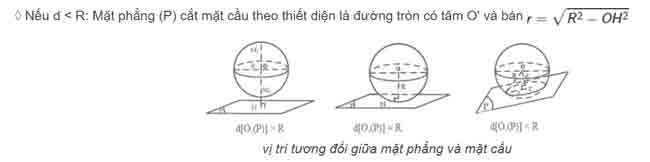
* Lưu ý: Khi mặt phẳng (P) đi qua tâm O thì mặt phẳng (P) được gọi là mặt phẳng kính và thiết diện lúc đó được gọi là đường tròn lớn có diện tích lớn nhất.

4. Vị trí tương đối giữa mặt cầu và đường thẳng

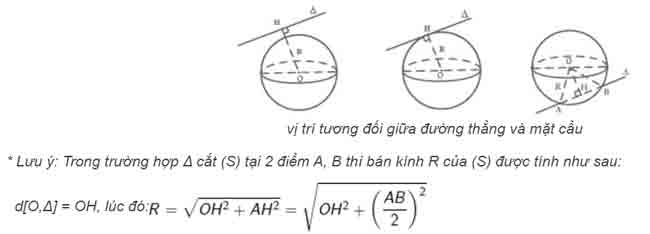
• Cho mặt cầu S(O;R) và đường thẳng Δ. Gọi H là hình chiếu của O lên Δ, khi đó :

◊ Nếu OH > R: Δ không cắt mặt cầu.

◊ Nếu OH = R: Δ tiếp xúc với mặt cầu. Khi đó Δ là tiếp tuyến của (S) và H là tiếp điểm.

◊ Nếu OH < R: Δ cắt mặt cầu tại hai điểm phân biệt.

5. Đường tròn trong không gian Oxyz

– Đường tròn (C) trong không gian Oxyz, được xem là giao tuyến của (S) và mặt phẳng (P).

(S): x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0

(P): Ax + By + Cz + D = 0

– Xác định tâm O’ và bán kính r của (C).

° Tâm O’ = d ∩ (P).

– Trong đó d là đường thẳng đi qua O và vuông góc với mp (P).

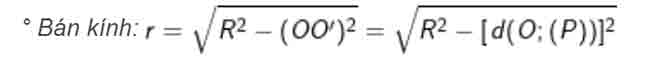
6. Điều kiện tiếp xúc giữa đường thẳng với mặt cầu, mặt phẳng với mặt cầu

+ Đường thẳng Δ là tiếp tuyến của mặt cầu (S)⇔ d[O;Δ] = R

+ Mặt phẳng (P) là tiếp diện của mặt cầu (S)⇔ d[O;(P)] = R

II. Các dạng bài tập toán về phương trình mặt cầu

• Dạng 1: Viết phương trình mặt cầu biết tâm và bán kính

* Phương pháp:

+) Cách 1: Viết PT mặt cầu dạng chính tắc

Bước 1: Xác định tâm O(a; b; c).

Bước 2: Xác định bán kính R của (S).

Bước 3: Mặt cầu (S) có tâm O(a; b; c) và bán kính R là:

(S): (x – a)2 + (y – b)2 + (z – c)2 = R2

+) Cách 2: Viết phương trình mặt cầu dạng tổng quát

– Gọi phương trình (S) : x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0

– Phương trình (S) hoàn toàn xác định nếu biết được a,b,c,d với a2 + b2 + c2 – d > 0.

* Ví dụ 1: Viết phương trình mặt cầu (S), trong các trường hợp sau:

1. (S) có tâm O(2; 2; -3) và bán kính R = 3.

2. (S) có tâm O(1; 2; 0) và (S) qua P(2; -2; 1)

3. (S) có đường kính AB với A(1; 3; 1) và B(-2; 0; 1)

* Lời giải:

1. (S) có tâm O(2; 2; -3) và bán kính R = 3. có phương trình là:

(x – 2)2 + (y – 2)2 + (z + 3)2 = 9

2. (S) có tâm O(1; 2; 0) và (S) qua P(2; -2; 1)

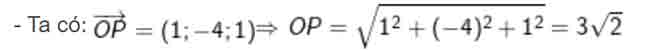
– Mặt cầu tâm O(1; 2; 0) bán kính R = OP = 3√2 có phương trình:

(x – 1)2 + (y – 2)2 + z2 = 18

3. (S) có đường kính AB với A(1; 3; 1) và B(-2; 0; 1)

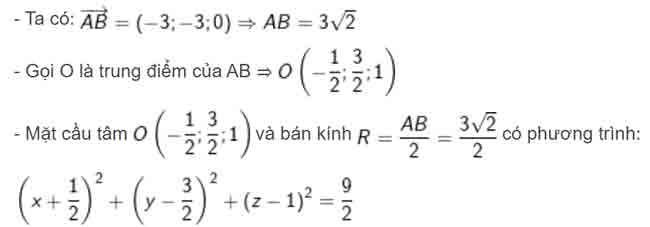
* Ví dụ 2: Viết phương trình mặt cầu (S) , trong các trường hợp sau:

1. (S) qua A(3; 1; 0) , B(5; 5; 0) và tâm I thuộc trục Ox.

2. (S) có tâm O và tiếp xúc mặt phẳng (P): 16x – 15y – 12z + 75 = 0

* Ví dụ 3: Viết phương trình mặt cầu (S) biết :

1. (S) qua bốn điểm A(1; 2; -4), B(1; -3; 1) , C(2; 2; 3) và D(1; 0 ; 4)

2. (S) qua A(0; 8; 0), B(4; 6; 2) , C(0; 12; 4) và có tâm I thuộc mp (Oyz)

* Lời giải:

a) Có thể giải theo 2 cách:

* Cách 1: Viết pt mặt cầu dạng chính tắc

– Gọi I(a;b;c) là tâm mặt cầu cần tìm, theo giả thiết ta có:

x2 + (y – 7)2 + (z – 5)2 = 26.

• Dạng 2: Vị trí tương đối giữa mặt cầu với mặt phẳng và đường thẳng

* Phương pháp:

– Sử dụng các công thức liên quan về vị trí tương đối giữa đường thẳng, mặt phẳng mặt cầu:

+ Đường thẳng Δ là tiếp tuyến của mặt cầu (S)⇔ d[O;Δ] = R

+ Mặt phẳng (P) là tiếp diện của mặt cầu (S)⇔ d[O;(P)] = R

* Lời giải:

a) Viết phương trình mặt cầu tâm I và tiếp xúc với trục Oy.

– Gọi M là hình chiếu của I(1;-2;3) lên Oy, ta có M(0;-2;0)

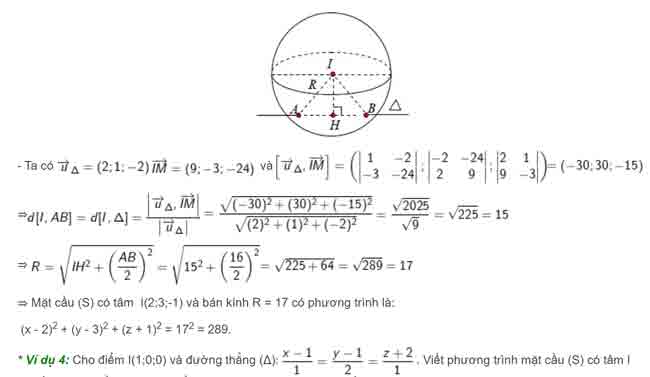
và cắt đường thẳng (Δ) tại 2 điểm A, B sao cho tam giác IAB đều.

* Lời giải:

Cách tìm tâm và bán kính mặt cầu

A. Phương pháp giải & Ví dụ

+ Phương trình (S): (x-a)2+(y-b)2+(z-c)2=R2 là phương trình mặt cầu (S) có tâm I (a; b; c), bán kính R

+ Phương trình (S): x2+y2+z2-2ax-2by-2cz+d=0 thỏa mãn điều kiện a2+b2+c2-d>0 là phương trình mặt cầu tâm I (a; b; c); bán kính

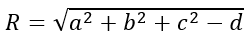
Ví dụ minh họa

Bài 1: Trong không gian hệ trục tọa độ Oxyz, phương trình nào sau đây là phương trình mặt cầu, nếu là phương trình mặt cầu, hãy tìm tâm và bán kính của mặt cầu đó

a) (x-2)2+(y+3)2+z2=5

b) x2+y2+z2-2x+4y-6z+1=0

c) 3x2+3y2+3z2-6x+3y+21=0

Hướng dẫn:

a) Phương trình (x-2)2+(y+3)2+z2=5 có dạng

(x-a)2+(y-b)2+(z-c)2=R2 nên là phương trình mặt cầu có tâm

I (2; -3; 0) và bán kính R=√5.

b) Phương trình x2+y2+z2-2x+4y-6z+1=0 có dạng

x2+y2+z2-2ax-2by-2cz+d=0 với a = 1; b = -2; c = 3, d = 1

⇒ a2+b2+c2-d=13>0

Vậy phương trình đã cho là phương trình mặt cầu có tâm I (1; -2; 3) và bán kính R=√13.

c) Phương trình 3x2+3y2+3z2-6x+3y+21=0

⇔ x2+y2+z2-2x+y+7=0

Phương trình có dạng x2+y2+z2-2ax-2by-2cz+d=0 với

a=1;b=(-1)/2;c=0;d=7 ⇒a2+b2+c2-d=(-23)/4<0

Vậy phương trình đã cho không phải là phương trình mặt cầu.

Bài 2: Trong không gian với hệ tọa độ Oxyz, tìm m để mỗi phương trình sau là phương trình mặt cầu.

a) x2+y2+z2-2mx+2(m+1)y-4z+1=0

b) x2+y2+z2-2(m-3)x-4mz+8=0

Hướng dẫn:

a) Phương trình x2+y2+z2-2mx+2(m+1)y-4z+1=0 có

a=m;b=-(m+1); c=2;d=1.

Phương trình là phương trình mặt cầu ⇔ a2+b2+c2-d>0

⇔ m2+(m+1)2+22-1>0⇔2m2+2m+3>0 ⇔m∈R.

b) Phương trình x2+y2+z2-2(m-3)x-4mz+8=0 có a=m-3;

b=0;c=2m;d=8

Phương trình là phương trình mặt cầu ⇔a2+b2+c2-d>0

⇔(m-3)2+4m2-8>0 ⇔5m2-6m+1>0

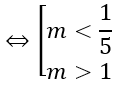
Bài 3: Trong không gian hệ trục tọa độ Oxyz, tìm tất cả các giá trị thực của tham số m để phương trình x2+y2+z2+2(m+2)x-2(m-3)z+m2-1=0 là phương trình của mặt cầu có bán kính nhỏ nhất.

Hướng dẫn:

Phương trình x2+y2+z2+2(m+2)x-2(m-3)z+m2-1=0 có:

a=-(m+2);b=0;c=m-3;d=m2-1

Phương trình là phương trình mặt cầu ⇔ a2+b2+c2-d>0

⇔ (m+2)2+(m-3)2-m2+1>0 ⇔ m2-2m+14>0 ⇔ m∈R.

Khi đó, bán kính mặt cầu là:

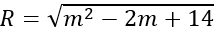
Dấu bằng xảy ra khi m = 1.

Vậy với m = 1 thì mặt cầu có bán kính nhỏ nhất R=√13.

B. Bài tập vận dụng

Bài 1: Phương trình nào sau đây là phương trình mặt cầu ?

A. x2+y2+z2-2x=0

B. x2+y2 – z2+2x-y+1=0

C. 2x2+2y2 = (x+y)2 – z2+2x-1

D. (x+y)2 = 2xy – z2 – 1

Đáp án : A

Giải thích :

Phương trình x2+y2+z2-2ax-2by-2cz+d=0 là phương trình mặt cầu ⇔ a2+b2+c2-d>0

Bài 2: Phương trình nào sau đây không phải là phương trình mặt cầu?

A. x2 + y2 + z2 + 2x – 2y + 1 = 0.

B. x2 + y2 + z2 – 2x = 0.

C. 2x2 + 2y2 = (x + y)2 – z2 + 2x – 1.

D. ( x + y)2 = 2xy – z2 + 1 – 4x.

Đáp án : C

Bài 3: Cho các phương trình sau:

( x – 1)2 + y2 + z2 = 1

x2 + ( 2y – 1)2+ z2 = 4

x2 + y2 + z2 + 1 = 0

( 2x + 1)2+ ( 2y – 1)2 + 4z2 = 16

Số phương trình là phương trình mặt cầu là:

A. 1 B. 3

C. 4 D. 2

Đáp án : D

Giải thích :

Các phương trình mặt cầu là:

( x – 1)2 + y2 + z2 = 1

x2 + ( 2y – 1)2 + z2 = 4

Bài 4: Mặt cầu ( S ): x2+ y2+ z2– 2x + 10y + 3z + 1 = 0 đi qua điểm có tọa độ nào sau đây?

A. (3; – 2; – 4) B. ( 2;1;9)

C. ( 4; – 1;0) D.(- 1;3; – 1)

Đáp án : B

Giải thích :

Thử trực tiếp đáp án, điểm (2; 1; 9) thỏa mãn phương trình mặt cầu.

Bài 5: Mặt cầu ( S ): x2+ y2 + z2 – 4x + 1 = 0 có tọa độ tâm và bán kính R là:

A. I(-2;0;0), R = √3

B. I(2;0;0), R = √3

C. I(0;2;0), R = √3

D. I(2;0;0), R = 3

Đáp án : B

Giải thích :

( S ): x2 + y2 + z2– 4x + 1 = 0

⇔ (x-2)2+y2+z2=3

Phương trình có tâm I (2 ; 0 ; 0), bán kính R=√3

Bài 6: Phương trình mặt cầu có tâm I(-1;2;3), bán kình R=3 là:

A. (x + 1)2+ ( y – 2)2 + ( z + 3)2 = 9

B. ( x + 1)2+ ( y – 2)2+ ( z + 3)2 = 3

C. ( x – 1)2+ ( y + 2)2 + ( z – 3)2 = 9

D. ( x + 1)2+ ( y – 2)2+ ( z + 3)2 = 9

Đáp án : A

Giải thích :

Phương trình mặt cầu tâm I (a; b; c), bán kính R là:

(x-a)2+(y-b)2+(z-c)2=R2

Bài 7: Mặt cầu ( S ): ( x + y)2= 2xy – z2 + 1 – 4x có tâm là:

A. I(2;0;0) B. I(4;0;0)

C. I(-4;0;0) D. I(-2;0;0)

Đáp án : D

Giải thích :

(x+y)2=2xy-z2+1-4x ⇔ x2+y2+z2+4x=1

Phương trình có a=-2;b=0;c=0 ⇒ I(-2;0;0)

Bài 8: Mặt cầu có phương trình nào sau đây có tâm là I(-1;1;0) ?

A. x2+ y2 + z2+ 2x – 2y + 1 = 0.

B. x2 + y2+ z2 – 2x + 2y = 0.

C. 2x2 + 2y2 = ( x + y)2 – z2+ 2x – 1 – 2xy.

D. ( x + y)2 = 2xy – z2+ 1 – 4x.

Đáp án : A

Giải thích :

A. x2+ y2 + z2 + 2x – 2y + 1 = 0.

⇔ (x+1)2+(y-1)2+z2=1

Phương trình có tâm I (-1 ; 1 ; 0), bán kính R =1

B. x2 + y2 + z2 – 2x + 2y = 0.

⇔ (x-1)2+(y+1)2+z2=2

Phương trình có tâm I (1 ; -1 ; 0), bán kính R=√2

C.2x2+ 2y2= ( x + y )2 – z2 + 2x – 1 – 2xy.

⇔ x2+y2+z2-2x+1=0

⇔ (x-1)2+y2+z2=0

Đây không phải là phương trình mặt cầu.

D. (x + y)2= 2xy – z2+ 1 – 4x.

⇔ x2+y2+z2+4x-1=0

⇔(x+2)2+y2+z2=5

Phương trình có tâm I (-2 ; 0 ; 0), bán kính R=√5

Bài 9: Gọi I là tâm mặt cầu ( S ): x2 + y2 + ( z – 2)2= 4. Độ dài OI→ (O là gốc tọa độ) bằng?

A. 1 B. 4

C. 2 D. √2

Đáp án : C

Giải thích :

Mặt cầu ( S ): x2 + y2 + ( z – 2)2= 4 có tâm I (0; 0; 2) ⇒ OI=2

Bài 10: Phương trình mặt cầu có bán kính bằng 3 và tâm là giao điểm của ba trục toạ độ ?

A. x2+ y2 + z2 – 6x = 0.

B. x2 + y2 + z2 – 6y = 0.

C. x2 + y2 + z2 – 6z = 0.

D. x2 + y2 + z2 = 9.

Đáp án : D

Giải thích :

Giao điểm của 3 trục tọa độ là điểm O (0; 0; 0)

Khi đó, phương trình mặt cầu có tâm O (0; 0; 0) và bán kính R = 3 là

x2+y2+z2=9

Phương trình mặt cầu và các dạng bài tập

I. CÁC DẠNG PHƯƠNG TRÌNH MẶT CẦU

Trước tiên ta cần nhắc lại khái niệm mặt cầu là gì? Trong không gian, mặt cầu là quỹ tích các điểm cách đều một điểm cho trước một khoảng không đổi. Khoảng không đổi đó gọi là bán kính. Điểm cho trước gọi là tâm mặt cầu.

Mặt cầu cũng có thể được định nghĩa theo khái niệm mặt tròn xoay. Theo đó mặt cầu là mặt tròn xoay khi quay đường tròn quanh một đường kính.

Trong không gian Oxyz cho mặt cầu S tâm I(a;b;c) bán kính R. Phương trình chính tắc của (S) là:

(x-a)²+(y-b)²+(z-c)²=R²

Ngoài ra nếu a²+b²+c²-d>0 thì phương trình sau đây là phương trình tổng quát của (S):

x²+y²+z²-2ax-2by-2cz+d=0 (1)

Tọa độ tâm của (S) có phương trình (1) là I(a;b;c) và bán kính của (S) được tính theo công thức:

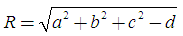
II. DẠNG BÀI TẬP PHƯƠNG TRÌNH MẶT CẦU THƯỜNG GẶP

1. NHẬN DẠNG PHƯƠNG TRÌΝH MẶT CẦU

Với dạng toán này, chúng ta có 1 số phương trình. Và được yêu cầu nhận dạng xem phương trình nào là phương trình của một mặt câ`u.

Ví dụ minh họa:

Phương trình nào dưới đây là phương trình mặt câ`u?

A. x²+y²+z²-4x+6y+2z+14=0.

B. x²+y²+z²-8x+2y+2z+62=0.

C. 3x²+y²+2z²-4x+6y+2z-6=0.

D. x²+y²+z²-4x+8y+2z-6=0.

Lời giải:

Đối với dạng toán này chúng ta cần lưu ý 1 số điểm như:

• Hệ số của x², y², z² phải giống nhau. Nếu hệ số của x², y², z² giống nhau mà chưa bằng 1 thì ta chia cả 2 vế phương trình để hệ số của x², y², z² bằng 1.

Phương trình x²+y²+z²-2ax-2by-2cz+d=0 muốn là phương trình mặt câ`u thì a²+b²+c²-d>0 (điều kiện để có phương trình mặt cầu).

Trong ví dụ trên, phương án A không thỏa mãn vì a²+b²+c²-d=2²+(-3)²+(-1)²-14=0.

Phương án B không thỏa mãn vì a²+b²+c²-d=4²+(-1)²+(-1)²-62<0.

Phương án C không thỏa mãn vì hệ số của x², y², z² không bằng nhau.

Phương án D là đáp án đúng vì a²+b²+c²-d=2²+(-4)²+(-1)²+6=27>0.

Chọn đáp án D.

2. XÁC ĐỊNH TÂM VÀ BÁN KÍNH MẶT CẦU CÓ PHƯƠΝG TRÌNH TỔNG QUÁT

Ví dụ minh họa:

Trong không gian Oxyz, mặt cầu (S): 2x²+2y²+2z²-8x+8y-4z=0 có tâm và bán kính lần lượt là

A. I(-2;2;-1), R=3.

B. I(2;-2;1), R=3.

C. I(-2;2;-1), R=9.

D. I(2;-2;1), R=9.

Lời giải+Hướng dẫn:

Trước hết, chúng ta cần kiểm tra hệ số của x², y², z² nếu khác 1 thì cần chia cả 2 vế cho số phù hợp. Ở bài này chúng ta chia cả 2 vế của phương trình cho 2 ta được (S): x²+y²+z²-4x+4y-2z=0.

Tiếp theo để xác định tọa độ tâm mặt cầu chúng ta lấy hệ số của x, y, z chia cho -2 ta được: I(2;-2;1).

Để xác định bán kính mặt cầu ta lấy tổng bình phương các tọa độ của tâm trừ hệ số tự do được kết quả bao nhiêu thì lấy căn bậc 2.

Bán kính mặt cầu là R²=2²+(-2)²+1²-0=9⇒R=3. Chọn đáp án B.

3. VIẾT PHƯƠNG TRÌΝH MẶT CẦU ĐƯỜNG KÍNH AB

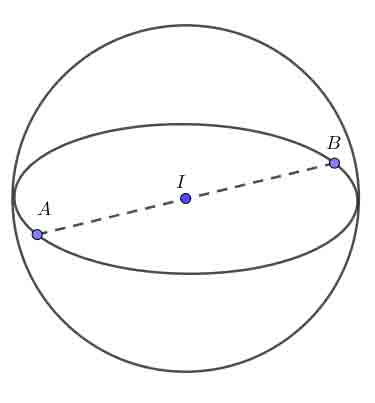
Để làm dạng toán này ta xác định tâm là trung điểm AB, bán kính bằng nửa độ dài AB.

Ví dụ minh họa:

Trong không gian Oxyz, cho điểm A(1;2;3) và điểm B(5;2;-1). Viết phương trình mặt cầu đường kính AB.

A. (x-3)²+(y-2)²+(z-1)²=32.

B. (x+3)²+(y+2)²+(z+1)²=8.

C. (x+3)²+(y+2)²+(z+1)²=32.

D.(x-3)²+(y-2)²+(z-1)²=8.

Lời giải:

Tâm mặt cầu là trung điểm AB và có tọa độ là: I(3;2;1).

Gọi R là bán kính mặt cầu, ta có: (2R)²=(5-1)²+(2-2)²+(-1-3)²=32⇒R²=8.

Vậy công thức phương trình mặt cầu cần tìm là: (x-3)²+(y-2)²+(z-1)²=8.

Chọn đáp án D.

4. VIẾT PHƯƠNG TRÌNH MẶT CẦU ĐI QUA 4 ĐIỂM

Có nhiều cách để giải dạng toán này. Trong đó cách làm nhanh hơn là thay tọa độ 4 điểm vào dạng phương trình tổng quát. Sau đó dùng máy tính bỏ túi giải hệ 4 phương trình 4 ẩn.

Ví dụ minh họa (Tự luận):

Trong không gian Oxyz, cho 4 điểm A(-1;-1;-1), B(1;0;0), C(0;2;0), D(0;0;3). Mặt câ`u (S) đi qua 4 điểm A, B, C, D có phương trình là gì?

Lời giải:

5. VIẾT PHƯƠNG TRÌΝH MẶT CẦU CÓ TÂM I VÀ TIẾP XÚC VỚI ĐƯỜNG THẲNG

Có duy nhất một mặt cầu tâm I tiếp xúc với đường thẳng d. Bán kính R của mặt cầu này chính là khoảng cách từ I đến d.

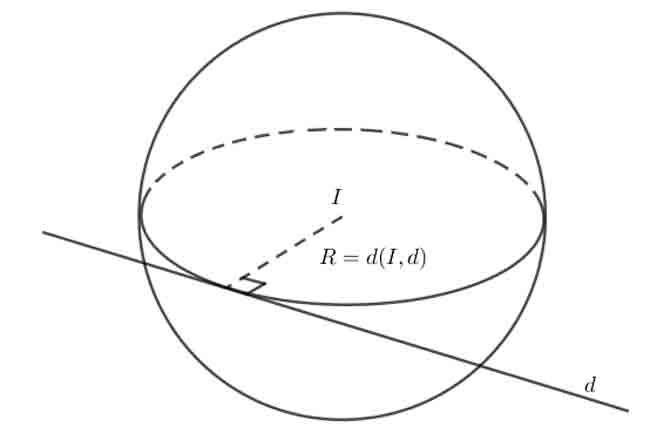
Ví dụ minh họa (Tự luận):

Trong không gian Oxyz, cho điểm I(2;-1;3). Phương trình mặt cầu tâm I tiếp xúc với trục Oy là gì?

Lời giải:

Bán kính mặt cầu là khoảng cách từ I tới trục Oy: R=|-1|=1.

(Mẹo: Chiếu lên trục nào thì lấy trị tuyệt đối cái đó, ví dụ ở đây chiếu lên trục Oy thì ta chỉ cần lấy trị tuyệt đối của tung độ).

Vậy phương trình mặt cầu tiếp xúc với trục Oy cần tìm là : (x-2)²+(y+1)²+(z-3)²=1.

Mặt cầu ngoại tiếp hình chóp | Công thức tính nhanh

I. TỔNG HỢP CÔNG THỨC TÍNH NHANH

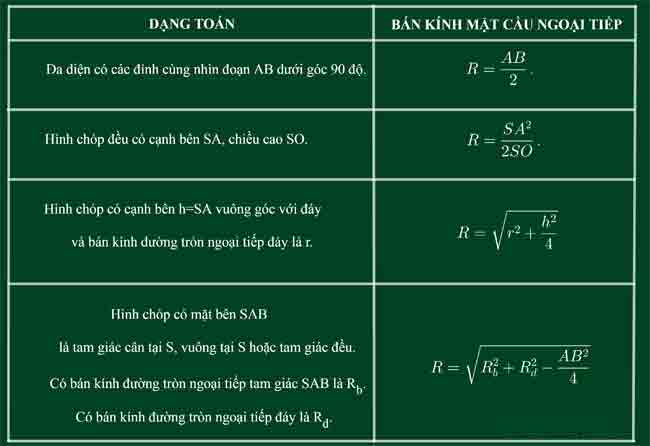
II. CÁCH XÁC ĐỊNH TÂM MẶT CẦU NGOẠI TIẾP HÌNH CHÓP

Để xác định tâm mặt cầu ngoại tiếp hình chóp ta thực hiện theo các bước sau:

Bước 1: Xác định trục của đường tròn ngoại tiếp đa giác đáy. Gọi tắt là trục của đáy ( là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).Bước 2: Xác định mặt phẳng trung trực của một cạnh bên. Hoặc trục của của đường tròn ngoại tiếp một đa giác của mặt bên.Bước 3: Giao điểm của trục của đáy và mặt phẳng trung trực của một cạnh bên (hoặc trục của đáy của và trục của một mặt bên) là tâm mặt cầu ngoại tiếp.Nhận xét: Hình chóp có đáy hoặc các mặt bên là các đa giác không nội tiếp được đường tròn thì hình chóp đó không nội tiếp được mặt cầu.

III. HÌNH (KHỐI) CHÓP CÓ CÁC ĐỈNH CÙNG NHÌN MỘT CẠNH DƯỚI GÓC VUÔNG

Nếu khối chóp có các đỉnh cùng nhìn 1 cạnh AB (Các đỉnh không nằm trên cạnh đó-Không kể A, B) thì tâm mặt cầu ngoại tiếp khối chóp đó là trung điểm AB. Đồng thời AB là đường kính mặt cầu. Bán kính R=AB/2.

Ví dụ:

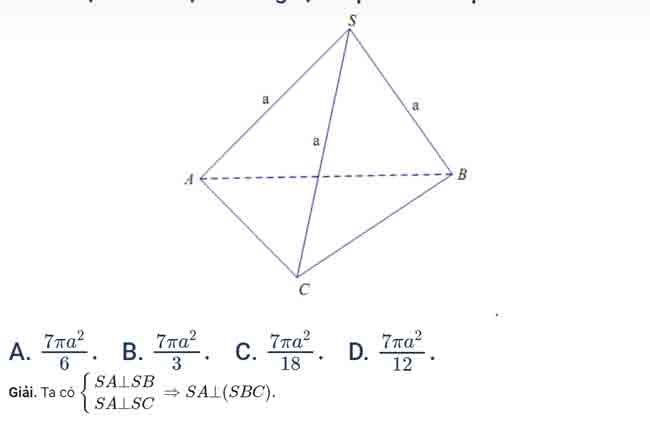
Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy. Đáy là tam giác vuông tại B. Tính thể tích khối cầu ngoại tiếp khối chóp S.ABC biết SC=2a.

Lời giải:

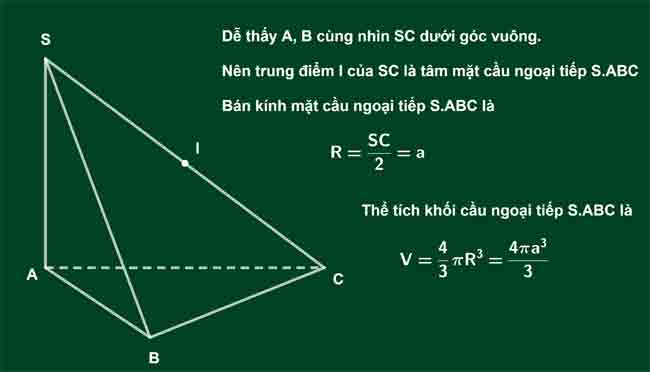
HÌNH (KHỐI) CHÓP ĐỀU

Khối chóp đều có cạnh bên SA và chiều cao SO thì bán kính mặt cầu ngoại tiếp khối chóp là

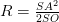
Chứng minh:

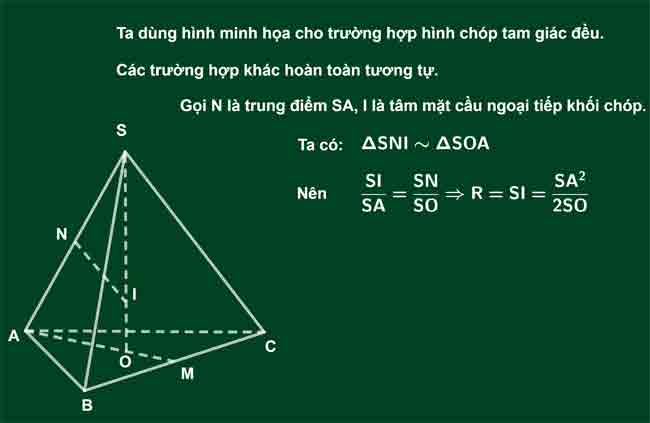
Ví dụ:

Biết tứ diện đều cạnh a nội tiếp mặt cầu (S) bán kính R. Tính R.

Lời giải:

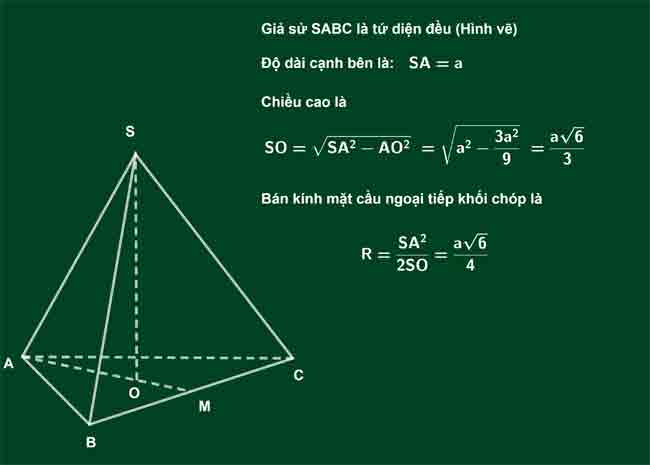
IV. HÌNH CHÓP CÓ CẠNH BÊN VUÔNG GÓC VỚI ĐÁY

Hình chóp có cạnh bên SA=h vuông góc với đáy và có bán kính đường tròn ngoại tiếp đáy là r. Bán kính khối cầu ngoại tiếp hình chóp đó là

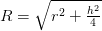
Chứng minh:

V. MẶT CẦU NGOẠI TIẾP HÌNH CHÓP CÓ MẶT BÊN VUÔNG GÓC VỚI ĐÁY

Giả sử hình chóp có mặt bên SAB là tam giác đều, cân tại S, vuông tại S và đồng thời nằm trong mặt phẳng vuông góc với đáy. Gọi Rb là bán kính đường tròn ngoại tiếp tam giác SAB. Gọi Rd là bán kính đường tròn ngoại tiếp đáy. Bán kính khối cầu ngoại tiếp hình chóp đó là

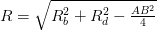
Công thức toán

Gia sư môn toán

Công thức tính diện tích mặt cầu

Công thức bán kính mặt cầu

Công thức Bernoulli