Công Thức, Cách Tính Diện Tích Mặt Cầu Và Thể Tích Khối Cầu, Bài Tập ...
Có thể bạn quan tâm
Vậy công thức và cách tính diện tích mặt cầu, thể tích của khối cầu được viết như thế nào? Nội dung bài viết này chúng ta cùng ôn lại các công thức tính này và vận dụng vào các bài tập minh họa cụ thể.
» Đừng bỏ lỡ: Các dạng toán phương trình mặt cầu trong không gian Oxyz cực hay
I. Công thức tính diện tích mặt cầu và thể tích khối cầu
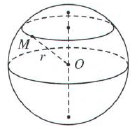
1. Công thức tính diện tính mặt cầu
- Mặt cầu có bán kính r có diện tích là:
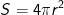
2. Công thức tính thể tích khối cầu
- Khối cầu có bán kính r có thể tích là:
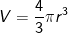
> Chú ý: - Diện tích S của mặt cầu bán kính r bằng 4 lần diện tích hình tròn lớn nhất của mặt cầu đó.
- Thể tích V của khối cầu bán kính r bằng thể tích khối chóp có diện tích đáy bằng diện tích mặt cầu và có chiều cao bằng bán kính của khối cầu đó.
II. Bài tập vận dụng tính diện tích mặt cầu và Thể tính khối cầu
* Bài 1 (Bài 10 trang 49 SGK Hình học 12): Cho hình chóp S.ABC có bốn đỉnh đều nằm trên một mặt cầu, SA = a, SB = b, SC = c và ba cạnh SA, SB, SC đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.
* Lời giải:
- Minh họa hình như sau: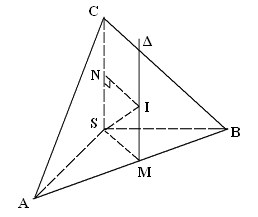 - Ta gọi M là trung điểm của cạnh AB.
- Ta gọi M là trung điểm của cạnh AB.
- Ta có, ΔSAB là tam giác vuông tại S có SM là đường trung tuyến nên:
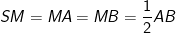
⇒ M là tâm đường tròn ngoại tiếp tam giác SAB.
- Kẻ đường thẳng Δ qua M và vuông góc với mp(SAB), khi đó ta có:
Δ//SC và Δ là trục đường tròn ngoại tiếp ΔSAB.
- Trong mp(Δ,SC), đường trung trực của SC cắt Δ tại điểm I.
- Ta có: IS = IC. (1)
và IS = IB = IA (2).
Từ (1) và (2) suy ra: IA = IB= IC = IS
⇒ I là tâm mặt cầu ngoại tiếp hình chóp S.ABC
- Bán kính mặt cầu ngoại tiếp hình chóp là:
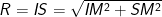 với
với
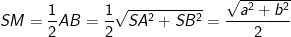
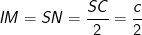
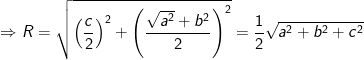
- Diện tích mặt cầu là:
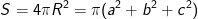
- Thể tích khối cầu là:
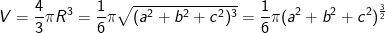
* Bài 2 (Bài 6 trang 50 SGK Hình học 12): Cho hình vuông ABCD cạnh a. Từ tâm O của hình vuông dựng đường thẳng Δ vuông góc với mặt phẳng (ABCD). Trên Δ lấy điểm S sao cho OS = a/2 . Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.
* Lời giải:
- Hình minh họa như sau: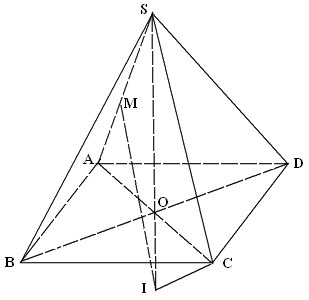
- Giả sử Δ là trục của hình vuông ABCD, vậy tâm I của mặt cầu ngoại tiếp hình chóp S.ABCD nằm trên Δ.
- ABCD là hình vuông cạnh a nên ta có:
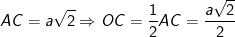
- Vì SO = a/2 < OC nên tâm I của mặt cầu phải nằm trên phần kéo dài SO.
- Ta có: 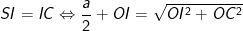
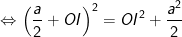
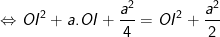
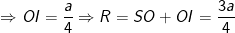
- Vậy tâm I của mặt cầu ngoại tiếp hình chóp S.ABCD nằm trên SO mà SI = R = 31/4; (R là bán kính hình cầu), khi đó:
- Diện tích mặt cầu là: 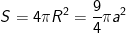
- Thể tích khối cầu là: 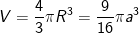
* Bài 3 (Bài 3 trang 51 SGK Hình học 12): Hình chóp S.ABC có đáy là tam giác ABC vuông tại A, SA vuông góc với mặt phẳng (ABC) và SA = a, AB = b, AC = c. Mặt cầu đi qua các đỉnh A, B, C, S có bán kính r bằng bao nhiêu?
* Lời giải:
- Hình minh họa như sau: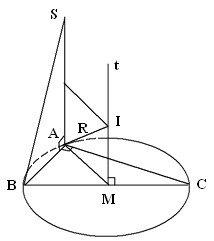
- Gọi M là trung điểm của BC, khi đó MC = MB = MA ⇒ M là tâm đường tròn ngoại tiếp ΔABC.
- Dựng Mt ⊥ (ABC) ta có: Mt//SA và Mt là trục đường tròn ngoại tiếp ΔABC
- Trong mp(SA,Mt) đường trung trực của SA cắt Mt tại I, ta có:
IS = IA và IA = IB = IC
⇒ IS = IA = IB = IC
⇒ I là tâm mặt cầu ngoại tiếp tứ diện S.ABC
- Bán kính mặt cầu: 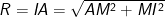 , với
, với
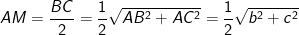
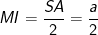
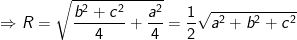
Đến đây nếu muốn tính diện tích mặt cầu tâm I bán kính R hay thể tích mặt cầu tâm I bán kính R ta chỉ việc vận dụng công thức là ra kết quả.
Từ khóa » Tổng Hợp Công Thức Thể Tích Mặt Cầu
-
Công Thức Tính Thể Tích Khối Cầu (hình Cầu) Đầy Đủ & Chính Xác Nhất
-
Công Thức Tính Diện Tích Mặt Cầu, Thể Tích Khối Cầu
-
Thể Tích Và Diện Tích Hình Cầu - Phép Tính Online
-
[2] Công Thức Tính Thể Tích Khối Cầu, Diện Tích Mặt Cầu
-
[] - Tổng Hợp Tất Cả Các Công Thức Tính Nhanh Bán Kính Mặt ...
-
Công Thức Diện Tích Mặt Cầu, Thể Tích Hình Cầu | DBK Việt Nam
-
Công Thức Tính Thể Tích Khối Cầu Nhanh Và Chính Xác Nhất
-
Mặt Cầu Là Gì ? Công Thức Diện Tích Mặt Cầu, Thể Tích Khối Cầu
-
Cách Tính Thể Tích Khối Cầu (Hình Cầu) - Từ Điển Toán Học
-
Công Thức Tính Thể Tích Khối Cầu Và Bài Tập Có Lời Giải Từ A - Z
-
Cách Tính Thể Tích Hình Cầu, Diện Tích Mặt Cầu, Công Thức Tính
-
[2] Công Thức Tính Thể Tích Khối Cầu, Diện Tích Mặt Cầu
-
Khối Cầu Là Gì? Công Thức Giải Nhanh, Thể Tích, Vị Trí Tương đối
-
Tổng Hợp Các Công Thức Tính Thể Tích, Diện Tích Hình Cầu Bất Kỳ